Теорема о сумме углов треугольника

ПЛАН-КОНСПЕКТ УРОКА Дата урока: 12.02. 2019г.

Предмет: алгебра 7 класс Учитель математики: Рыжакова А.А

Тема урока: ТЕОРЕМА О СУММЕ УГЛОВ ТРЕУГОЛЬНИКА

Цели урока: доказать теорему о сумме углов треугольника, следствия из нее; ввести понятия остроугольного, прямоугольного и тупоугольного треугольников; рассмотреть задачи на применение доказанных утверждений.

Задачи урока:

• доказать теорему о сумме углов треугольника, показать применение нового материала при работе с тестами.

• способствовать формированию логического мышления, интеллектуальных навыков, обобщения, умения выделять главное, ставить перед собой вопросы, развитию исследовательских умений учащихся способствовать развитию стремления выдвигать гипотезу и доказывать ее.

• : способствовать воспитанию математической грамотности; формированию коммуникативных качеств личности (сотрудничество, умение выслушать собеседника и высказать свою точку зрения).

Планируемые результаты урока:

Формирование УУД:

Предметные:

Познакомиться с понятием внешний угол треугольника. Научиться формулировать теоремы о сумме углов треугольника с доказательством, ее следствия, называть свойство внешнего угла треугольника и применять его на практике, решать простейшие задачи по теме

Метапредметные:

Коммуникативные: слушать и слышать собеседника, вступать с ним в учебный диалог.

Регулятивные: сличать способ и результат своих действий с заданным эталоном, обнаруживать отклонения и отличия от эталона.

Познавательные: передавать основное содержание в сжатом, выборочном или развернутом виде

Личностные:

Формирование навыков самоанализа и самоконтроля

Тип урока Урок контроля знаний и умений

Оборудование: мел, доска, раздаточный материал

Ход урока

I.  Анализ результатов контрольной работы.

1. Проанализировать характерные ошибки, допущенные в контрольной работе.

2. Выполнить работу над ошибками.

 II. Изучение нового материала.

1. Решить задачу по готовому чертежу на доске (см. рис.).

На рисунке ВД || АС.

Найдите сумму углов треугольника ABC.

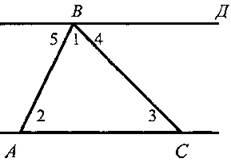
 2. Вслед за решением этой задачи перед учащимися ставится вопрос: случайно ли сумма углов данного треугольника ABC оказалась равной 180° или этим свойством обладает любой треугольник?

Поиск ответа естественно приводит к формированию теоремы о сумме углов треугольника.

3. Доказательство теоремы о сумме углов треугольника (рис. 124 учебника).

4. Устно решить задачи № 223 (а, б, г), 225, 226.

5. Перед введением классификации треугольников по углам (п. 31) учащимся задается вопрос: «Может ли треугольник иметь: а) два прямых угла; б) два тупых угла; в) один прямой и один тупой угол?».

Ответы должны быть обоснованы с помощью теоремы о сумме углов треугольника.

6. Записать в тетрадях вывод из этих ответов (следствие из теоремы о сумме углов треугольника): в любом треугольнике либо все три угла острые, либо два угла острые, а третий — тупой или прямой.

7. Ввести понятия остроугольного, тупоугольного и прямоугольного треугольников и обратить внимание учащихся на названия сторон прямоугольника, треугольника - гипотенуза и катет (рис. 126 учебника, модели треугольников).

 III. Закрепление изученного материала.

1. Решить задачи № 227(a) на доске и в тетрадях.

2. Решить задачу № 228 (а, в) на доске и в тетрадях.

Решение

1) Рассмотрим два случая:

а) угол при основании равен 40°, тогда второй угол при основании равнобедренного треугольника тоже равен 40°; значит, угол при вершине равен 180° - (40° + 40°) = 100°;

б) угол при вершине равен 40°, тогда углы при основании равны (180° - 40°) : 2 = 70°.

Ответ: 40°; 40° и 100° или 40°; 70°.

2) Опираемся на доказанное в задаче № 226 утверждение: углы при основании равнобедренного треугольника острые. Значит, угол при вершине равен 100°, а углы при основании равны (180° - 100°) : 2 = 40°.

Ответ: 100°; 40° и 40°.

IV. Итоги урока.

Домашнее задание: изучить пункты 30-31; ответить на вопросы 1; 3; 4; 5 на с. 89; решить задачи № 223 (б)-3, 228 (б)-4, 230-5.