Теорема Пифагора

? км

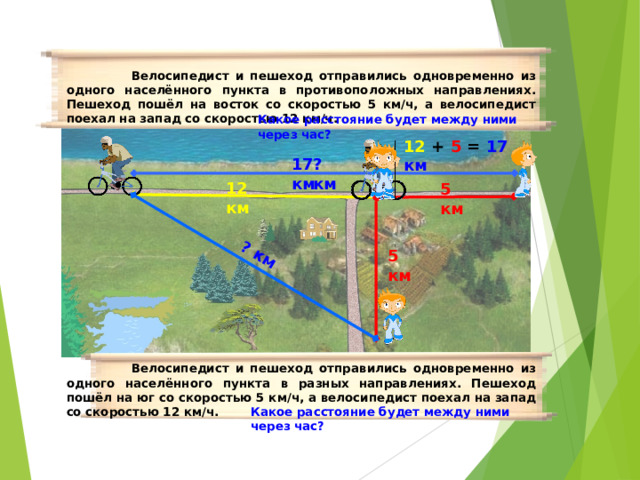
Велосипедист и пешеход отправились одновременно из одного населённого пункта в противоположных направлениях. Пешеход пошёл на восток со скоростью 5 км/ч, а велосипедист поехал на запад со скоростью 12 км/ч.

Какое расстояние будет между ними через час?

12 + 5 = 17 км

? км

17 км

12 км

5 км

5 км

Велосипедист и пешеход отправились одновременно из одного населённого пункта в разных направлениях. Пешеход пошёл на юг со скоростью 5 км/ч, а велосипедист поехал на запад со скоростью 12 км/ч.

Какое расстояние будет между ними через час?

«…Геометрия владеет двумя сокровищами – теоремой Пифагора и золотым сечением…» Иоганн Кеплер

Теорема Пифагора

4

Устная работа

А

1. Определите вид треугольника, изображённого на рисунке.

2. Назовите его стороны. Как они называются?

3. Как найти площадь этого треугольника?

В

С

Устная работа

4. Перечислите фигуры, изображенные на рисунке.

5. Как найти площадь квадрата ABCD?

6. Как найти площадь треугольника EKD?

7. Как найти площадь многоугольника?

А

В

E

K

С

D

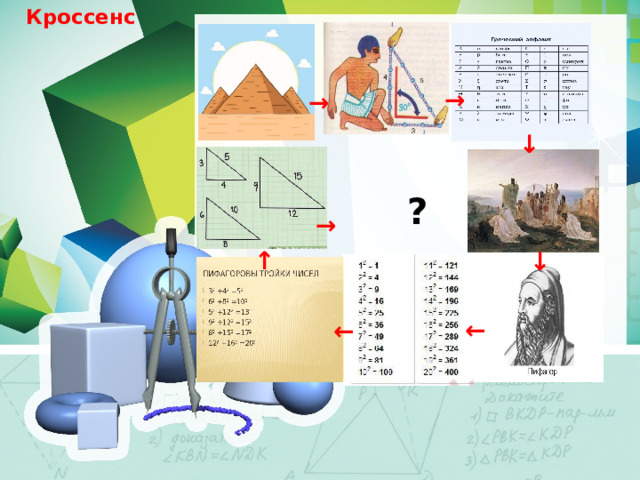
Кроссенс

→

→

↓

?

→

↑

↓

←

←

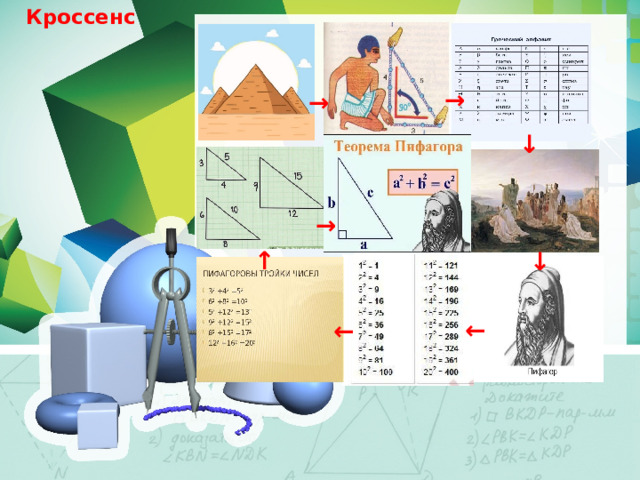
Кроссенс

→

→

↓

→

↑

↓

←

←

Практическая работа

План практической работы:

1. Измерьте катеты a, b и гипотенузу c. Результаты запишите в таблицу.

2. Найдите квадраты полученных величин a, b и c. Результаты запишите в таблицу.

3. Найдите сумму a² + b². Результат запишите в таблицу.

4. Сравните полученный результат с квадратом гипотенузы c².

5. Сделайте вывод.

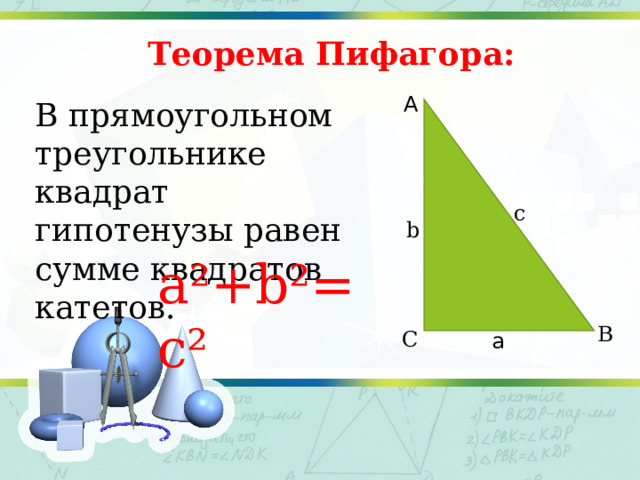
Теорема Пифагора:

А

В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

c

b

a²+b²=c²

В

С

a

Доказательство теоремы Пифагора

1. Достроим треугольник до квадрата со стороной a+b.

2. Его площадь равна S=(a+b)².

3. С другой стороны этот квадрат состоит из четырех равных треугольников:

Sтреуг=1/2ab;

4Sтреуг=2ab;

и квадрата со стороной с Sкв=с².

Отсюда S=2ab+c².

4. Следовательно

(a+b)²=2ab+c²;

a²+ b²+2ab=2ab+c²;

a²+b²=c².

Ч.т.д.

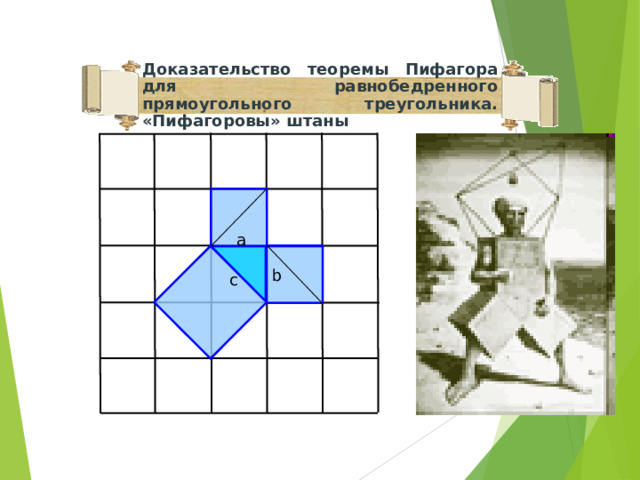
Доказательство теоремы Пифагора для равнобедренного прямоугольного треугольника. «Пифагоровы» штаны

a

b

c

? км

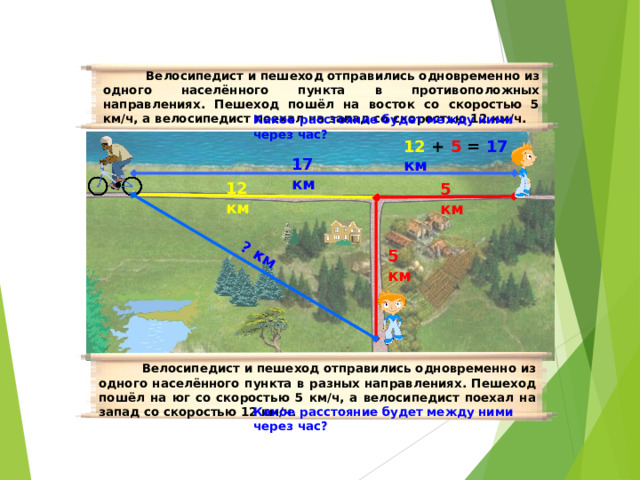
Велосипедист и пешеход отправились одновременно из одного населённого пункта в противоположных направлениях. Пешеход пошёл на восток со скоростью 5 км/ч, а велосипедист поехал на запад со скоростью 12 км/ч.

Какое расстояние будет между ними через час?

12 + 5 = 17 км

17 км

12 км

5 км

5 км

Велосипедист и пешеход отправились одновременно из одного населённого пункта в разных направлениях. Пешеход пошёл на юг со скоростью 5 км/ч, а велосипедист поехал на запад со скоростью 12 км/ч.

Какое расстояние будет между ними через час?

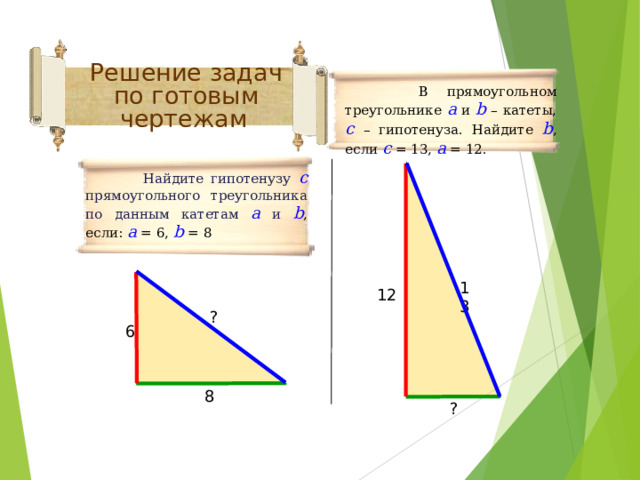
Решение задач по готовым чертежам

В прямоугольном треугольнике а и b – катеты, с – гипотенуза. Найдите b , если с = 13, а = 12.

Найдите гипотенузу с прямоугольного треугольника по данным катетам а и b , если: а = 6, b = 8

13

12

?

6

8

?

Астрономия

В 1974 году на созвездие Геркулес с Земли был отправлен сильный сигнал, который содержал в себе 1679 самых важных сообщений и открытий. Среди них была зашифрована и теорема Пифагора.

Самостоятельная работа

1. В прямоугольном треугольнике угол С=90 градусов. Катеты равны 15см и 20 см. Найдите гипотенузу.

2. В прямоугольнике АВСD диагональ АС=5дм, катет АВ=3дм. Найдите длину другого катета прямоугольника.

Контроль

1. 25 см

2. 4 дм

Вставка рисунка

Области применения теоремы Пифагора

литература

архитектура

астрономия

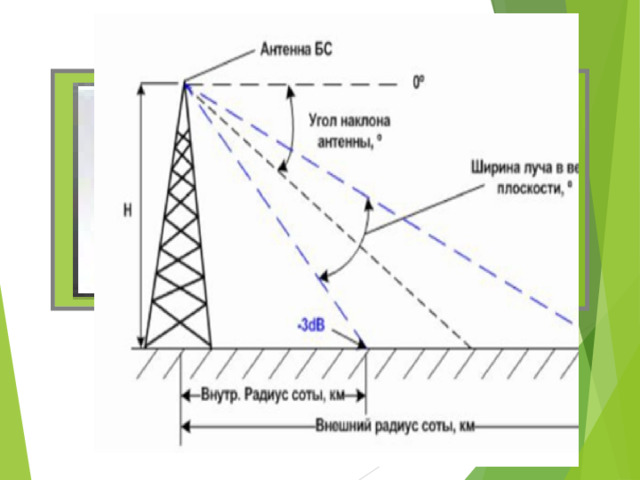
мобильная связь

вычисление длин отрезков

некоторых

фигур на плоскости

рефлексия

Суть истины вся в том, что нам она - навечно, Когда хоть раз в прозрении её увидим свет, И теорема Пифагора через столько лет Для нас. Как для него, бесспорна, безупречна…

А.Шамиссо