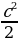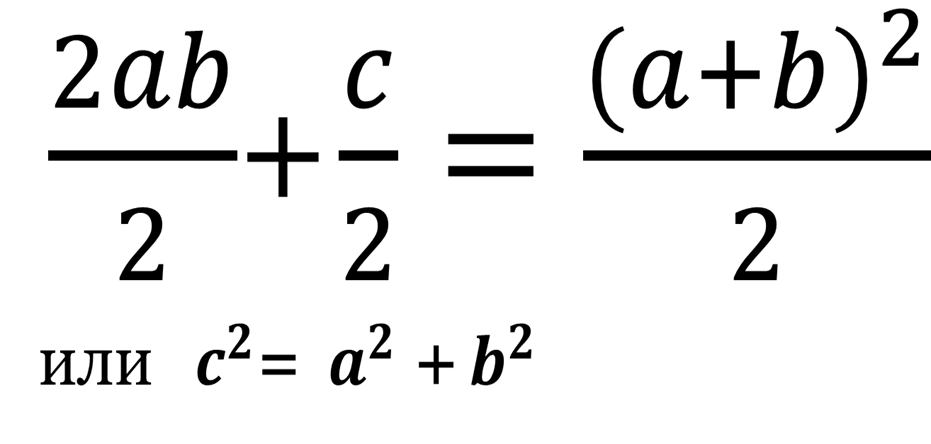Теорема Пифагора
Проект школьного научного общества «Поиск» обучающихся 8-х классов ЛОУ-СОШ №33
им. И.С. Малько
Слайд 2
Интересна история теоремы Пифагора
Хотя эта теорема и связана с именем Пифагора, она была известна задолго до него. В вавилонских текстах эта теорема встречается за 1200 лет до Пифагора, а в Египте это соотношение использовалось для построения прямого угла еще пять тысяч лет назад. Возможно, что тогда еще не знали ее доказательства, а само соотношение между гипотенузой и катетами было установлено опытным путем на основе измерений.
Слайд 3
Египетский треугольник
Египетский треугольник - это прямоугольный треугольник со сторонами 3, 4 и 5. Он получил такое название. оттого что был известен и широко применялся еще древними египтянами. Они с помощью такого треугольника строили прямые углы на местности, что имело для них огромное значение, так как каждый год разливы Нила размывали границы между полями, и приходилось заново размечать их
Слайд 4
Пифагор, по-видимому, нашел доказательство этого соотношения. Сохранилось древнее предание что в честь своего открытия Пифагор принес в жертву богам быка, по другим свидетельствам - даже сто быков. На протяжении последующих веков были найдены различные другие доказательства теоремы Пифагора. В настоящее время их насчитывается более пятиста, в том числе: геометрических, алгебраических, механических и прочих. Благодаря такому количеству доказательств, теорема Пифагора попала в Книгу рекордов Гиннеса, как теорема с наибольшим количеством доказательств.
Слайд 5
Известно множество вариантов доказательства этой теоремы. Над ними трудился и Евклид, и индийские ученые, и Леонардо да Винчи. Часто древние мудрецы приводили чертежи, примеры которых расположены выше, и не сопровождали их никакими объяснениями, кроме пометки «Смотри!»
Слайд 6
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
a2 + b2 = c2
Доказательство простейшее
Слайд 7.
Это доказательство получается в простейшем случае равнобедренного прямоугольного треугольника.
В самом деле, достаточно просто посмотреть на мозаику равнобедренных прямоугольных треугольников, чтобы убедиться в справедливости теоремы.
Например, для треугольника АВС: квадрат, построенный на гипотенузе АС, содержит 4 исходных треугольника, а квадраты, построенные на катетах, - по два. Теорема доказана.
Слайд8
Доказательство
Евклида
Слайд9
Доказательство Леонардо да Винчи
Слайд 10-12
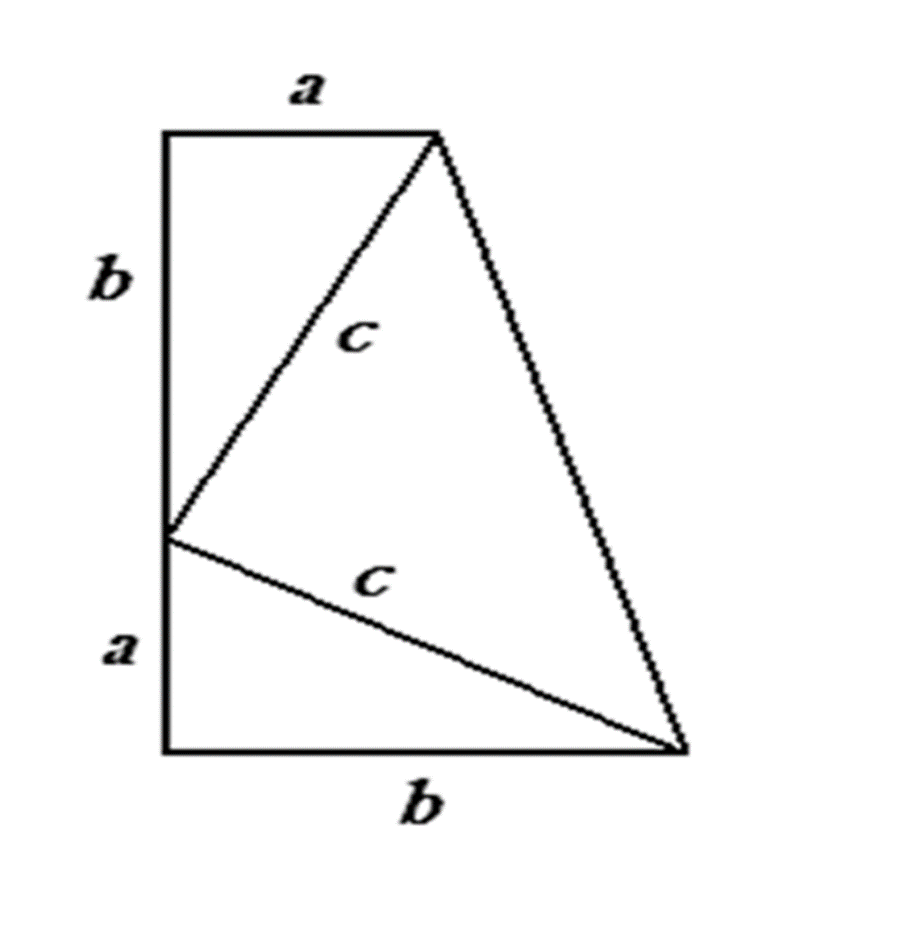
Доказательство
Дж. Гарлдфилда (1882 г.)
Расположим два равных прямоугольных треугольника так, чтобы катет одного из них был продолжением другого.
Площадь рассматриваемой трапеции находится как произведение полусуммы оснований на высоту.
Площадь трапеции
S=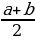 *(a+b)
*(a+b)
C другой стороны, площадь трапеции равна сумме площадей полученных треугольников:
S=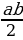 *2+
*2+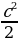
Приравнивая данные выражения, получаем:
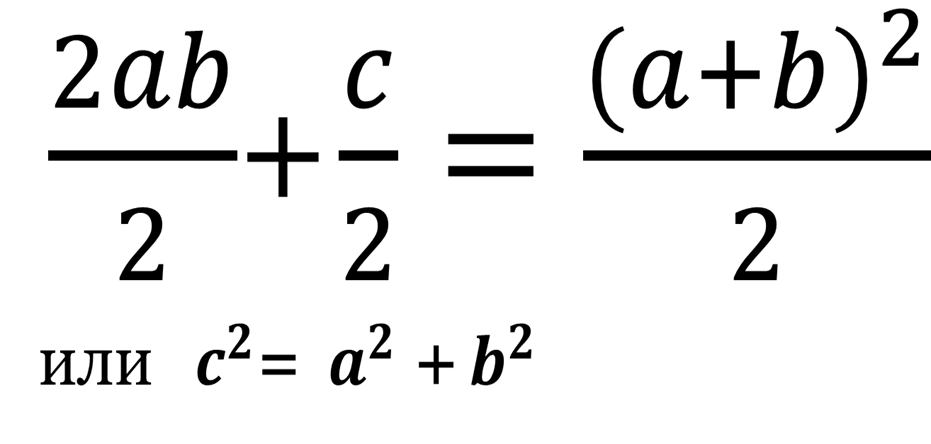
Слайд 13
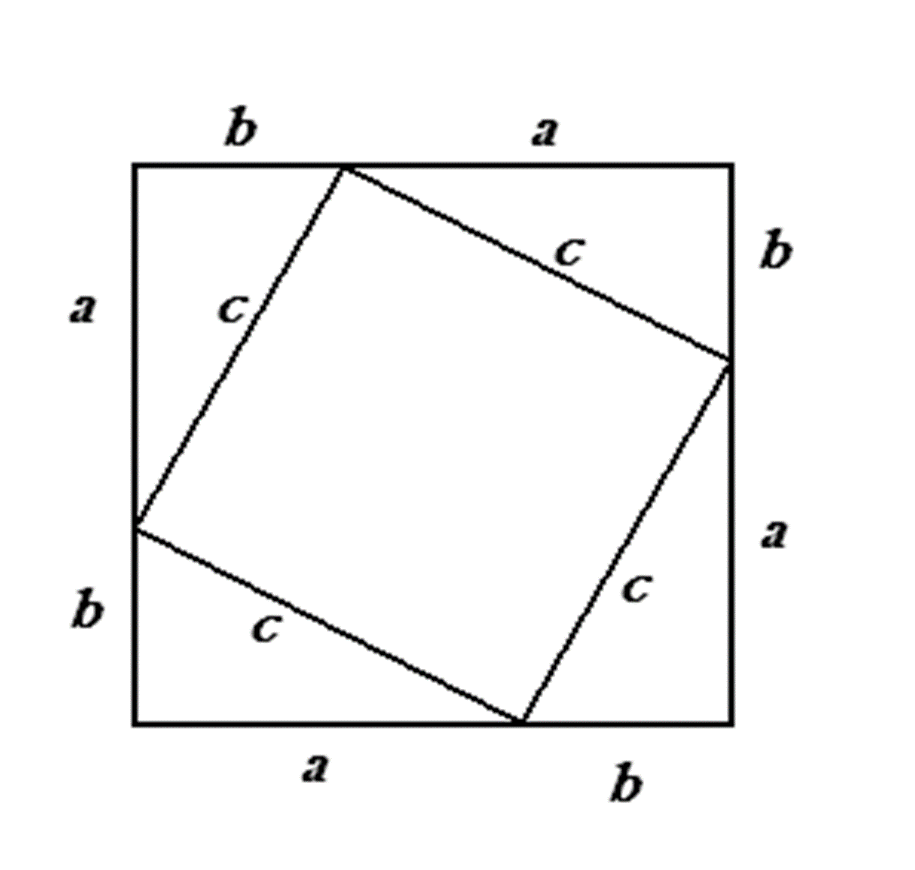
Древнекитайское доказательство
Такое доказательство дано и в нашем учебнике геометрии (автор Атанасян)
Слайд 17
Теорему в средние века называли «мостом ослов» , так как слабые ученики, заучивающие теоремы наизусть, без понимания, и прозванные поэтому «ослами», были не в состоянии преодолеть теорему Пифагора, служившую для них вроде непреодолимого моста.
Или «бегство убогих» , так как некоторые «убогие» ученики, не имевшие серьезной математической подготовки, бежали от геометрии.
Слайд 18
К теореме Пифагора его ученики составляли стишки, вроде:
«Пифагоровы штаны во все стороны равны».
Слайд 19
Она очень интересная и простая!!!








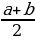 *(a+b)
*(a+b)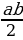 *2+
*2+