Теорема Пифагора

План урока №

Тема: Теорема Пифагора

Цель урока: Создать условия для совершенствования навыков решения задач на применение теоремы Пифагора и теоремы, обратной теореме Пифагора

Задачи:

научить применять теорему для решения задач;

показать связь между теоремой Пифагора и другими дисциплинами;

показать практическую значимость теоремы Пифагора;

развитие мировоззрения учащихся, алгоритмического, комплексного мышления.

Формируемые УУД

Личностные: учатся замечать и признавать свои ошибки, прислушиваться к мнениям одноклассников, анализировать, овладевать историческими и математическими знаниями и умениями, навыками их применения в реальной жизни, осознавать ценности исторических и математических знаний как важнейшего компонента научной картины мира, рефлексия.

Коммуникативные: планирование учебного сотрудничества с учителями и сверстниками, приобретают умения организовать сотрудничество с партнёром, осуществлять оценку действий партнера, умение с достаточной полнотой и точностью выражать свои мысли.

Регулятивные: осознание качества и уровня усвоения пройденного материала. Оценивают умение сотрудничать с учителем и одноклассниками.

Познавательные: устанавливают причинно-следственные связи между объектами, осуществляют подведение под понятие, проводят сравнение, классификацию объектов, выбирают наиболее эффективный способов решения задач.

Планируемые образовательные результаты

Метапредметные. Понимать связь математики с искусством, поэзией, философией, научиться чувствовать красоту формул и теорем, развивать интерес к истории математических открытий.

Личностные. Грамотно излагать свои мысли, анализировать, сравнивать, развивать познавательный интерес через творческие задания. Уметь самостоятельно приобретать новые знания и практические умения, управлять своей познавательной деятельностью. Развивать активность и находчивость при решении поставленных задач, умение работать в коллективе.

Предметные. Понимать, что такое «теорема Пифагора». Знать, как найти неизвестную сторону прямоугольного треугольника при помощи теоремы Пифагора. Уметь применять изученные понятия, методы для решения задач

Тип урока: Урок закрепления знаний и способов действий

Дидактические средства: учебник, задания для парной работы, тест.

Методы организации учебной деятельности: проблемный, частично-поисковый; исследовательский, наглядный, словесный.

Формы обучения: работа в парах (при взаимопроверке самостоятельной работы), фронтальная работа (в ходе решения задач и проведении математического диктанта), индивидуальная работа (в ходе закрепления изученного материала).

Приемы организации учебной деятельности: составление краткой записи к текстовым задачам, составление вопросов к текстовым задачам, самостоятельная работа, математический диктант.

Эпиграф урока

«…Геометрия владеет двумя сокровищами:

Одно из них - это теорема Пифагора,

которую можно сравнить с мерой золота»

Иоганн Кеплер.

Ход урока:

1. Мотивационно-организационный этап.

Добрый день! Располагайтесь поудобнее, начинаем наш урок.

Мы продолжаем изучение одной из самых известных теорем древности, теорему Пифагора. Значение теоремы Пифагора состоит и в том, что с ее помощью можно доказать многие другие теоремы и решить множество задач. Сегодня мы с вами рассмотрим некоторые практические задачи и старинные задачи, решаемые с помощью теоремы Пифагора.

2. Актуализация опорных знаний.

Еще в 17 веке немецкий астроном и математик И. Кеплер сказал, что геометрия обладает двумя великими сокровищами. Первое – это теорема Пифагора, которую можно сравнить с мерой золота…

Теорема Пифагора настолько известна, что трудно представить себе человека, не слышавшего о ней. Она одна из главных и, можно сказать, самая главная теорема геометрии. Значение ее состоит в том, что из нее или с ее помощью можно вывести большинство теорем геометрии. Заслуга же Пифагора состояла в том, что он дал полноценное научное доказательство этой теоремы.

Напомните, пожалуйста, формулировку теоремы Пифагора. (ответы учащихся)

А обратная теорема? (ответы учащихся)

Для того чтобы наша работа была успешной, давайте повторим некоторые геометрические факты

Математический диктант. ( 1 ученик работает за доской)

Закончи предложение:

– Сторона прямоугольного треугольника, прилежащая к прямому углу, называется…

– Один из углов прямоугольного треугольника, прилежащий к гипотенузе, равен 30. Чему равен второй угол, прилежащий к гипотенузе?...

– В треугольнике АВС угол А – прямой. Чем является в этом треугольнике отрезок ВС, катетом или гипотенузой?...

– Квадрат гипотенузы в прямоугольном треугольнике равен …

– В прямоугольном треугольнике катет, лежащий напротив угла в 30 равен…

Далее осуществляется проверка учащегося, работающего за доской и самопроверка ответов в своих тетрадях.

3. Решение практических задач в парах

Ребята, давайте внимательно прочитаем текст задачи, сделаем схематический чертеж и подумаем над ее решением.

1. Мальчик прошел от дома по направлению на восток 80м. Затем повернул на север и прошел 60м. На каком расстоянии (в метрах) от дома оказался мальчик?

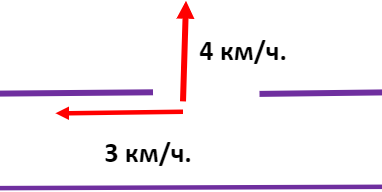
2. Мальчик и девочка, расставшись на перекрестке, пошли по взаимно перпендикулярным дорогам, мальчик со скоростью 4 км/ч, девочка — 3 км/ч. Какое расстояние (в километрах) будет между ними через 1 час?

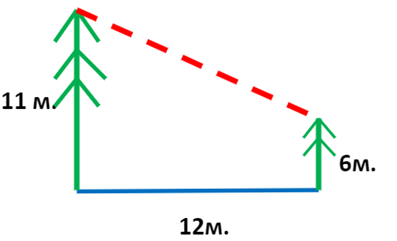
3. В 12 м одна от другой растут две сосны. Высота одной 11 м, а другой - 6 м. Найдите расстояние между их верхушками.

4. Решение старинных задач

1. Задача про сломленный тополь. (Фут – это старинная русская и английская мера длины = 30,5…см) Ответ: 6 футов, 244см.

2. Задача из учебника "Арифметика" Леонтия Магницкого (18 век)

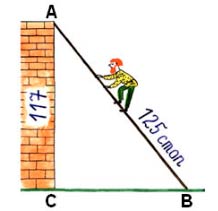
"Случися некому человеку к стене лестницу прибрати, стены же тоя высота есть 117 стоп. И обреете лестницу долготью 125 стоп. И ведати хочет, колико стоп сея лестницы нижний конец от стены отстояти имать." Ответ: 15625-13689=1936, 44 стопы

5. Итоги урока. Самостоятельная работа со взаимным контролем (5-7 минут).

Вспомним основные понятия. 1 вариант тест

2 вариант таблица

Выставление оценок.

- Я благодарю вас за работу. Поработали вы плодотворно, я оценю вашу работу так: …

6. Рефлексия. Заполняется таблица на карточках

- В завершении хотелось бы сказать: Причина популярности теоремы Пифагора триедина - это красота, простота и значимость!

7. ДЗ подготовка к контрольной работе и задача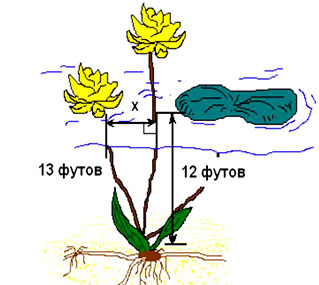

«У египтян была известна задача о лотосе. "На глубине 12 футов растет лотос с 13-футовым стеблем. Определите, на какое расстояние цветок может отклониться от вертикали, проходящей через точку крепления стебля ко дну”.

Приложение.

Тест по теме «Теорема Пифагора»

1. К каким треугольникам можно применить теорему Пифагора?

а) любым; б) прямоугольным; в) равносторонним

2. Верно ли, что в прямоугольном треугольнике любой из катетов меньше гипотенузы?

а) нет; б) не знаю; в) да

3. В прямоугольном треугольнике углы равны:

а) 90; 60; 90; б) 45; 90;45; в)60; 30; 60

4. В прямоугольном треугольнике одна из его сторон является проекцией другой стороны.

а) да; б) нет; в) не знаю.

5. Как называется прямоугольный треугольник с построенными на его катетах и гипотенузе квадратами?

а) треугольник Герона

б) Пифагорова фигура

в) многоугольник Фалеса

6. В прямоугольном треугольнике любой из катетов меньше гипотенузы.

а) да; б) нет; в) не знаю.

7. Какая из этих формул является формулой Пифагора?

а) d₁d₂ = ab + cd

б) S² = p(p - a)(p - b)(p - c)

в) а²+b²=с²

8. Определите катет, если другой катет равен 8 см, а гипотенуза – 10 см.

а) 12; б) 6; в) 4.