ТЕОРЕМА ПИФАГОРА
8 класс, 2 ч
Содержание
Теорема Пифагора.
Применение теоремы Пифагора к решению задач.
Цель изучения
Существенно расширить круг геометрических задач, решаемых школьниками.
Познакомить учащихся с основными этапами жизни и деятельности Пифагора.
Осуществление межпредметной связи геометрии с алгеброй, географией, историей, биологией, литературой.
Прогнозируемый результат
Знать зависимость между сторонами прямоугольного треугольника.
Уметь доказывать теорему Пифагора.
Уметь применять теорему Пифагора для решения задач.
План урока
Организационный момент.
Актуализация знаний.
Сообщение учащегося о жизни Пифагора Самосского.
Историческая справка о теореме Пифагора.
Работа над теоремой.
Решение задач с применением теоремы.
Подведение итога урока.
Домашнее задание.
Оборудование
Чертежные инструменты.
Портрет Пифагора.
Стенд с различными доказательствами теоремы Пифагора.
Рисунки к устным задачам.
Презентация Microsoft Office PowerPoint.
Ход урока
… Прежде, чем приступить к изучению нового материала, вспомним определение косинуса угла и решим несколько устных задач.
Дайте определение косинуса острого угла прямоугольного треугольника.
Чему равен cos A на рисунке 1?
Чему равен cos В на рисунке 2?
Чему равны косинусы острых углов Δ CDE на рисунке 3?
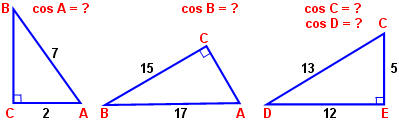
Рис. 1 – 3
О т в е т:
1) cos A = 2 / 7; 2) cos В = 15 / 17; 3) cos C = 5 / 13, cos D = 12 / 13
Сегодня на уроке мы приступает к изучению одной из важнейших теорем геометрии – теоремы Пифагора. Она является основой решения множества геометрических задач и базой изучения теоретического материала в дальнейшем. Докажем эту теорему и решим несколько задач с её применением, но сначала послушаем рассказ о математике, именем которого она названа.
Из рассказа вы узнали, что союз пифагорейцев был тайным. Эмблемой или опознавательным знаком союза являлась пентаграмма (рис. 4) – пятиконечная звезда. Пентаграмме присваивалась способность защищать человека от злых духов.

Рис. 4
У немецкого поэта Гёте в трагедии "Фауст", которую вы будете изучать на уроках литературы, описывается случай, когда дьявол Мефистофель проник в жилище учёного Фауста, потому что пентаграмма на его доме была плохо начерчена, и промежуток в уголке остался. Зачитаю вам эпизод.
| Мефистофель: | Нет, трудновато выйти мне теперь,
Тут кое-что мешает мне немного:
Волшебный знак у вашего порога. |
| Фауст: | Не пентаграмма ль этому виной?
Но как же, бес, пробрался ты за мной?
Каким путем впросак попался? |
| Мефистофель: | Изволили ее вы плохо начертить,
И промежуток в уголку остался,
Там, у дверей, и я свободно мог вскочить. |
Этот пятиугольник обладает интересным геометрическим свойством: поворотной симметрией пятого порядка, т.е. имеет пять осей симметрии, которые совмещаются при каждом повороте на 72º. Именно это тип симметрии наиболее распространён в живой природе у цветков незабудки, гвоздики, колокольчика, шиповника, лапчатки гусиной, вишни (рис. 5), груши, яблони, малины, рябины и т.д. Поворотная симметрия пятого порядка встречается и в животном мире, например, у морской звезды (рис. 6) и панциря морского ежа.



Рис. 5, 6
Пифагор сделал много важных открытий, но наибольшую славу учёному принесла доказанная им теорема, которая сейчас носит его имя.
Откройте тетради, запишите число … и тему урока "Теорема Пифагора".
— Ребята, может быть, вы что-нибудь слышали о теореме Пифагора? (…)
— А ещё? (Пифагоровы штаны во все стороны равны.)
Действительно, это шуточная формулировка теоремы.
В современных учебниках теорема сформулирована так: "В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов".
— Как записать теорему Пифагора для прямоугольного треугольника АВС с катетами а, b и гипотенузой с (рис. 7)?
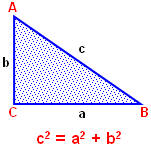
Рис. 7
Предполагают, что во времена Пифагора теорема звучала по-другому: "Площадь квадрата, построенного на гипотенузе прямоугольного треугольника, равна сумме площадей квадратов, построенных на его катетах". Действительно, с2 – площадь квадрата, построенного на гипотенузе, а2 и b2 – площади квадратов, построенных на катетах (рис. 8).
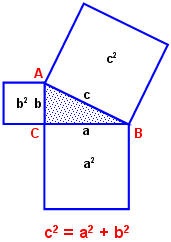
Рис. 8
Вероятно, факт, изложенный в теореме Пифагора, был сначала установлен для равнобедренных прямоугольных треугольников. Квадрат, построенный на гипотенузе, содержит четыре треугольника. А на каждом катете построен квадрат, содержащий два треугольника. Из рисунка 9 видно, что площадь квадрата, построенного на гипотенузе равна сумме площадей квадратов, построенных на катетах.
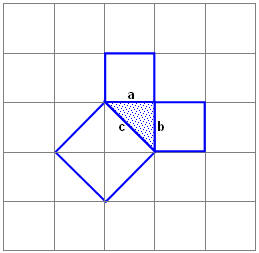
Рис. 9
Смотрите, а вот и "Пифагоровы штаны во все стороны равны" (рис.10):
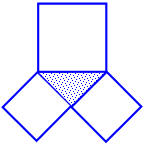
Рис. 10
Такие стишки придумывали учащиеся средних веков при изучении теоремы; рисовали шаржи. Вот, например, такие (рис. 11, рис. 12):
Рис. 11, 12
Интересна история теоремы Пифагора. Хотя эта теорема и связывается с именем Пифагора, она была известна задолго до него. В вавилонских текстах она встречается за 1200 лет до Пифагора. По-видимому, он первым нашёл её доказательство. Сохранилось древнее предание, что в честь своего открытия Пифагор принёс в жертву богам быка, по другим свидетельствам – даже сто быков. Это, однако, противоречит сведениям о моральных и религиозных воззрениях Пифагора. В литературных источниках можно прочитать, что он "запрещал даже убивать животных, а тем более ими кормиться, ибо животные имеют душу, как и мы". В связи с этим более правдоподобной можно считать следующую запись: "… когда он открыл, что в прямоугольном треугольнике гипотенуза имеет соответствие с катетами, он принес в жертву быка, сделанного из пшеничного теста".
На протяжении последующих веков были найдены другие доказательства теоремы Пифагора.
В настоящее время их насчитывается более ста.
Большинство способов её доказательства сводятся к разбиению квадратов на более мелкие части. На стенде вы можете познакомиться с двадцатью тремя такими доказательствами.
А сейчас докажем теорему Пифагора в современной формулировке.
Т е о р е м а. В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
Начертите треугольник АВС с прямым углом С (рис. 13).
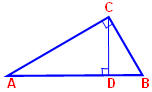
Рис. 13
Д а н о: Δ АВС, ∠ С = 90°.
Д о к а з а т ь: АВ2 = АС2 + ВС2.
Д о к а з а т е л ь с т в о
1.Проведём высоту CD из вершины прямого угла С.
Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе, поэтому
в Δ ACD cos A = AD / AC,
в Δ АВС cos А = AC / AB.
2.Так как равны левые части этих равенств, то равны и правые, следовательно, AD / AC = AC / AB.
Отсюда, по свойству пропорции, получаем: АС2 = AD · АВ.(1)
3.Аналогично,
в Δ ВCD cos В = BD / BC,
в Δ АВС cos В = BC / AB.
4.Так как равны левые части этих равенств, то равны и правые, следовательно, BD / BC = BC / AB.
5.Отсюда, по свойству пропорции, получаем: ВС2 = ВD · АВ.(2)
6.Сложим почленно равенства (1) и (2), и вынесем общий множитель за скобки:
АС2 + ВС2 = AD · AB + BD · AB = AB · (AD + BD).
Так как AD + BD = АВ, то АС2 + ВС2 = AB · AB = AB2.
Получили, что АВ2 = АС2 + ВС2.
Итак,
| Если дан нам треугольник
И притом с прямым углом,
То квадрат гипотенузы
Мы всегда легко найдём:
Катеты в квадрат возводим,
Сумму степеней находим
И таким простым путём
К результату мы придём. |
Ч. т. д.





























