Теория графов 5 класс

Умение решать задачи - такое же практическое искусство, как умение плавать или бегать.

Ему нужно научиться только путем подражания или упражнения.

Д. Пойа

Теория графов

учитель математики

МБОУ СОШ №11 г.Обнинска

Куракина Светлана Михайловна

Графы – математические объекты, с помощью которых можно решать много различных, внешне не похожих друг на друга задач.

В математике существует целый раздел – теория графов, который изучает графы, их свойства и применение.

Первая работа по теории графов

принадлежит Леонарду Эйлеру(1736год)

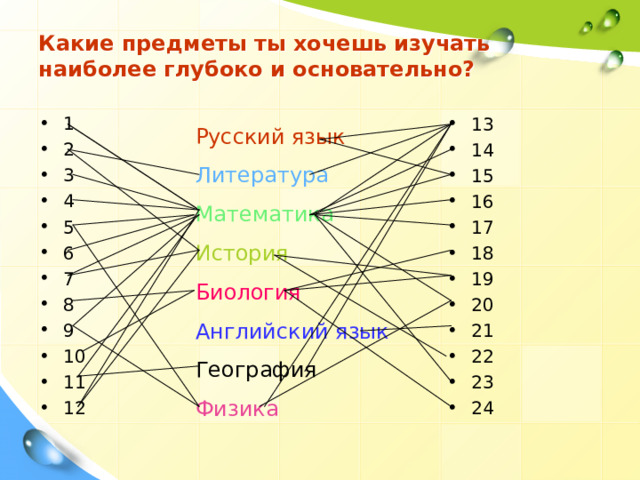
Какие предметы ты хочешь изучать наиболее глубоко и основательно?

• 13
• 14
• 15
• 16
• 17
• 18
• 19
• 20
• 21
• 22
• 23
• 24

• 1
• 2
• 3
• 4
• 5
• 6
• 7
• 8
• 9
• 10
• 11
• 12

Русский язык

Литература

Математика

История

Биология

Английский язык

География

Физика

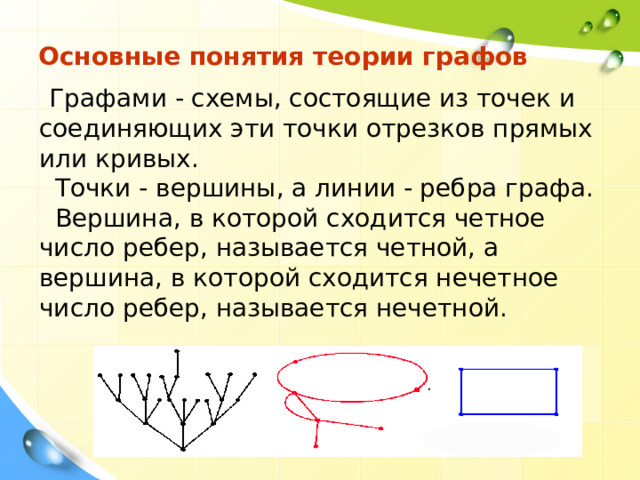
Основные понятия теории графов

Графами - схемы, состоящие из точек и соединяющих эти точки отрезков прямых или кривых.

Точки - вершины, а линии - ребра графа.

Вершина, в которой сходится четное число ребер, называется четной, а вершина, в которой сходится нечетное число ребер, называется нечетной.

.

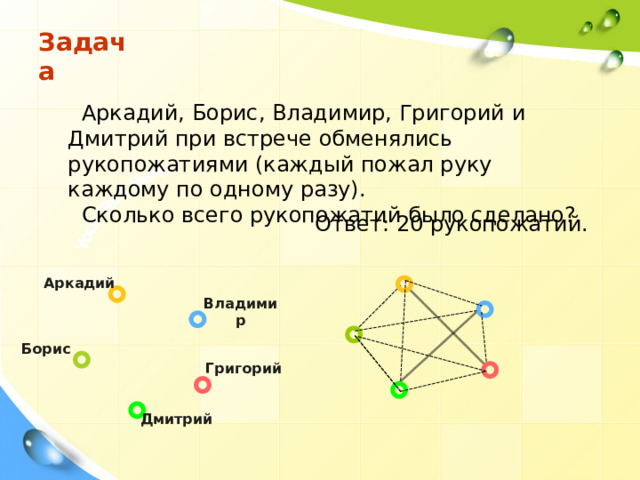
Задача

Аркадий, Борис, Владимир, Григорий и Дмитрий при встрече обменялись рукопожатиями (каждый пожал руку каждому по одному разу).

Сколько всего рукопожатий было сделано?

Ответ: 20 рукопожатий.

Аркадий

Владимир

Борис

Григорий

Дмитрий

Задача

Можно ли нарисовать изображенный на рисунке граф не отрывая карандаш от бумаги и проводя каждое ребро ровно один раз ?

Решение: если мы будем рисовать граф так, как сказано в условии, то в каждую вершину, кроме начальной и конечной, мы войдем столько же раз, сколько выйдем из нее. То есть все вершины графа, кроме двух должны быть четными. В нашем же графе имеется три нечетные вершины, поэтому его нельзя нарисовать указанным в условии способом.

Сейчас мы доказали теорему об Эйлеровых графах:

Теорема: Эйлеров граф должен иметь не более двух нечетных вершин.

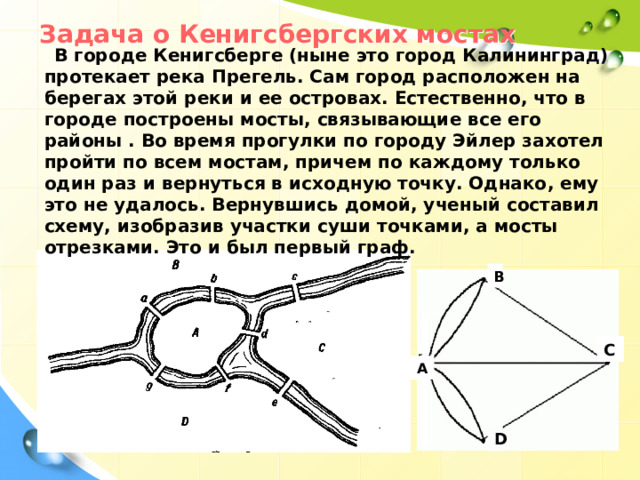
Задача о Кенигсбергских мостах

В городе Кенигсберге (ныне это город Калининград) протекает река Прегель. Сам город расположен на берегах этой реки и ее островах. Естественно, что в городе построены мосты, связывающие все его районы . Во время прогулки по городу Эйлер захотел пройти по всем мостам, причем по каждому только один раз и вернуться в исходную точку. Однако , ему это не удалось. Вернувшись домой, ученый составил схему, изобразив участки суши точками, а мосты отрезками. Это и был первый граф.

В

С

А

D

Задача космонавта №1:

Между девятью планетами солнечной системы установлено космическое сообщение. Рейсовые ракеты летают по следующим маршрутам: Земля – Меркурий; Плутон – Венера; Земля – Плутон; Плутон – Меркурий; Меркурий – Венера, Уран – Нептун; Нептун – Сатурн; Сатурн – Юпитер; Юпитер – Марс и Марс – Уран.

Можно ли долететь на рейсовых ракетах с Земли до Марса ?

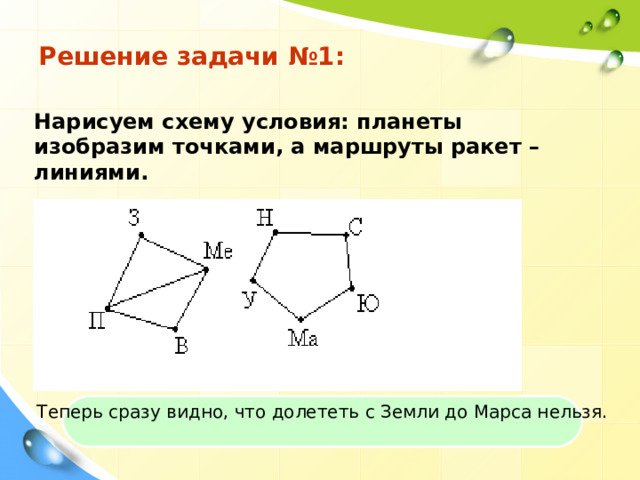
Решение задачи №1:

Нарисуем схему условия: планеты изобразим точками, а маршруты ракет – линиями.

Теперь сразу видно, что долететь с Земли до Марса нельзя.

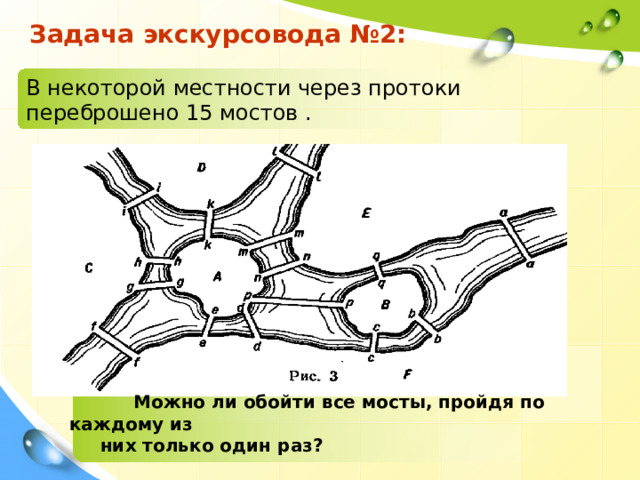
Задача экскурсовода №2:

В некоторой местности через протоки

переброшено 15 мостов .

Можно ли обойти все мосты, пройдя по каждому из

них только один раз?

Задача телефониста №3:

В городе Маленьком 15 телефонов. Можно ли их соединить проводами так, чтобы каждый телефон был соединен ровно с пятью другими ?

Решение задачи №3:

Представим себе граф, в котором вершины обозначают телефоны, а ребра – провода, их соединяющие 15*5:2=37,5 (т.к. каждый провод имеет два конца, то при суммировании степеней каждый провод будет взят 2 раза).

Title in here

Ответ: Соединить телефоны таким образом невозможно.

Задача модельера №4:

У Даши 4 блузки – красная, желтая, голубая, зеленая и 3 юбки – синяя, черная и оранжевая. Сколько у Даши вариантов подбора костюма?

Content Layouts

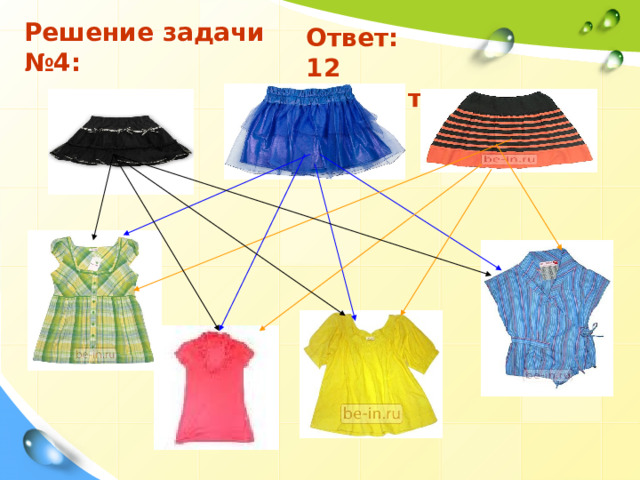
Решение задачи №4:

Ответ:

12 вариантов.

Задача о строительстве дорог №5: О трех домах и трех колодцах.

Имеется три дома и три колодца, каким-то образом расположенные на местности. Провести от каждого дома к каждому колодцу дорогу так, чтобы дороги не пересекались.

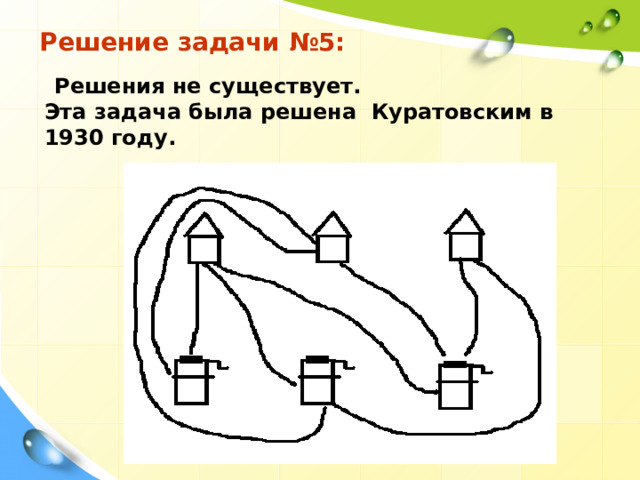
Решение задачи №5:

Решения не существует.

Эта задача была решена Куратовским в 1930 году.

Задача администратора магазина №6:

Администратор магазина формирует подарки к 8 марта. Для этого он закупил 2 книги, 4 блокнота и 3 ручки. Администратор хочет скомплектовать из этих предметов подарок, состоящий из 1 книги, 1 блокнота и 1 ручки. Сколько есть вариантов выбора?

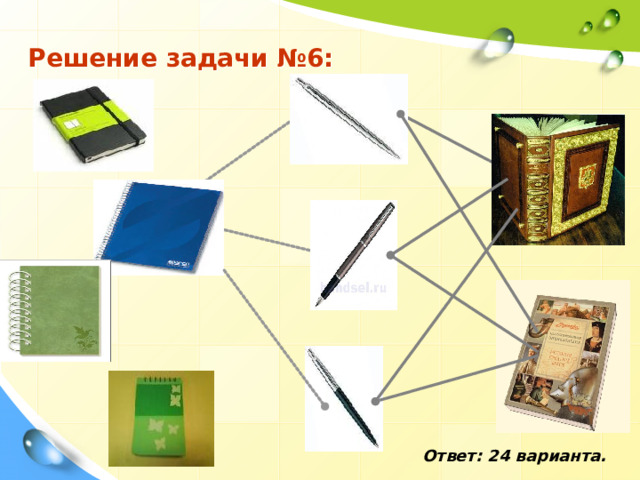
Решение задачи №6:

Ответ: 24 варианта.

Домашнее задание:

Нарисовать в тетради несколько вариантов своего пути от дома до школы

и выбрать из них кратчайший, выделив его особым цветом (с учетом

правил дорожного движения).

Выводы:

• Многие логические задачи лучше представить в виде чертежа, рисунка, схемы, в которых используются графы. Это облегчает решение задачи, делает его более убедительным и наглядным.
• Знание теории графов дают возможность приобрести навыки решения реальных ситуаций, научиться строить простейшие алгоритмы.

Your text in here

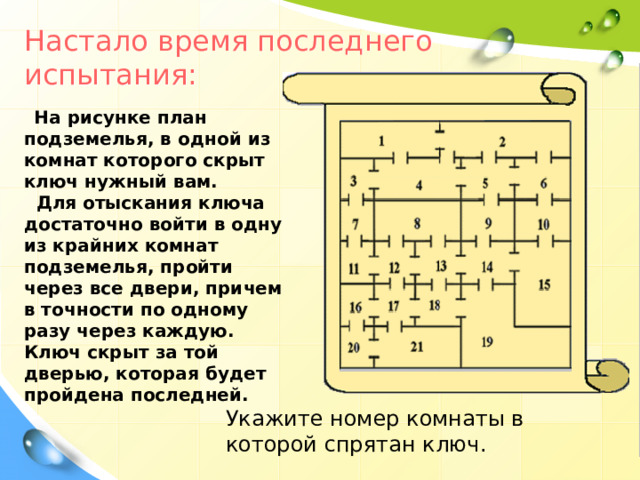
Настало время последнего испытания :

На рисунке план подземелья, в одной из комнат которого скрыт ключ нужный вам.

Для отыскания ключа достаточно войти в одну из крайних комнат подземелья, пройти через все двери, причем в точности по одному разу через каждую. Ключ скрыт за той дверью, которая будет пройдена последней.

Укажите номер комнаты в которой спрятан ключ .