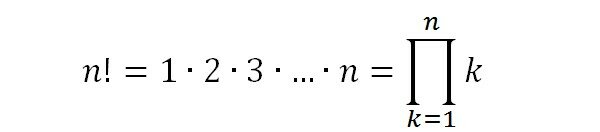Муниципальное общеобразовательное учреждение
«Средняя общеобразовательная школа № 10
с. Солдато-Александровского Советского района»
Ставропольского края
Разработка урока на тему
«Вероятность и статистика»
Подготовила учитель математики
Плотникова О.Г.
2022-2023 учебный год
Я говорю вам: «Здравствуйте», желая этим словом
Здоровья,
Добрых дел побольше,
Работоспособности,
Аккуратности,
Внимательности на уроке,
Стремления,
Творчества,
Воодушевления,
Умения слушать и слышать,
Интересных задач,
Терпения в работе,
Единства при работе в паре!
Ведь именно так мы планируем работать на сегодняшнем уроке
Внимание на экран. Ваши ассоциации?
/на слайде поочерёдно появляются предметы: шахматы, шарф, кепка, стул
В город молодой человек вошел к, зеленом в талию костюме. Его могучая шея была несколько раз обернута старым шерстяным шарфом, ноги были в лаковых штиблетах с замшевым верхом апельсинного цвета. Носков под штиблетами не было.
/отрывок из кинофильма «12 СТУЛЬЕВ» о великом комбинаторе
Ребята, давайте определим тему нашего урока (Теория вероятностей, комбинаторика и статистика)
Девиз сегодняшнего урока - высказывание писателя Брайна Герберта: «Оптимизм, вероятно, лучшее оружие, каким располагает человечество. Без него мы бы никогда не решились совершать невозможное, которое — вопреки всем вероятностям — оказывается возможным»
Работа с кейсом
Очень часто приходится решать задачи, в которых надо посчитать количество возможных вариантов для той или иной ситуации. Например, сколько позиций может возникнуть на шахматной доске после первого хода обоих игроков? Сколько разных паролей длиною в десять символов можно записать, если ни один символ не использовать дважды? Сколько разнообразных комбинаций чисел может выпасть при игре в лотерею «6 из 49»? На все эти вопросы помогает ответить специальный раздел математики, называемый комбинаторикой. Почти всегда комбинаторную задачу можно сфорулировать так, чтобы ее вопрос начинался словами «сколькими способами…». Комбинаторика – раздел математики, который изучает задачи выбора и расположения элементов из некоторого основного множества в соответствии с заданными правилами. Формулы и принципы комбинаторики используются в теории вероятностей для подсчета вероятности случайных событий и, соответственно, получения законов распределения случайных величин. Это, в свою очередь, позволяет исследовать закономерности массовых случайных явлений, что является весьма важным для правильного понимания статистических закономерностей, проявляющихся в природе и технике.
Правила сложения и умножения в комбинаторике
Правило суммы. Если два действия А и В взаимно исключают друг друга, причем действие А можно выполнить m способами, а В – n способами, то выполнить одно любое из этих действий (либо А, либо В) можно n + m способами.
Пример 1.
В классе учится 16 мальчиков и 10 девочек. Сколькими способами можно назначить одного дежурного?
Решение
Дежурным можно назначить либо мальчика, либо девочку, т.е. дежурным может быть любой из 16 мальчиков, либо любая из 10 девочек.
По правилу суммы получаем, что одного дежурного можно назначить 16+10=26 способами.
Правило произведения. Пусть требуется выполнить последовательно k действий. Если первое действие можно выполнить n1 способами, второе действие n2 способами, третье – n3 способами и так до k-го действия, которое можно выполнить nk способами, то все k действий вместе могут быть выполнены:
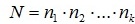
Пример 2.
В классе учится 16 мальчиков и 10 девочек. Сколькими способами можно назначить двух дежурных?
Решение
Первым дежурным можно назначить либо мальчика, либо девочку. Т.к. в классе учится 16 мальчиков и 10 девочек, то назначить первого дежурного можно 16+10=26 способами.
После того, как мы выбрали первого дежурного, второго мы можем выбрать из оставшихся 25 человек, т.е. 25-ю способами.
По теореме умножения двое дежурных могут быть выбраны 26*25=650 способами
Факториал - это математическая функция, применяемая к неотрицательным целым числам, равная произведению всех натуральных чисел от 1 до числа, для которого она вычисляется. Обозначается она очень просто: n! (произносится "эн факториал") - да, просто приписывается восклицательный знак к числу :) Чтобы было легче понять определение факториала, сразу пример: 5!=1х2х3х4х5=120. То есть, чтобы найти факториал числа, нужно просто поочереди перемножить все натуральные числа от единицы до самого числа включительно. Математически определение факториала выглядит так:
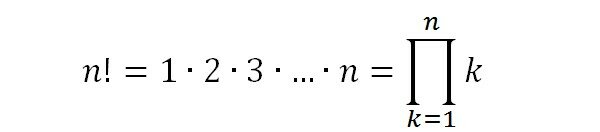
Факториал очень активно используется в различных разделах математики, особенно там, где заходит речь о различных вариантах, перестановках, комбинациях и т. п. Он применяется в комбинаторике, теории чисел, математическом анализе и других областях. Очень хорошо становится понятным смысл факториала при изучении и применении вышеозвученной комбинаторики. В ней факториал натурального числа n интерпретируется как количество перестановок множества из n элементов. Что это означает на практике? Разберём задачу.
В гостиной стоит стол с четырьмя стульями вокруг. В комнату заходит четыре человека. Сколько существует вариантов для рассаживания вокруг стола всех четырёх человек?
Как раз для решения подобных задач требуется факториал. Зная его определение, задача решается в одно действие: 4!=1х2х3х4=24. То есть, ответ: 24 варианта (комбинации).
По окончании работы с текстом заполните блок-схемы:
Почти всегда комбинаторную задачу можно сфорулировать так, ________________________________________________ чтобы _________________________________________________. Комбинаторика – раздел математики, который изучает _________________________________________________________________________________________________________________________________________________________________________________________. Формулы и принципы комбинаторики используются ____________________________________________________________________________________________________________________________________________________________________________________________. Это, в свою очередь, позволяет исследовать закономерности массовых случайных явлений, что является весьма важным для правильного понимания статистических закономерностей, проявляющихся в природе и технике.
Правило суммы. Если два действия А и В взаимно исключают друг друга, причем действие А можно выполнить m способами, а В – n способами, _______________________________________________________________________________________________________________________ способами.
Правило произведения. Пусть требуется выполнить последовательно k действий. Если первое действие можно выполнить n1 способами, второе действие n2 способами, третье – n3 способами и так до k-го действия, которое можно выполнить nk способами, то все k действ
Предлагаю поработать с сайтом «Решу ОГЭ»
1. Если на тарелке лежат 5 груш и 4 яблока, то выбрать один фрукт (грушу или яблоко) можно 9 способами (5 + 4 = 9). В общем виде справедливо такое утверждение:
2. Несколько стран решили использовать для своего государственного флага символику в виде трех горизонтальных полос одинаковой ширины разных цветов – белого, синего, красного. Сколько стран могут использовать такую символику при условии, что у каждой страны – свой флаг?
КБС – Люксембург и Нидерланды.
СКБ- Франция
Решение:Р3= 3! = 6.
Предлагаю небольшую викторину про Российский флаг:
Вспомните, что означает каждый цвет нашего флага. (Белый - благородство, долг, цвет чистоты. Синий - верность и целомудрие, цвет любви. Красный - мужество и великодушие, цвет силы.)
Какой цвет считался императорским (царским) и какой цвет считался символом вечности? (Красный, золотой).
Сколько флагов было в период царствования Петра I? (Три).
Кто ввёл порядок расположения цветов? (Пётр I.)
Какое старинное русское название флага? (Стяг)
20 января 1705 году бело-сине-красный флаг стал официально указы-вать на государственную принадлежность. С чем связана эта дата? (в этот день Петр Первый передал бело-синий-красный флаг торговому флоту. Российский флаг стал приниматься во всех странах как государственный флаг России).
С 1918 года до августа 1991 года флагом России был красный стяг, какое название он носит сейчас? (Знамя Победы)
3. Составьте всевозможные трёхзначные числа, в которых все цифры разные, используя лишь цифры:
а) 7, 5, 1; б) 2, 0, 9.
Решение:
а) Р3= 3! = 6 – всего 6 чисел: 751, 715, 571, 517, 175, 157.
4. Учащиеся должны посетить во вторник по расписанию 5 уроков по следующим предметам: литература, алгебра, география, физкультура и биология. Сколькими способами можно составить расписание на этот день, чтобы физкультура была пятым уроком?
Решение: Р4 = 4! = 24.
Ответ: 24 способа.
Может ли комбинаторика помочь в реальной жизни? (обсуждение) Выдвижение гипотезы:
Комбинаторика интересна и имеет широкий спектр практической направленности.
/Работа в парах:
Установить соответствие между науками, сферами нашей жизни и задачами, которые решает комбинаторика.
| учебные заведения |
|
| сфера общественного питания |
|
| лингвистика |
|
| география |
|
| биология |
|
| химия |
|
| экономика |
|
| игры |
|
/Примерные ответы детей:
-учебные заведения (составление расписаний)
-сфера общественного питания (составление меню)
-лингвистика (рассмотрение вариантов комбинаций букв)
-география (раскраска карт)
-биология (расшифровка кода ДНК)
-химия (анализ возможных связей между химическими элементами)
-экономика (анализ вариантов купли-продажи акций)
-игры (подсчѐт частоты выигрышей)