Тест по алгебре 10 класс по теме "Применение производной"

Тест по теме «Применение производной» 10 кл

1. Критическими точками первого рода функции 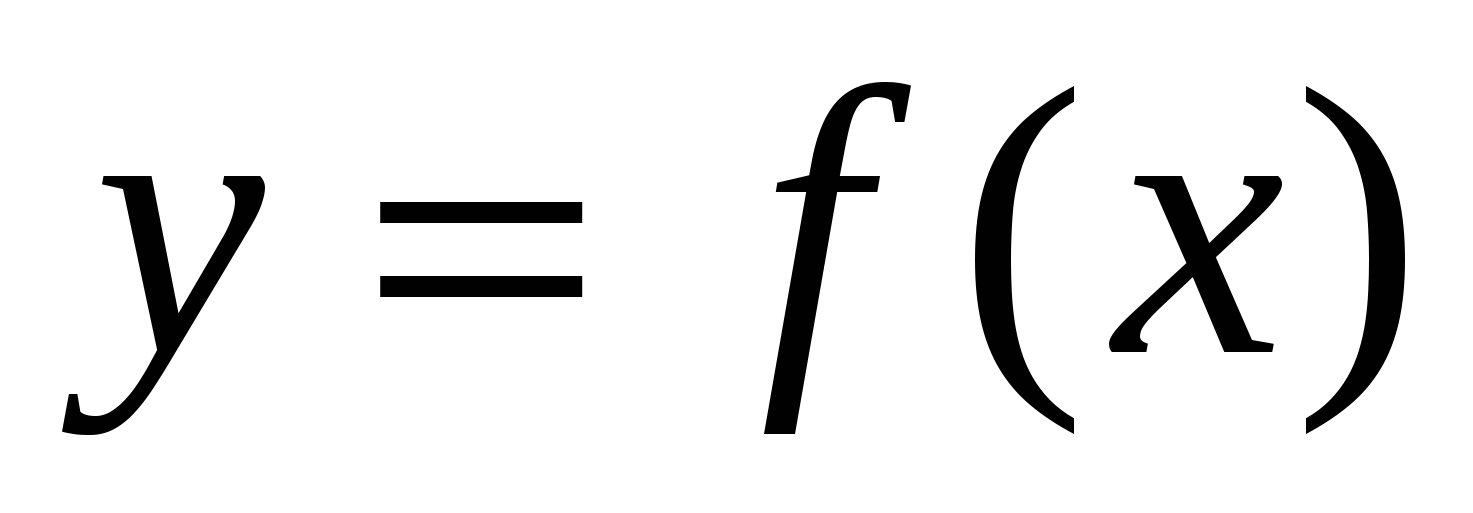  называются те значения аргумента, в которых:

а) функция обращается в нуль;

б) функция равна  ;

в ) производная равна нулю

г) производная не существует;

д) производная отрицательна;

2. Указать промежутки возрастания функции 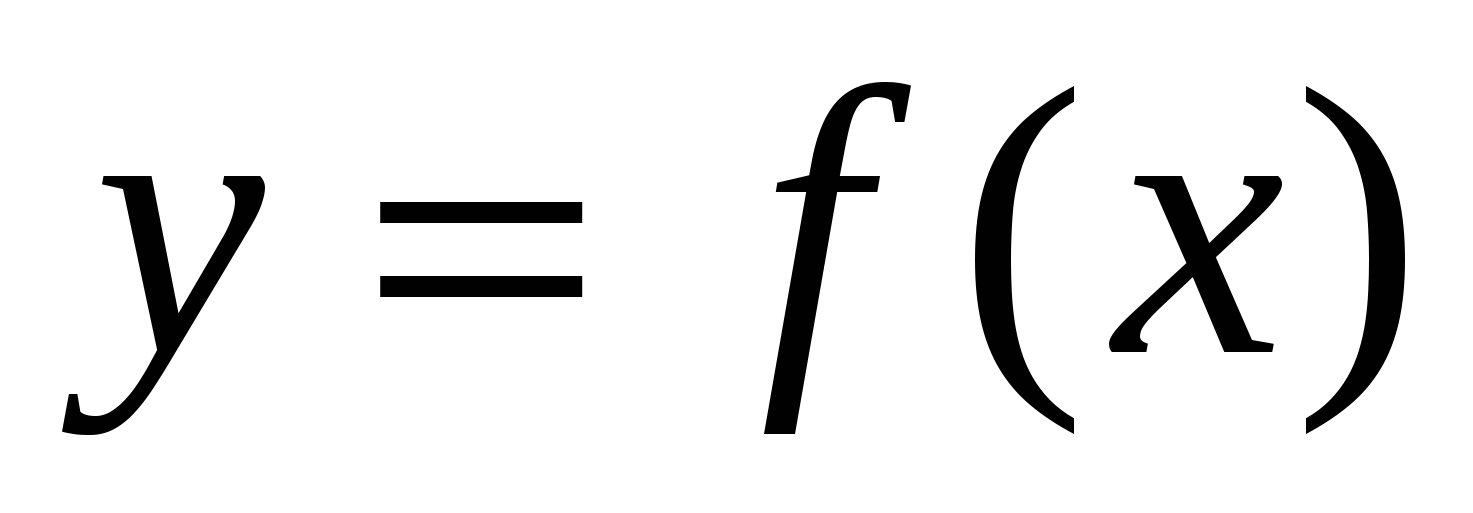 , изображенной на графике

а) (-5;6);

б) (6;13);

в)  ;

г) 

3. Кривая 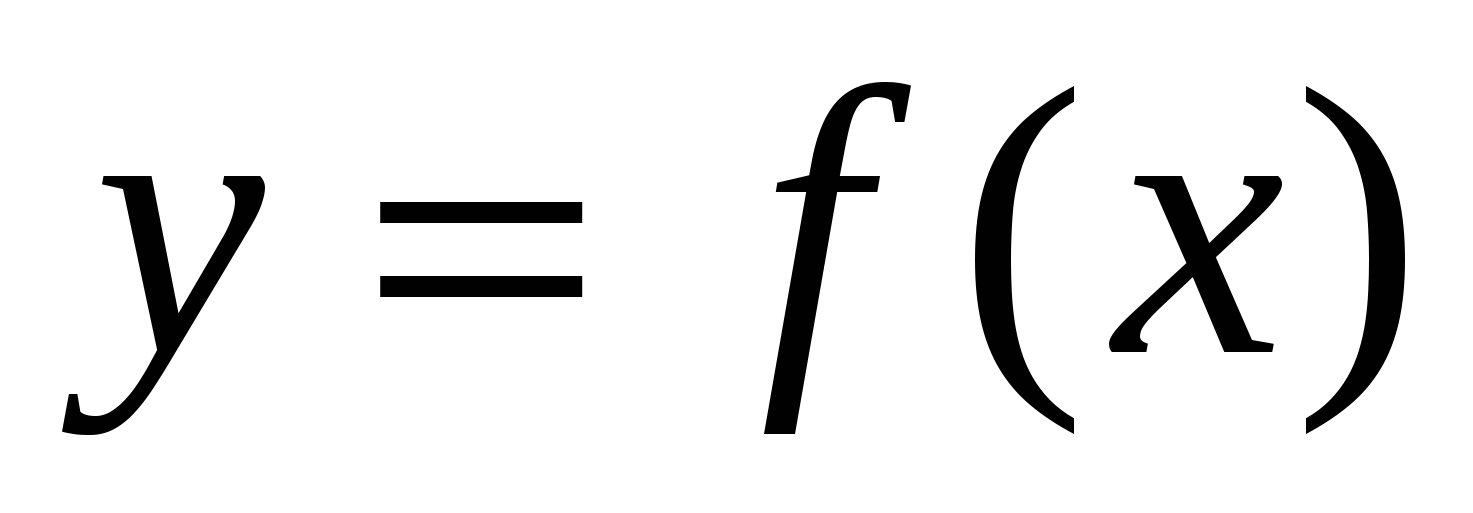  является выпуклой на интервале (a;b), если на заданном интервале выполняется условие:

а)  ;

б)  ;

в)  ;

г)  ;

д)  .

4. Если x₀ - критическая точка и при переходе через неё слева направо первая производная меняет знак с «+» на «-», то в данной точке:

а) минимум

б) максимум

в) перегиб функции

г) функция обращается в ноль

5. Указать точки экстремума функции  :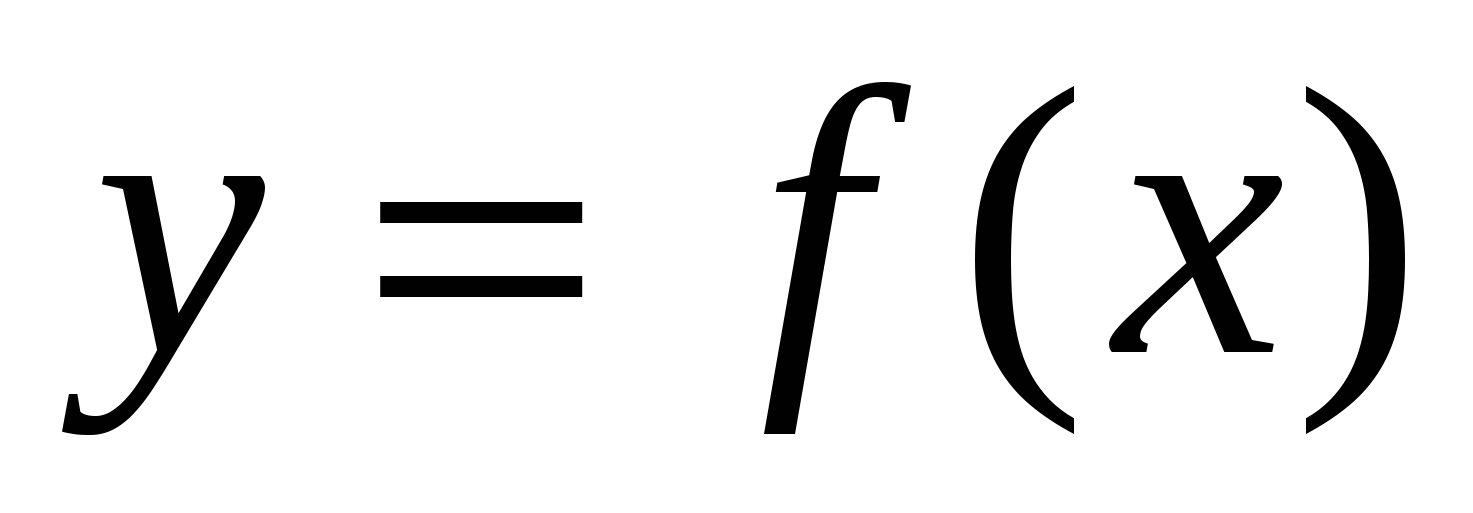

а) max(-2;4); min(9;6); max(3;-2);

б) min(-2;4); min(9;6); max(3;-2);

в) max(-2;4); max(9;6); min(3;-2);

г) max(3;-2); min(9;6); max(-2;4).

6. Если для функции  на интервале (a;b) выполняется условие  , то…

а) на данном интервале она выпукла

б) на данном интервале она вогнута

в) на данном интервале она убывает

г) на данном интервале она возрастает

д) функция обращается в ноль

7. Если X₀ - критическая точка и при переходе через неё слева направо производная меняет знак с "-" на "+", то в данной точке:

а) минимум

б) максимум

в) перегиб функции

8. Точка а является точкой перегиба данной кривой 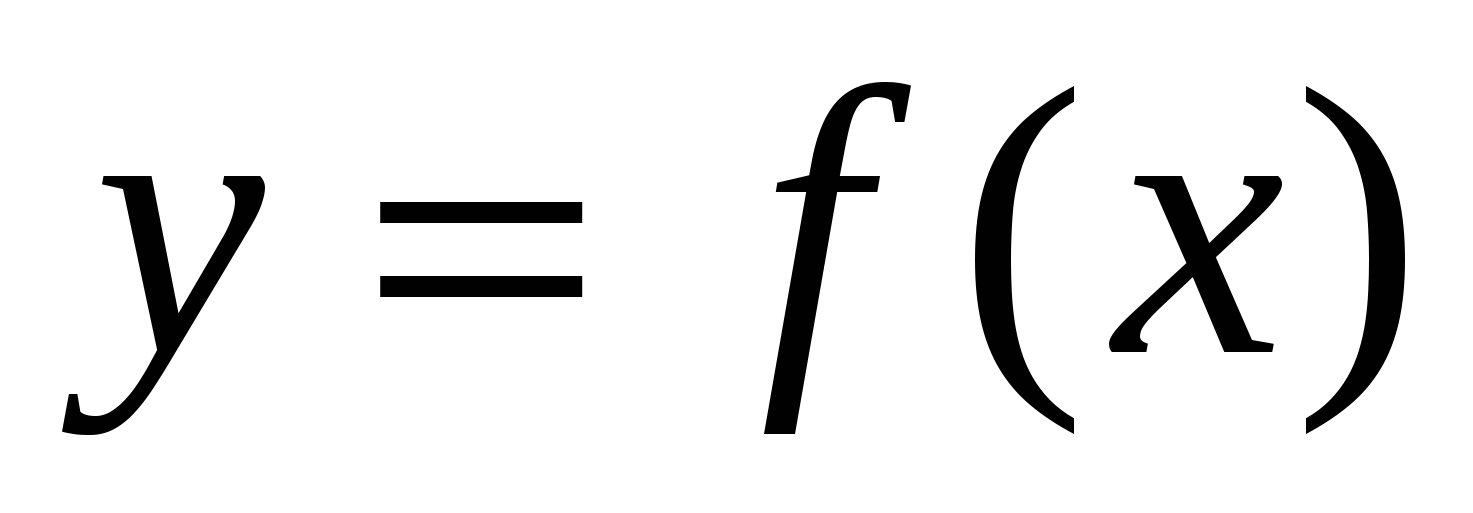 , если:

а)  ;

б)  ;

в)  ;

г)  ;

д) 

9. Укажите порядок нахождения экстремумов функции

1. разбить числовую прямую критическими точками на промежутки

2. найти знак первой производной в каждом числовом промежутке

3. найти первую производную функции

4. установить по знаку первой производной точки min и max

5. приравнять первую производную к нулю и найти критические точки

10. Указать промежутки убывания функции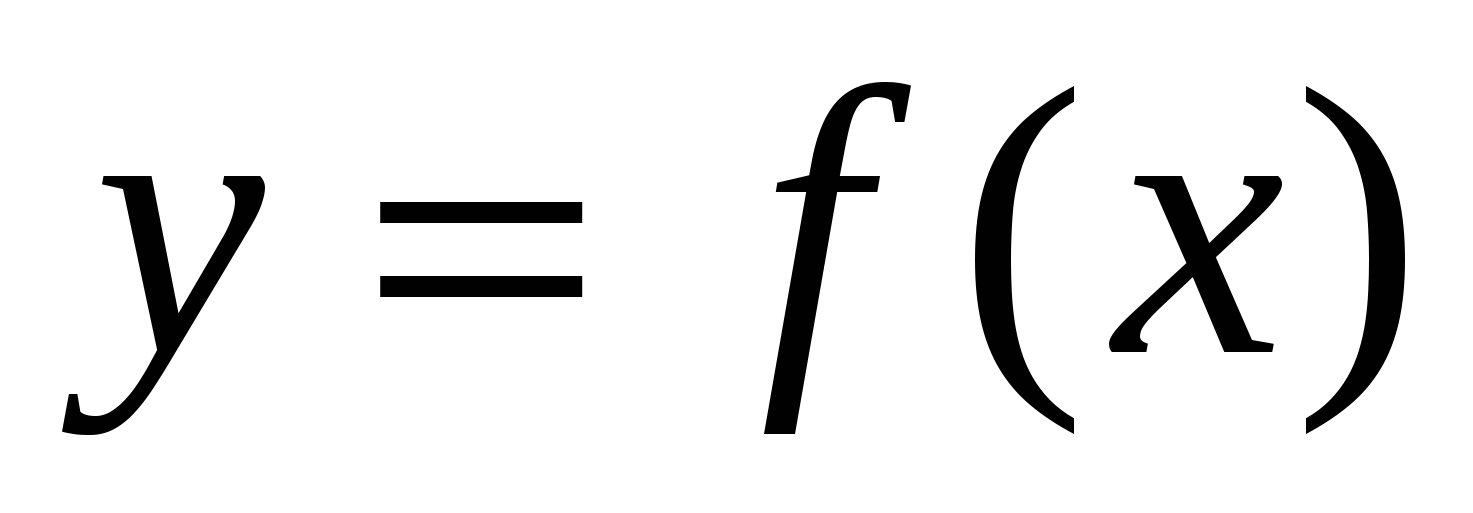 

а)  ;

б)  ;

в)  ;

г)  ;

д) (10,+ ).

11. Функция f(x) возрастает на промежутке (а,в), если на этом промежутке выполняется условие:

а)  0

б)   0