Тест по теме «Векторы в пространстве»
1. Какое из следующих утверждений неверно?
а) длиной ненулевого вектора 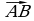 называется длина отрезка АВ;
называется длина отрезка АВ;
б) нулевой вектор считается сонаправленным любому вектору;
в) 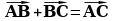 ;
;
г) разностью векторов а и b называется такой вектор. сумма которого с вектором b равна вектору а;
д) векторы называются равными, если равны их длины.
2. Упростите выражение:
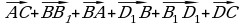 , если ABCDA₁B₁C₁D₁ - параллелепипед.
, если ABCDA₁B₁C₁D₁ - параллелепипед.
а) 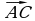 ; б)
; б) 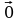 ; в)
; в)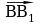 ; г)
; г) 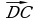 ; д)
; д) 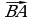 .
.
3. Какое из следующих утверждений верно?
а) сумма нескольких векторов зависит от того, в каком порядке они складываются;
б) противоположные векторы равны;
в) для нахождения разности векторов необходимо, чтобы они выходили из одной точки;
г) произведение вектора на число является число;
д) для любых векторов а и b не выполняется равенство а+b=b+a.
4. Ребро куба ABCDA₁B₁C₁D₁ равно 1. Найдите |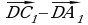 |.
|.
а) 1; б) 2; в) 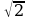 ; г)
; г)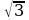 ; д) 0,5
; д) 0,5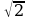 .
.
5. Какое из следующих утверждений неверно?
а) векторы называются компланарными, если при откладывании их от одной и той же точки они будут лежать в одной плоскости;
б) если вектор с можно разложить по векторам а и b, т.е. представить в виде с=ха+yb, где х, y- некоторые числа, то векторы а, b, c компланарны;
в) для сложения трёх некомпланарных векторов используют правило параллелепипеда;
г) любые два вектора компланарны;
д) любые три вектора не компланарны.
6. Известно, что 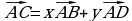 . Тогда прямые АС и ВD:
. Тогда прямые АС и ВD:
а) параллельны; б) пересекаются; в) скрещиваются; г) совпадают;
д) выполняются все условия пунктов а-г.
7. Векторы p, a, b не компланарны, если:
а) при откладывании из одной точки они не лежат в одной плоскости;
б) два из данных векторов коллинеарны; в) один из данных векторов нулевой;
г) p=a – b; д) р=а.
8. ABCDA₁B₁C₁D₁-параллелепипед. Какой из предложенных векторов будет компланарен с векторами 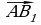 и
и 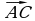 ?
?
а) 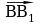 ; б)
; б) 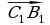 ; в)
; в) 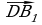 ; г)
; г) 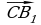 ; д)
; д) 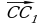 .
.
9.Известно, что 2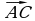 =
=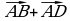 , тогда векторы
, тогда векторы 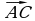 ,
, 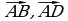 являются:
являются:
а) некомпланарными; б) сонаправленными; в) коллинеарными;
г) нулевыми; д) компланарными.
10. Даны параллелограммы ABCD и AB₁C₁D₁. Тогда векторы 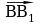 ,
, 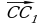 ,
, 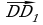 :
:
а) нулевые; б) равные; в) противоположные; г) компланарные; д) некомпланарные.





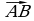 называется длина отрезка АВ;
называется длина отрезка АВ;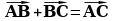 ;
; 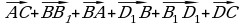 , если ABCDA₁B₁C₁D₁ - параллелепипед.
, если ABCDA₁B₁C₁D₁ - параллелепипед.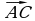 ; б)
; б) 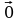 ; в)
; в)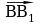 ; г)
; г) 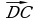 ; д)
; д) 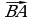 .
.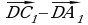 |.
|. 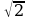 ; г)
; г)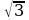 ; д) 0,5
; д) 0,5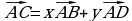 . Тогда прямые АС и ВD:
. Тогда прямые АС и ВD: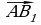 и
и 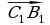 ; в)
; в) 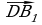 ; г)
; г) 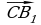 ; д)
; д) 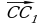 .
.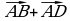 , тогда векторы
, тогда векторы 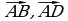 являются:
являются: 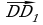 :
:

















