Россия, Бреды, Челябинская обл
СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ
Благодаря готовым учебным материалам для работы в классе и дистанционно
Скидки до 50 % на комплекты
только до
Готовые ключевые этапы урока всегда будут у вас под рукой
Организационный момент
Проверка знаний
Объяснение материала
Закрепление изученного
Итоги урока
Была в сети 26.03.2019 17:19
Воробьева [email protected] Николаевна
учитель математики
62 года
2 069
30 253 
Местоположение
Тест "Теорема синусов, косинусов"
Категория:
Математика
26.03.2019 15:53
Просмотр содержимого документа
«Тест "Теорема синусов, косинусов"»
Л.С. Атанасян. Геометрия 10-11.
Для треугольника АВС справедливо равенство
ПОДУМАЙ!
BC 2 = AB 2 + AC 2 – 2 AB AC cos ABC
1
ВЕРНО!
BC 2 + AC 2
– 2 BC AC
cos BCA
AB 2 =
AB 2 = BC 2 + AC 2 – 2 BC AC cos BCA
2
ПОДУМАЙ!
AC 2 = AB 2 + BC 2 – 2 A B BC cos ACB
3
Квадрат стороны треугольника равен
сумме квадратов двух других сторон
минус удвоенное произведение этих сторон
на косинус угла между ними.
Проверка (4)
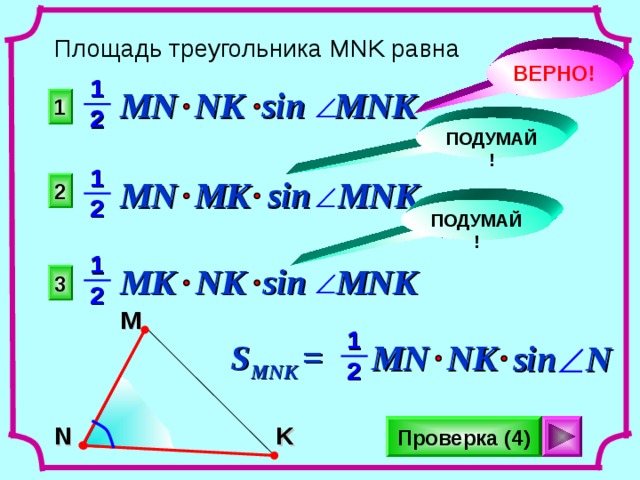
Площадь треугольника MNK равна
ВЕРНО!
1
MN NK sin MNK
1
2
ПОДУМАЙ!
1
MN MK sin MNK
2
2
ПОДУМАЙ!
1
MK NK sin MNK
3
2
M
1
S MNK =
NK
MN
sin N
2
K
N
Проверка (4)
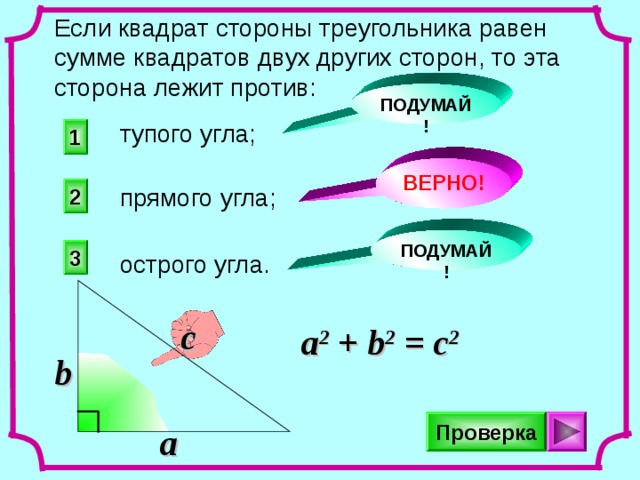
Если квадрат стороны треугольника равен сумме квадратов двух других сторон, то эта сторона лежит против:
ПОДУМАЙ!
тупого угла;
1
ВЕРНО!
прямого угла;
2
ПОДУМАЙ!
3
острого угла.
c
a 2 + b 2 = c 2
b
Проверка
a
В треугольнике АВС известны длины сторон АВ и ВС. Чтобы найти сторону АС, необходимо знать величину:
ВЕРНО!
угла В;
1
A
ПОДУМАЙ!
2
угла С;
n
?
ПОДУМАЙ!
угла А.
3
m
B
C
Проверка
Проверка " width="640"
Треугольник со сторонами 5, 6 и 7 см:
ПОДУМАЙ!
прямоугольный;
1
ПОДУМАЙ!
тупоугольный;
2
ВЕРНО!
3
остроугольный.
Проверка
В треугольнике АВС А = 30 0 , ВС = 3.
Радиус описанной около АВС окружности равен:
ПОДУМАЙ!
1
1,5 ;
ПОДУМАЙ!
2 3;
2
ВЕРНО!
3
3.
Проверка
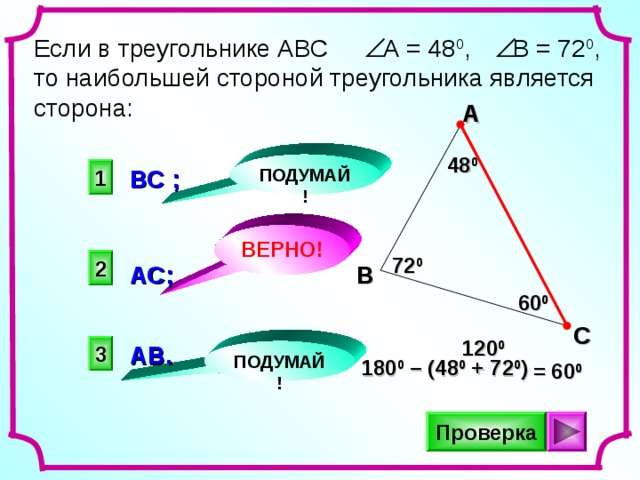
Если в треугольнике АВС А = 48 0 , В = 72 0 , то наибольшей стороной треугольника является сторона:
A
48 0
ПОДУМАЙ!
ВС ;
1
ВЕРНО!
72 0
2
АС;
B
60 0
С
120 0
АВ.
3
ПОДУМАЙ!
180 0 – (48 0 + 72 0 )
= 60 0
Проверка
По теореме синусов:
ВЕРНО!
Стороны треугольника пропорциональны
синусам противолежащих углов.
1
ПОДУМАЙ!
2
Стороны треугольника пропорциональны
противолежащим углам.
ПОДУМАЙ!
3
Стороны треугольника пропорциональны
синусам прилежащих углов.
В треугольнике С DE:
ВЕРНО!
= DE sinE
CD sinC
CD sinC = DE sinE
1
D
ПОДУМАЙ!
CD sinE = DE sinC
2
ПОДУМАЙ!
CD sinD = DE sinE
3
EC
CD
DE
=
=
E
C
sinC
sinE
sinD
Проверка (3)
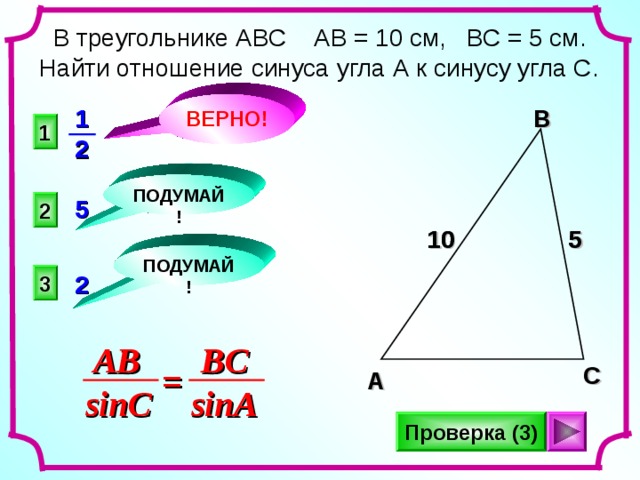
В треугольнике АВС АВ = 10 см, ВС = 5 см. Найти отношение синуса угла А к синусу угла С.
ВЕРНО!
1
В
1
2
ПОДУМАЙ!
5
2
10
5
10
5
ПОДУМАЙ!
3
2
AB
BC
=
С
А
sinA
sinC
Проверка ( 3 )
Вебинар для учителей
Свидетельство об участии БЕСПЛАТНО!
