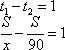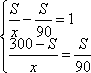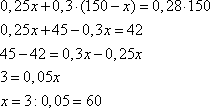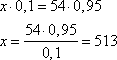Тестовые задачи по математике (с решениями)

Тестовые задачи по математике (с решениями)

В2:Задание 11. Расстояние между городами А и В равно 300 км. Из города А в город В выехал автомобиль, а через 1 час следом за ним со скоростью 90 км/ч выехал мотоциклист, догнал автомобиль в городе С и повернул обратно. Когда он вернулся в А, автомобиль прибыл в В. Найдите расстояние от А до С. Ответ дайте в километрах.

Решение.

Положим, что встреча автомобиля с мотоциклом состоялась на расстоянии в  км от точки A. Соответственно, расстояние от точки встречи C до точки B будет равно  км. За  км/ч примем скорость автомобиля. Тогда, время затраченное автомобилем на прохождение расстояния в  км равно , а время затраченное мотоциклистом . По условию задачи разница во времени у них составила 1 час, т.е.

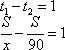
Также по условию задачи сказано, что пока автомобиль ехал  км, мотоциклист за это же время проехал  км, т.е. можно записать равенство

.

Получаем систему из двух уравнений:

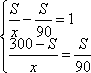
В3:Задание 11. Имеется два сплава. Первый содержит 25 % никеля, второй — 30 % никеля. Из этих двух сплавов получили третий сплав массой 150 кг, содержащий 28% никеля. На сколько килограммов масса первого сплава была меньше массы второго?

Решение.

Обозначим через  массу первого сплава. Масса никеля в этом сплаве 25% или . Масса второго сплава , в котором 30% никеля, т.е. . Третий сплав, равный сумме двух первых сплавов, содержит 150 кг с содержанием никеля 28%, т.е. . В результате получаем уравнение

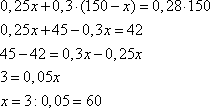
Масса первого сплава равна 60 кг. Масса второго сплава равна  кг. Разница в весе между этими сплавами

90-60=30 кг.

Ответ: 30.

В6

:Задание 11. Изюм получается в процессе сушки винограда. Сколько килограммов винограда потребуется для получения 54 килограммов изюма, если виноград содержит 90% воды, а изюм содержит 5% воды?

Решение.

Сухого вещества изюма в 54 килограммах равно

.

Объем винограда обозначим через . Тогда сухого вещества винограда будет

.

Сухого вещества винограда и изюма должны быть равны, т.е. получаем уравнение

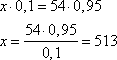
Ответ: 513.

В7:Задание 11. Два гонщика участвуют в гонках. Им предстоит проехать 68 кругов по кольцевой трассе протяжённостью 6 км. Оба гонщика стартовали одновременно, а на финиш первый пришёл раньше второго на 15 минут. Чему равнялась средняя скорость второго гонщика, если известно, что первый гонщик в первый раз обогнал второго на круг через 60 минут? Ответ дайте в км/ч.

Решение.Пусть  - скорость первого гонщика, а  - скорость второго гонщика. Они оба проехали 68 кругов по 6 км каждый круг, т.е. расстояние  км. Время первого гонщика составило , а время второго . Известно, что первый гонщик пришел на 15 минут раньше второго, т.е. на 1/4 часа быстрее, получаем уравнение

.

Также в задаче сказано, что первый гонщик впервые обогнал на круг (на 6 км) второго через 60 минут (1 час), следовательно,

Получаем систему уравнений

Найдем скорость второго гонщика, т.е. y, получим:

подставляем в первое уравнение

в12 Задание 11. Автомобиль выехал с постоянной скоростью 51 км/ч из города А в город В, расстояние между которыми равно 357 км. Одновременно с ним из города С в город В, расстояние между которыми равно 351 км, с постоянной скоростью выехал мотоциклист. По дороге он сделал остановку на 30 минут. В результате автомобиль и мотоцикл прибыли в город В одновременно. Найдите скорость мотоциклиста. Ответ дайте в км/ч.

Решение.

Найдем время, которое затратил мотоциклист на весь путь. Как известно, он приехал в пункт B одновременно вместе с автомобилем, который в свою очередь потратил на путь

 часов.

Учитывая, что мотоциклист делал остановку на 30 минут или 0,5 часа, его время в пути составило

7-0,5=6,5 часа.

Соответственно, скорость мотоциклиста была равна

351:6,5=54 км/ч.

Ответ: 54.

В13 Задание 11. Автомобиль выехал с постоянной скоростью 67 км/ч из города А в город В, расстояние между которыми равно 201 км. Одновременно с ним из города С в город В, расстояние между которыми равно 210 км, с постоянной скоростью выехал мотоциклист. По дороге он сделал остановку на 40 минут. В результате автомобиль и мотоцикл прибыли в город В одновременно. Найдите скорость мотоциклиста. Ответ дайте в км/ч.

Решение.На весь путь автомобиль затратил  часа. Мотоциклист проделал путь в 210 км за  часа. Следовательно, его скорость была равна

 км/ч.

Ответ: 90.

В14 Задание 11. Путешественник переплыл океан на яхте со средней скоростью 26 км/ч. Обратно он летел на самолёте со скоростью 312 км/ч. Найдите среднюю скорость путешественника на протяжении всего пути. Ответ дайте в километрах в час.

Решение.1-й способ. Средняя скорость будет равна, если весь путь разделить на время. На яхте путешественник шел  часов, на самолете летел  часов, следовательно, общее время составило  часов. За это время было пройдено расстояние в , и средняя скорость получается равной

то есть 48 км/ч.

2-й способ. Средняя скорость вычисляется по формуле

Подставляем числовые значения, получаем

 км/ч.

Ответ: 48.

В15 Задание 11. Из пункта А в пункт В одновременно выехали два автомобилиста. Первый проехал с постоянной скоростью весь путь. Второй проехал первую половину пути со скоростью, меньшей скорости первого на 12 км/ч, а вторую половину пути — со скоростью 70 км/ч, в результате чего прибыл в пункт В одновременно с первым автомобилистом. Найдите скорость первого автомобилиста, если известно, что она больше 41 км/ч. Ответ дайте в километрах в час.

Решение.Пусть  - скорость первого автомобилиста. Через  обозначим половину пути между пунктами A и B. Тогда время, затраченное первым автомобилистом на весь путь, равно  часов.

Скорость второго автомобилиста на первой половине равно , а время  часов. Скорость на второй половине пути у второго автомобилиста равна 70 км/ч, следовательно, время составило  часов. Учитывая, что оба автомобилиста преодолели весь путь за одно и то же время, получаем уравнение

Отсюда находим

Решая квадратное уравнение, получаем два корня

По условию задачи скорость первого автомобилиста должна быть больше 41 км/ч, следовательно, его скорость составила 42 км/ч.

Ответ: 42.

В16 Задание 11. Моторная лодка прошла против течения реки 77 км и вернулась в пункт отправления, затратив на обратный путь на 4 ч меньше. Найдите скорость лодки в неподвижной воде, если скорость течения равна 2 км/ч. Ответ дайте в километрах в час.

Решение.Пусть скорость моторной лодки в неподвижной воде равна  км/ч. Тогда скорость лодки против течения будет равна  км/ч. Расстояние в 77 км лодка преодолеет с такой скоростью за  часа. На обратном пути лодка шла по течению, следовательно, со скоростью  км/ч и прошла 77 км за  часа. В задаче сказано, что на обратный путь было потрачено на 4 часа меньше, получаем уравнение

Решаем уравнение, имеем:

Так как скорость лодки должна быть положительной, получаем ответ 9 км/ч.

Ответ: 9.

В17 Задание 11. Коля и Митя выполняют одинаковый тест. Коля отвечает за час на 12 вопросов теста, а Митя — на 21. Они одновременно начали отвечать на вопросы теста, и Коля закончил свой тест позже Мити на 105 минут. Сколько вопросов содержит тест?

Решение.Пусть в тесте  вопросов. Тогда общее время ответа Коли на все вопросы равно  часов, а общее время ответа Мити  часов. Известно, что Коля отвечал на тест на 105 минут (7/4 часа) дольше Мити. Имеем уравнение

То есть в тесте 49 вопросов.

Ответ: 49.

В18 Задание 11. Костя и Гриша выполняют одинаковый тест. Костя отвечает за час на 12 вопросов теста, а Гриша — на 20. Они одновременно начали отвечать на вопросы теста, и Костя закончил свой тест позже Гриши на 90 минут. Сколько вопросов содержит тест?

Решение.Обозначим через  общее число вопросов в тесте. Тогда общее время ответа на все вопросы у Кости составит  часов, а у Гриши  часов. Известно, что Костя отвечал дольше Гриши на 90 минут (3/2 часа), получаем уравнение:

То есть в тесте 45 вопросов.

Ответ: 45.

Задание 11. Игорь и Паша красят забор за 18 часов. Паша и Володя красят этот же забор за 24 часа, а Володя и Игорь — за 36 часов. За сколько часов мальчики покрасят забор, работая втроём?

Решение.Пусть за  часов красит забор Игорь, за  часов - Паша, а за  часов Володя. Весь забор условно примем за одну целую часть, т.е. за 1. Тогда условная скорость покраски забора Игорем составляет , для Паши , а для Володи . В задаче сказано, что Игорь и Паша вместе красят забор за 18 часов, т.е. можем записать уравнение

.

Аналогично для Паши и Володи

и Володи и Игоря

.

Получаем систему из трех уравнений

Складывая все эти три уравнения получаем

То есть все втроем покрасят забор за 16 часов.

Ответ: 16.

Задание 11. Моторная лодка прошла против течения реки 55 км и вернулась в пункт отправления, затратив на обратный путь на 6 ч меньше. Найдите скорость лодки в неподвижной воде, если скорость течения равна 3 км/ч. Ответ дайте в километрах в час.

Решение.Обозначим через  скорость лодки в неподвижной воде. Вначале лодка шла против течения 55 км, следовательно, затраченное на весь путь время составило  часов. На обратный путь (движение по течению) было затрачено  часа. В задаче сказано, что обратный путь было на 6 часов меньше, имеем уравнение

откуда получаем

Так как скорость не должна быть отрицательной величиной, то получаем ответ 8 км/ч.

Ответ: 8.

В21 Задание 11. Из пункта А в пункт В, расстояние между которыми 60 км, одновременно выехали автомобилист и велосипедист. Известно, что в час автомобилист проезжает на 25 км больше, чем велосипедист. Определите скорость велосипедиста, если известно, что он прибыл в пункт В на 2 часа 30 минут позже автомобилиста. Ответ дайте в километрах в час.

Решение.Обозначим через  скорость велосипедиста. Тогда время, затраченное на путь в 60 км будет равно  часов. Скорость автомобиля на 25 км/ч больше скорости велосипеда и равна . Следовательно, время затраченное на путь в 60 км автомобилем будет равно  часов. Известно, что велосипедист затратил на весь путь на 2 часа 30 минут (5/2 часа) больше времени, чем автомобилист. Имеем уравнение

откуда получаем

Решаем квадратное уравнение, получаем два корня

Так как скорость должна быть положительной, то получаем ответ 15 км/ч.

Ответ: 15.

В22 Задание 11. Игорь и Паша красят забор за 12 часов. Паша и Володя красят этот же забор за 15 часов, а Володя и Игорь — за 20 часов. За сколько часов мальчики покрасят забор, работая втроём?

Решение.Пусть за  часов красит забор Игорь, за  часов красит забор Паша и за  часов красит забор Володя. Весь забор условно примем за 1. Тогда скорость покраски забора Игорем составит , Пашей , а вдвоем они красят забор со скоростью . Получаем уравнение

.

Аналогично получаем для Паши и Володи

и для Володи и Игоря

.

Имеем систему из трех уравнений

Складывая все эти три уравнения, имеем:

То есть втроем они покрасят забор за 10 часов.

Ответ: 10.

В23 Задание 11. Из одной точки круговой трассы, длина которой равна 25 км, одновременно в одном направлении стартовали два автомобиля. Скорость первого автомобиля равна 112 км/ч, и через 25 минут после старта он опережал второй автомобиль на один круг. Найдите скорость второго автомобиля. Ответ дайте в км/ч.

Решение.В задаче сказано, что через 25 минут (5/12 часа) первый автомобиль обогнал второй на 1 круг, т.е. на 25 км. Следовательно, скорость первого автомобиля выше скорости второго на

 км/ч.

Таким образом, скорость второго равна 112-60=52 км/ч.

Ответ: 52.

В24 Задание 11. Валя и Галя пропалывают грядку за 8 минут, а одна Галя — за 10 минут. За сколько минут пропалывает грядку одна Валя?

Решение.Условно, всю грядку примем за 1, а время прополки грядки Валей примем за . Тогда, скорость прополки всей грядки Валей составит , а Галей . Известно, что вдвоем они пропалывают грядку за 8 минут. Получаем уравнение

Откуда находим

то есть за 40 минут.

Ответ: 40.

В25 Задание 11. Из пункта А в пункт В, расстояние между которыми 60 км, одновременно выехали автомобилист и велосипедист. Известно, что в час автомобилист проезжает на 30 км больше, чем велосипедист. Определите скорость велосипедиста, если известно, что он прибыл в пункт В на 2 часа 40 минут позже автомобилиста. Ответ дайте в километрах в час.

Решение.Обозначим через  скорость велосипедиста. В задаче сказано, что автомобиль движется со скоростью на 30 км/ч быстрее велосипедиста, т.е. его скорость равна . Автомобиль весь путь в 60 км проезжает за  часов. Велосипедист проедет этот же путь за  часов. Известно, что велосипедист приехал на 2 часа 40 минут (8/3 часа) позже автомобилиста. Получаем уравнение

Откуда имеем

Решаем квадратное уравнение, получаем два корня

Так как скорость должна быть положительной в данной задаче, то получаем ответ 15 км/ч.

Ответ: 15.

В26 Задание 11. Первая труба пропускает на 1 л воды в минуту меньше, чем вторая. Сколько литров воды в минуту пропускает вторая труба, если резервуар объёмом 110 л она заполняет на 1 мин быстрее, чем первая труба?

Решение.Пусть  литров воды пропускает вторая труба в минуту. Тогда первая труба будет пропускать  литров воды. Скорость наполнения первой трубой резервуара в 110 литров равна , а второй трубой . В задаче сказано, что вторая труба заполняет резервуар в 110 л быстрее первой на 1 минуту. Получаем уравнение

Имеем

Решаем квадратное уравнение, получаем корни

Так как скорость наполнения должна быть положительной, то получаем ответ 11 литров в минуту.

Ответ: 11.

В27 Задание 11. По двум параллельным железнодорожным путям в одном направлении следуют пассажирский и товарный поезда, скорости которых равны соответственно 80 км/ч и 50 км/ч. Длина товарного поезда равна 1200 метрам. Найдите длину пассажирского поезда, если время, за которое он прошёл мимо товарного поезда, равно 3 минутам. Ответ дайте в метрах.

Решение.Скорость обгона пассажирским поездом товарного составляет 80-50=30 км/ч. Товарный поезд имеет длину 1200 метров или 1,2 км. В задаче сказано, что пассажирский поезд прошел мимо товарного за 3 минуты (за 1/20 часа) со скоростью 30 км/ч. То есть была пройдена вся длина товарного поезда и еще длина самого пассажирского поезда. Обозначим через  длину пассажирского поезда, тогда расстояние равное  было пройдено за 1/20 часа со скоростью 30 км/ч. Получаем уравнение

Откуда имеем

То есть длина пассажирского поезда равна 0,3 км или 300 метров.

Ответ: 300.

В28 Задание 11. Первая труба пропускает на 1 л воды в минуту меньше, чем вторая. Сколько литров воды в минуту пропускает вторая труба, если резервуар объёмом 870 л она заполняет на 1 мин быстрее, чем первая труба?

Решение.Пусть  пропускная способность второй трубы. Тогда первая труба будет иметь пропускную способность . Резервуар объемом 870 литров первая труба будет наполнять  минут, а вторая  минут. По условию задачи вторая труба наполняет резервуар на 1 минуту быстрее, чем первая. Получаем уравнение

откуда имеем

Решаем квадратное уравнение, получаем два корня

Так как пропускная способность должна быть положительным числом, то получаем ответ 30.

Ответ: 30.

В29 Задание 11. По двум параллельным железнодорожным путям друг навстречу другу следуют скорый и пассажирский поезда, скорости которых равны соответственно 80 км/ч и 40 км/ч. Длина пассажирского поезда равна 350 метрам. Найдите длину скорого поезда, если время, за которое он прошёл мимо пассажирского поезда, равно 24 секундам. Ответ дайте в метрах.

Решение.Обозначим через  длину скорого поезда. Так как поезда движутся навстречу друг другу, то скорость прохождения поездов мимо друг друга составляет 80+40=120 км/ч. В задаче сказано, что поезда прошли мимо друг друга за 24 секунды (24/3600 часа). Это эквивалентно тому, что скорый поезд прошел за это время 350 метров (0,35 км) и еще свою длину. Получаем уравнение

откуда имеем

То есть длина скорого поезда 0,45 км или 450 метров.

Ответ: 450.

В30 Задание 11. Путешественник переплыл океан на яхте со средней скоростью 30 км/ч. Обратно он летел на самолёте со скоростью 570 км/ч. Найдите среднюю скорость путешественника на протяжении всего пути. Ответ дайте в километрах в час.

Решение.Среднюю скорость движения можно найти по формуле

.

Подставим вместо , вместо , получим

 км/ч.

Ответ: 57.

В31 Задание 11. Имеется два сплава. Первый содержит 5% никеля, второй — 25% никеля. Из этих двух сплавов получили третий сплав массой 250 кг, содержащий 20% никеля. На сколько килограммов масса первого сплава была меньше массы второго?

Решение.Обозначим через  массу первого сплава. Тогда масса второго сплава будет равна . Масса никеля в первом сплаве равна , масса никеля во втором сплаве равна . Учитывая, что масса никеля в третьем сплаве равна , получаем уравнение

То есть масса первого сплава равна 62,5 кг. Масса второго сплава равна

250-62,5=187,5 кг.

Разница в массе этих сплавов составляет

187,5-62,5=125 кг.

Ответ: 125.

В32 Задание 11. Смешали некоторое количество 11-процентного раствора некоторого вещества с таким же количеством 15-процентного раствора этого вещества. Сколько процентов составляет концентрация получившегося раствора?

Решение.Массу раствора обозначим через , тогда в первом растворе количество вещества составляет , а во втором - . В сумме эти два раствора дают процентный состав вещества равный . Найдем величину  из уравнения

То есть в получившемся растворе концентрация составит 13%.

Ответ: 13.

в33 Задание 11. Теплоход проходит по течению реки до пункта назначения 780 км и после стоянки возвращается в пункт отправления. Найдите скорость течения, если скорость теплохода в неподвижной воде равна 28 км/ч, стоянка длится 4 ч, а в пункт отправления теплоход возвращается через 60 ч после отплытия из него. Ответ дайте в километрах в час.

Решение.Пусть  км/ч скорость течения реки. Теплоход сначала двигался по течению и его скорость составила  км/ч. Затем, на обратном пути он двигался против течения со скоростью  км/ч. Время, проведенное в пути составило  - по течению,  - против течения и 4 часа на стоянке. В сумме это время равнялось 60 часов. Имеем уравнение

или в виде

Преобразуем его к виду

Получили скорость течения реки 2 км/ч.

Ответ: 2.

В34 Задание 11. Имеется два сплава. Первый содержит 5% меди, второй — 11% меди. Масса второго сплава больше массы первого на 8 кг. Из этих двух сплавов получили третий сплав, содержащий 10% меди. Найдите массу третьего сплава. Ответ дайте в килограммах.

Решение.Пусть  масса первого сплава. Масса второго сплава на 8 кг больше, т.е. . Масса меди в первом сплаве равна , а во втором . В сумме эти два сплава дают третий сплав с содержанием меди 10%, т.е.

.

Получаем уравнение

Масса сплава определяется выражением  и равна

 кг.

Ответ: 12.

В35 Задание 11. Имеется два сплава. Первый содержит 5% никеля, второй — 30% никеля. Из этих двух сплавов получили третий сплав массой 100 кг, содержащий 20% никеля. На сколько килограммов масса первого сплава была меньше массы второго?

Решение.Обозначим через  массу первого сплава. Масса двух сплавов равна 100, следовательно, масса второго сплава равна . В первом сплаве масса никеля равна , а во втором сплаве . В результирующем сплаве доля никеля составляет 20%, т.е. . Получаем уравнение

Масса второго сплава равна 100-40=60 кг. Следовательно, разность между двумя сплавами составляет

60-40=20 кг.

Ответ: 20.

В36 Задание 11. Имеется два сосуда. Первый содержит 80 кг, а второй — 70 кг раствора кислоты различной концентрации. Если эти растворы смешать, то получится раствор, содержащий 63% кислоты. Если же смешать равные массы этих растворов, то получится раствор, содержащий 65% кислоты. Сколько килограммов кислоты содержится в первом сосуде?

Решение.Обозначим через  концентрацию первого раствора, а через  - концентрацию второго раствора. Первый раствор имеем массу 80 кг, следовательно, кислоты в нем , а второй 70 кг с массой кислоты . Известно, что в сумме они дают концентрацию 63%, т.е.  кг. Имеем уравнение

.

Также сказано, что при смешивании равных масс растворов, получается третий с концентрацией 65%:

.

Получаем систему линейных уравнений:

Решаем систему уравнений. Второе уравнение умножим на -70 и оба уравнения сложим, получим

Умножим левую и правую части уравнения на 8, получим соотношение

,

что соответствует концентрации кислоты в 80 кг раствора.

Ответ: 28.

В2 Задание 10. Для получения на экране увеличенного изображения лампочки в лаборатории используется собирающая линза с главным фокусным расстоянием f = 30 см. Расстояние d1 от линзы до лампочки может изменяться в пределах от 25 до 50 см, а расстояние d2 от линзы до экрана — в пределах от 90 до 120 см. Изображение на экране будет четким, если выполнено соотношение   .

Укажите, на каком наименьшем расстоянии от линзы нужно поместить лампочку, чтобы её изображение на экране было чётким. Ответ выразите в сантиметрах.

Решение.По условию задачи нужно найти наименьшее расстояние  между линзой и лампочкой, такое, чтобы изображение было четким. Для нахождения минимального  преобразуем выражение

Фокусное расстояние , расстояние  принимает минимальное значение 90 и максимальное 120. Рассчитаем расстояние  при разных граничных значениях , получим:

- для :

;

- для :

.

Минимальное расстояние равно 40.

Ответ: 40.

В6 Задание 10. Локатор батискафа, равномерно погружающегося вертикально вниз, испускает ультразвуковые импульсы частотой 299 МГц. Скорость спуска батискафа, выражаемая в м/с, определяется по формуле , где с = 1500 м/с — скорость звука в воде, f0 — частота испускаемых импульсов (в МГц), f — частота отражённого от дна сигнала, регистрируемая приёмником (в МГц). Определите наибольшую возможную частоту отражённого сигнала f, если скорость погружения батискафа не должна превышать 5 м/с. Ответ выразите в МГц.

Решение.Так как скорость батискафа не превышает 5 м/с, то получаем неравенство

и, подставляя числовые значения, получаем

Таким образом, наибольшее значение равно 301 МГц.

Ответ: 301.

В7 Задание 10. Высота над землёй подброшенного вверх мяча меняется по закону , где h — высота в метрах, t — время в секундах, прошедшее с момента броска. Сколько секунд мяч будет находиться на высоте не менее 10 м?

Решение.На высоте не менее 10 метров означает, что , получаем неравенство

Решаем квадратное уравнение, получаем два корня

Таким образом, мяч будет находиться на высоте не менее 10 метров

1,6-1=0,6 секунд.

Ответ: 0,6.

В9 Задание 10. Зависимость объёма спроса q (единиц в месяц) на продукцию предприятия-монополиста от цены р (тыс. руб.) задаётся формулой q = 140-10p. Выручка предприятия за месяц r (тыс. руб.) вычисляется по формуле r(p) = pq. Определите наибольшую цену р, при которой месячная выручка r(p) составит 400 тыс. руб. Ответ приведите в тысячах рублей.

Решение.Из равенства  выразим , учитывая, что , получим:

Выручка , следовательно,

Решаем квадратное уравнение, получаем два корня

Наибольшая цена равна 10 тыс. руб.

Ответ: 10.

В11 Задание 10. Самые красивые мосты — вантовые. Вертикальные пилоны связаны огромной провисающей цепью. Тросы, которые свисают с цепи и поддерживают полотно моста, называются вантами.

На рисунке изображена схема одного вантового моста. Введём систему координат: ось Оу направим вертикально вдоль одного из пилонов, а ось Ох направим вдоль полотна моста, как показано на рисунке. В этой системе координат цепь моста имеет уравнение , где х и у измеряются в метрах. Найдите длину ванты, расположенной в 100 метрах от пилона. Ответ дайте в метрах.

Решение.

Длина ванты, расположенной в 100 метрах от пилона будет равна значению функции  в точке , получим:

Ответ: 8,6.

В14 Задание 10. В ходе распада радиоактивного изотопа его масса уменьшается по закону , где m0 — начальная масса изотопа, t (мин) — прошедшее от начального момента время, Т (мин) — период полураспада. В лаборатории получили вещество, содержащее в начальный момент времени m0 = 4 мг изотопа Z, период полураспада которого Т = 2 мин. Через какое время после начала распада масса изотопа станет меньше 1 мг?

Решение.Необходимо определить время  через которое масса , получим неравенство

Подставляем числовые значения, имеем:

То есть через 4 секунды.

Ответ: 4.

В15 Задание 10. При адиабатическом процессе для идеального газа выполняется закон , где р — давление в газе в паскалях, V — объём газа в кубических метрах. В ходе эксперимента с одноатомным идеальным газом (для него k = 4/3) из начального состояния, в котором  Па•м4, газ начинают сжимать. Какой наибольший объём V может занимать газ при давлениях р не ниже  Па? Ответ выразите в кубических метрах.

Решение.Давление должно быть . Тогда из равенства   имеем

Перейдем к неравенству, получим:

Таким образом, получаем, что наибольшее значение объема равно 8.

Ответ: 8.

В16 Задание 10. Рейтинговое агентство вычисляет рейтинг интернет-магазинов по формуле

,

где  — средняя оценка магазина покупателями (от 0 до 1),  — оценка магазина экспертами компании (от 0 до 0,7) и К — число покупателей, оценивших магазин.

Найдите рейтинг интернет-магазина «Альфа», если число покупателей, оставивших отзыв о магазине, равно 24, их средняя оценка равна 0,38, а оценка экспертов равна 0,13.

Решение.По условию задачи дано , , . Подставим эти данные в выражение для вычисления рейтинга. Сначала вычислим степень у параметра , получим:

И рейтинг равен

Ответ: 0,37.

В17 Задание 10. При температуре 0°С рельс имеет длину  = 10 м. При возрастании температуры происходит тепловое расширение рельса, и его длина, выраженная в метрах, меняется по закону , где  — коэффициент теплового расширения, t° — температура (в градусах Цельсия). При какой температуре рельс удлинится на 9 мм? Ответ выразите в градусах Цельсия.

Решение.Необходимо рассчитать значение , при котором  метров. Воспользуемся законом изменения длины рельс от температуры и выразим температуру, получим:

Ответ: 75.

В21 Задание 10. Для получения на экране увеличенного изображения лампочки в лаборатории используется собирающая линза с главным фокусным расстоянием f = 35 см. Расстояние d1 от линзы до лампочки может изменяться в пределах от 35 до 60 см, а расстояние d2 от линзы до экрана — в пределах от 240 до 280 см. Изображение на экране будет чётким, если выполнено соотношение . Укажите на каком наименьшем расстоянии от линзы можно поместить лампочку, чтобы её изображение на экране было чётким. Ответ выразите в сантиметрах.

Решение.

Нужно найти наименьшее значение , при котором изображение лампочки будет четким. Выразим  из соотношения , получим:

Максимальное расстояние для , в этом случае величина  будет равна

,

а при величине 

,

следовательно, минимальное расстояние равно 40 см.

Ответ: 40.

В22 Задание 10. Небольшой мячик бросают под острым углом  к плоской горизонтальной поверхности земли. Максимальная высота полёта мячика, выраженная в метрах, определяется формулой , где v0 = 26 м/с — начальная скорость мячика, а g — ускорение свободного падения (считайте g = 10 м/с2). При каком наименьшем значении угла а (в градусах) мячик пролетит над стеной высотой 7,45 м на расстоянии 1 м?

Решение.Чтобы найти наименьшее значение угла, нужно в выражение закона полета мяча подставить ту высоту, которая дана в задаче и, соответственно, все остальные числовые значения. Выразим сначала косинус двойного угла из закона движения мяча, получим:

Подставим сюда числовые значения

Ответ: 30.

В23 Задание 10. При адиабатическом процессе для идеального газа выполняется закон , где р — давление в газе в паскалях, V — объём газа в кубических метрах. В ходе эксперимента с одноатомным идеальным газом (для него k=5/3) из начального состояния, в котором  Па•м5, газ начинают сжимать. Какой наибольший объём V может занимать газ при давлениях р не ниже  Па? Ответ выразите в кубических метрах.

Решение.Из закона для идеального газа  можем записать

По задаче необходимо обеспечить давление не ниже  Па, получаем неравенство

откуда

Это неравенство показывает, что наибольший объем равен 0,008 куб. метров.

Ответ: 0,008.