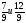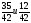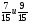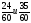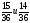закрепить знание основного свойства дроби и умения сокращать дроби.
| Этап урока | Цель | Содержание учебного материала | Методы и приёмы работы | ФОУД | Деятельность учителя | Деятельность обучающихся |
| Мотивация (самоопределение) к учебной деятельности | Создать благоприятный психологический настрой на работу | Приветствие детей, познакомить со структурой урока. Узнать настрой детей на урок с помощью смайликов. Чтобы легче всем жилось, Чтоб решалось, чтоб моглось, Улыбнись, удача всем, Чтобы не было проблем. Давайте улыбнёмся друг другу, создадим хорошее настроение и начнём урок. |
| Ф | Приветствие, проверка подготовленности к учебному занятию, организация внимания детей | Включаются в деловой ритм урока |
| Актуализация и фиксирование индивидуального затруднения в пробном действии | Актуализация опорных знаний и способов действий | 1. Что называется наибольшим общим делителем чисел? 2.Найдите наибольший общий делитель чисел 9 и 12; 15 и 25; 12 и 16; 7 и 14. 3.Что называется наименьшим общим кратным? 4.Найдите наименьшее общее кратное чисел 12 и 16; 3 и 4; 6 и 18. 3. Укажите верное равенство  На основании какого свойства вы это определили? На основании какого свойства вы это определили? 4. Восстановите запись а) 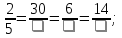 б) б)  Что можно сказать об этих дробях? Что можно сказать об этих дробях? |
| Ф | Организация устного счета и повторения понятий НОД и НОК числа, сокращение дробей. | Участвуют в работе по повторению: в беседе с учителем отвечают на поставленные вопросы. |
| Выявление места и причины затруднения | Обсуждение необходимости введения нового знания | Кролик и ёжик нашли мешок моркови. Каждому хочется взять побольше. По дороге шёл медведь, который помог им решить эту проблему: ежу досталось 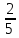 мешка, а кролику мешка, а кролику 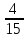 мешка моркови. Кому из них досталось больше? мешка моркови. Кому из них досталось больше? Сразу определить нельзя, надо найти способ решения этой проблемы. Можно сравнивать, если привести к общему знаменателю. | Метод сравнения, анализа, представления |
Ф | Выводит учащихся на формулировку темы и целей урока. Четко проговаривает тему и цель урока. | Сравнивают дроби. Выходят на необходимость получения новых знаний. |
| Построение проекта выхода из затруднения | Координирование деятельности учащихся в группах | Применяя основное свойство дроби сравните дроби: Запишите дробь 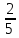 и приведите её к знаменателю 35, 20. Как мы это сделаем? и приведите её к знаменателю 35, 20. Как мы это сделаем? А к какому знаменателю можно привести 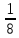 и и 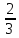 . Какой наименьший знаменатель? . Какой наименьший знаменатель? | Частично- поисковый | Коллект. | Организация и контроль за работой в группах | Проговаривают алгоритм выполнения действий ; на конкретных примерах учатся их применять Устанавливают рабочие отношения, учатся эффективно сотрудничать и способствовать эффективной работе в группе. |
| Реализация построения проекта | Знакомство и фиксирование новых понятий. Составление алгоритма приведения дробей к общему знаменателю. | Составим алгоритм приведения дробей к общему знаменателю: Найти НОК знаменателей данных дробей, которое и будет общим знаменателем. Найдем для каждой дроби дополнительный множитель. Для этого разделим общий знаменатель на знаменатели данных дробей. Умножим числитель и знаменатель каждой дроби на ее дополнительный множитель. |
Деятельностный метод, метод самоконтроля. |
Ф | Является модератором работы в группах. | Планируют алгоритм выполнения задания, корректируют работу по ходу выполнения с помощью учителя. |
| Физкультминутка | Смена деятельности | Физкультминутка проводится под музыкальное сопровождение |
|
Коллект. | Сменить деятельность, обеспечить эмоциональную разгрузку учащихся | Учащиеся сменили вид деятельности и готовы продолжить работу |
| Первичное закрепление с проговариванием во внешней речи | Формирование навыка применения алгоритма приведения дробей к общему знаменателю. | Работа с учебником. стр. 45 № 275 (а, б) с проговариванием во внешней речи.
|
Метод наблюдения. | Ф | Организация работы учащихся по выполнению №275(а,б) с проговариванием во внешней речи; с последующей проверкой ответов и алгоритма рассуждений | Проговаривают алгоритм выполнения действий ; на конкретных примерах учатся их применять |
| Самостоятельная работа с самопровкркой | Формирование навыка применения алгоритма приведения дробей к общему знаменателю. | Работа с учебником. стр. 46 № 281 (б) один ученик работает на оборотной стороне доски, остальные в тетради. | Метод самооценки. | И | Организация работы по выполнению заданий с последующей проверкой. | самостоятельно выполняют действия по алгоритму, контролируют свои действия. |
| Самостоятельная работа с самопроверкой по доске. | Обеспечение усвоения алгоритма выполнения заданий с обыкновенными дробями. | Работа с учебником. стр. 46 № 283 (1 столбик) у доски и в тетрадях |
Метод взаимоконтроля. |
И | Организация работы по выполнению заданий с последующей проверкой (проверка тетради соседа). | самостоятельно выполняют действия по алгоритму; проявляют познавательную инициативу, контролируют знания соседа. |
| Самостоятельная работа с самопроверкой | Проверка усвоения выполнения заданий с обыкновенными дробями | Приведите дроби к наименьшему общему знаменателю, у вас на партах таблица для ответов, выполните решение в тетради, а в таблицу запишите дроби с новыми знаменателями. 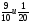    а) ; б) ; а) ; б) ; 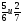 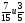 в) ; г) ; в) ; г) ; 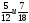  д) ; ; е) ; д) ; ; е) ; ж) ; з) . А теперь проверьте свои ответы по данной таблице:
Какая пара выполнила без ошибок? Молодцы! Хорошо! А кто с одной ошибкой? А те, у кого не получилось выполнить без ошибок, не переживайте, мы только начинаем изучать тему и вы ее отработаете на следующих уроках. | Метод наблюдения, самоконтроля. |
П | Организует работу в парах | Учащиеся работают в парах, делят выполнение заданий, проговаривают друг другу алгоритм и выполняют работу |
| Задание на дом | Организация самооценки учениками собственной учебной деятельности | 1 группа: у кого всё правильно: составить задачу на приведение дробей к общему знаменателю; 2 группа: у кого 1 или 2 ошибки: № 300; 3 группа: остальным № 297, 300(а). | Метод самооценки | Ф | Устанавливает качество усвоения знаний | Записывают задание на дом. |
| Включение в систему знаний и повторение | Обеспечение осознания учащимися своей учебной деятельности на уроке | Давайте подведём итоги. Что нового вы узнали на уроке? Чему научились? С какими новыми понятиями сегодня познакомились? (общий знаменатель, дополнительный множитель) Какое число может служить общим знаменателем двух дробей? |
Систематизация, диалог. |
Ф | Выявляет качество и уровень усвоения знаний, а также устанавливает причины выявленных ошибок. | Учащиеся анализируют свою работу, выражают вслух свои затруднения и обсуждают правильность. |
| Рефлексия учебной деятельности | Оценивать правильность выполнения действия | Мне сегодня было очень приятно с вами работать. Улыбки у вас сохранились?  У вас на столе лежат смайлики. Возьмите тот из них, которое показывает ваше настроение.
|
Метод рефлексии |
Ф | Организует самооценку учебной деятельности. | Рассказывают , что знают и что узнали. Дают самооценку. |
| Дополнительная информация |
| Каким образом данный урок будет содействовать реализации новых ФГОС | формирование коммуникативных УУД, включающих умения высказывать суждения с использованием математических терминов и понятий таких, как наименьший общий знаменатель, дополнительный множитель. формирование познавательных УУД - основных мыслительных операций в ходе составления алгоритма приведения дробей к общему знаменателю. формирование регулятивных действий - действий контроля, включающих приёмы самопроверки и взаимопроверки, умений самостоятельно двигаться по заданному плану, оценивать и корректировать полученный результат.
|
| Ресурсы, оборудование и материалы | Презентация на этапе актуализация знаний и умений, самостоятельная работа с самопроверкой, рефлексия. |
| Список учебной и дополнительной литературы | Математика. 6 класс: учебник для общеобразовательных учреждений. Н.Я. Виленкин, В.И. Жохов и др.-М.:Мнемозина, 2013. |
| Ссылки на использованные интернет-ресурсы |
|
| Дидактическое обеспечение урока ССЫЛКИ | Дидактические материалы по математике для 6 класса. А.С. Чесноков и К.И. Нешков.- М.: Просвещение, 2015. |
| Используемые педагогические технологии, методы и приемы | Проблемного обучения, здоровьесберегающие, технология развития критического мышления через чтение и письмо. |







 На основании какого свойства вы это определили?
На основании какого свойства вы это определили?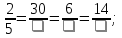 б)
б)  Что можно сказать об этих дробях?
Что можно сказать об этих дробях?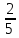 мешка, а кролику
мешка, а кролику 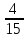 мешка моркови. Кому из них досталось больше?
мешка моркови. Кому из них досталось больше?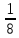 и
и 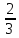 . Какой наименьший знаменатель?
. Какой наименьший знаменатель?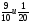


 а) ; б) ;
а) ; б) ; 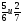
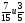 в) ; г) ;
в) ; г) ; 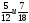
 д) ; ; е) ;
д) ; ; е) ;