Теория и методика развития математических представлений у детей дошкольного возраста
1.Понятие множества и элемента множества
Определение. Множество - набор, совокупность, собрание каких-либо объектов, называемых его элементами, обладающих общим для всех их характеристичным свойством.
Множество – одно из основных понятий современной математики, используемое почти во всех ее разделах.
Информация для понимания, примеры. Во многих вопросах приходится рассматривать некоторую совокупность элементов как единое целое. Так, биолог, изучая животный мир и растительный мир данной области, классифицирует все особи по видам, виды по родам. Каждый вид является некоторой совокупность живых существ, рассматриваемой как единое целое.
Для математического описания таких совокупностей и было введено понятие множества (например, это значит, что можно говорить о множестве чисел от 1 до 10, натуральных числах, множестве треугольников и квадратов на плоскости).
Понятие множества является одним из основных понятий математики и поэтому не определяется через другие. Его можно пояснить на примерах. Так, можно говорить о множестве учащихся некоторого класса, о множестве гласных букв русского алфавита, о множестве натуральных чисел. В математике рассматривают множество, состоящее из одного объекта, и множество, не содержащее ни одного объекта.
Множества обозначают буквами латинского алфавита: A,B,C, …,Z,L.
Определение. Множество, не содержащее ни одного объекта, называют пустым и обозначают знаком .
Определение. Объекты, из которых образовано множество, называют его элементами.
Элементы множества принято обозначать строчными буквами латинского алфавита: a, b, c, …, z.
В математике и других науках нередко приходится выяснять, принадлежит какой-либо объект рассматриваемому множеству или не принадлежит.
Примеры. Предложение вида “ Объект а принадлежит множеству А” можно записать, используя символы: аА. Прочитать его можно по-разному:
Объект а принадлежит множеству А.
Объект а – элемент множества А.
Множество А содержит элемент а.
Предложение “ Объект а не принадлежит множеству А” можно записать так: а А. Его читают:
Объект а не принадлежит множеству А.
Объект а не является элементом множества А.
Множество А не содержит элемента а.
Например
1) Пусть А – множество однозначных чисел. Тогда предложение “7А” можно прочитать: “Число 7 однозначное”, а запись “ 14 А” означает: “Число 14 не является однозначным”.
2) Пусть N – множество натуральных чисел. Тогда предложение «5N» можно прочитать как число 5 - натуральное. Другими словами, число 5 принадлежит множеству натуральных чисел. Или, например, число 0,45 не является натуральным числом. Это означает, что число 0,45 не принадлежит множеству натуральных чисел.
Множества бывают конечными и бесконечными. Так, множество дней недели конечно, а множество точек прямой бесконечно.
3) Пример бесконечных множеств. Бесконечными множествами являются множество натуральных чисел (N), множество целых чисел (Z), множество рациональных чисел (Q), множество действительных чисел (R).
2. Способы задания множеств.
Первый способ. Перечислив все элементы множества, мы создадим множество.
Пример №1 : множество А состоит из чисел 3, 4, 5 и 6. Поскольку все его элементы окажутся перечисленными, то это множество задано. При этом возможна запись А = 3, 4, 5, 6, в которой перечисленные элементы заключаются в фигурные скобки.
Пример №2: множество B состоит из чисел и букв 1,2,6,9, b,g. Так как элементы уже перечислены, они заключаются в фигурные скобки В={1,2,6,9, b,g}.
Однако если множество бесконечно, то его элементы перечислить нельзя. Поэтому применяют второй способ.
Второй способ. Указание характеристического свойства его элементов.
Определение. Характеристическое свойство – это такое свойство, которым обладает каждый элемент, принадлежащий множеству, и не обладает ни один элемент, который ему не принадлежит.
Пример № 3. Множество А – двузначных чисел. Свойство, которым обладает любой элемент данного множества, - “быть двузначным числом”. Это характеристическое свойство дает возможность решить вопрос о том, принадлежит ли какой-либо объект множеству А или не принадлежит. Так, число 21 содержится в множестве А, поскольку оно двузначное, а число 145 множеству А не принадлежит – оно не является двузначным. Или можно использовать свойства предмета (множество квадратов можно задать как множество прямоугольников с равными сторонами и как множество ромбов с прямыми углами).
Одно и тоже множество может быть задано и первым и вторым способом.
Пример №4. Множество В натуральных чисел, меньших 7, заданное посредством указания характеристического свойства его элементов, можно задать и так: В=1,2,3,4, 5, 6, т.е. перечислив все его элементы.
3. Отношения между множествами.
Даны два множества:
Пример №1: А = a, b, c, d, e и B = b, d, k, e. Видим, что элементы b и d принадлежат одновременно множеству А и множеству В. Говорят, что b и d – общие элементы множеств А и В, а сами множества пересекаются.
Пример №2. А = 1,b, 4,6,h и B = 1,4,h,t. Элементы 1, 4 и h принадлежат двум множествам, следовательно они пересекаются.
Если множества не имеют общих элементов, то говорят, что они не пересекаются.
Пример №3 : множества А = a, b, c, d, e и В = c, d, e. Они пересекаются, и, кроме того, каждый элемент множества В является элементом множества А. В этом случае говорят, что множество В включено в А или что множество В является подмножеством множества А.
Пример №4 : множества А = a, 1, 3, е, e и В = 1, 3, e. Они пересекаются, и, кроме того, каждый элемент множества В является элементом множества А. Следовательно, множество В включено в множество А.
Определение. Множество В называется подмножеством множества А, если каждый элемент множества В является также элементом множества А.
Если В – подмножество множества А, то пишут: В А – и читают: «В – подмножество А» или «В – включается в А».
Считают, что пустое множество является подмножеством любого множества, т. е. А, и что любое множество является подмножеством самого себя, т.е. А А. Поэтому среди всех подмножеств заданного множества А должно быть обязательно пустое множество и само множество А.
Пример №5: А = 2, 3, 4. Его подмножества - одноэлементные: 2, 3, 4, двухэлементные: 2, 3, 3, 4, 2, 4, а также само множество А = 2, 3, 4 и . Таким образом, данное множество А имеет 8 подмножеств.
Пример №6: множества А = a, b, c, d, e и В = c, a, b, e, d. Они пересекаются, и каждый элемент множества А является элементом множества В, т.е. А В, и, наоборот, каждый элемент множества В является элементом множества А, т.е. В А. Следовательно, множества А и В равны.
Определение. Множества А и В называются равными, если А В и В А.
Если множества А и В равны, то пишут: А = В.
4. Операции объединения множеств и ее свойства.
Определение: Объединением двух множеств называется множество, состоящее из всех и только тех элементов, которые принадлежат хотя бы одному из множеств Х или У.
Объединение множеств обозначается символами «+» и «∪»: C=X∪Y.
Пример № 1: А={1,2,3,4} В={2,4,6} объединением {1,2,3,4,6}
Пример №2: А={2,а,6,с} В={2,5,6} объединением {2, а,5,с,6}
Пример №3: А={g,h,t,y,r} В={1,t,r} объединением {1,g,h,t,y,r}
Данную операцию можно распространить и на большее чем два число множеств. В этом случае это будет множество элементов, принадлежащих хотя бы одному из этих множеств.
Свойства объединения:
1. XUY= YUY- коммутативности
2. (X UY)UZ =XU (YUZ)=XUYUZ - ассоциативности
3. XU = X (т.е. объединение множества X и пустого множества равно множеству Х) Из свойств операций пересечения и объединения видно, что пустое множество аналогично нулю в алгебре чисел.
Существуют доказательства приведенных выше свойств
Доказательство
Формулы, подобные формулам 1-2, доказываются следующим образом. Берётся элемент, принадлежащий правой части равенства, и доказывается, что он принадлежит левой части. В результате для формулы 1, например, будет доказано, что X∪Y ⊆ Y∪X. Затем берётся элемент, принадлежащий левой части, и доказывается, что он принадлежит правой части равенства; для формулы 1 это будет означать, что Y∪X ⊆ X∪Y. Из включений X∪Y ⊆ Y∪X и Y∪X ⊆ X∪Y следует, что X∪Y = Y∪X.
Итак, пусть x ∈ X∪Y. Это значит, что либо x ∈ X, либо x ∈ Y, либо эти включения имеют место одновременно. Во всех трех случаях x ∈ Y∪X. Включение X∪Y ⊆ Y∪X доказано. Пусть теперь x ∈ Y∪X. Это значит, что либо x ∈ Y, либо x ∈ X, либо эти включения имеют место одновременно. Во всех трех случаях x ∈ X∪Y. Включение Y∪X ⊆ X∪Y доказано. Следовательно, X∪Y = Y∪X, что и требовалось доказать.
5. Операции пересечения множеств и ее свойства.
Определение: Пересечением множеств А и В называется множество, состоящее из всех тех, и только тех элементов, которые принадлежат и множеству А и множеству В.
Пример №1: А={1,2,3,4} В={2,4,6} пересечением {2,4}
Пример №2: А={g,h,t,y,r} В={1,t,r} пересечением {t, r}
Пример №3: А={2,а,6,с} В={2,5,6} пересечением {2, 6}
Пересечение множеств обозначается символами «∩» и «·» (знак умножения): С = А∩В или С = АВ.
Определение: Множества называются непересекающимися, если не имеют общих элементов, т.е. их пересечение равно пустому множеству.
Пример №4: непересекающимися множествами являются множества отличников группы и неуспевающих.
Данную операцию можно распространить и на большее чем два число множеств. В этом случае это будет множество элементов, принадлежащих одновременно всем множествам.
Свойства пересечения:
1. А∩В = В∩А - коммутативности
2. (А∩В) ∩С =А∩ (В∩С)=А∩В∩С - ассоциативности
3. А∩ =
4. А∩I = А
Доказательство
Можно выполнить графически с помощью диаграмм Эйлера-Венна или посредством последовательности утверждений. Берётся элемент, принадлежащий правой части равенства, и доказывается, что он принадлежит левой части (как вопрос 4).
6. Операции вычитания множеств и ее свойства.
Если заданы два множества, то можно не только найти их пересечение и объединение, но и вычесть из одного множества другое. Результат вычитания называют разностью и определяют следующим образом.
Определение. Разностью множеств А и В называют множество, содержащее все элементы, которые принадлежат множеству А и не принадлежат множеству В.
Разность множеств А и В обозначают А \ В. По определению: А \ В ={х/х∈А и х∉В}.
В школьном курсе математики чаще всего приходится выполнять вычитание множеств в случае, когда одно из них является подмножеством другого, при этом разность множеств А \ В называют дополнением множества В до множества А, и обозначают символом В´А, а наглядно изображают так:
Определение: Пусть В⊂ А. Дополнением множества В до множества А называется множество, содержащее все элементы множества А, которые не принадлежат множеству В.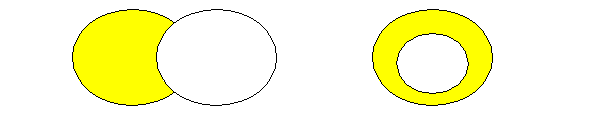
По определению: В´А ={х/х∈А и х∉В}.
Пример.
Если элементы множеств А и В перечислены и В ⊂ А, достаточно перечислить элементы, принадлежащие множеству А и не принадлежащие множеству В.
Пример №1: А = {1, 2, 3, 4, 5}, В = {2, 4}, то В´А = {1, 3, 5}.
Пример №2: А = {d,g,v,t,n}, В = {v,n}, то В´А = {d,g,t}.
В том случае, когда указаны характеристические свойства элементов множеств А и В и известно, что В ⊂ А, то множество В´А задают также с помощью характеристического свойства, общий вид которого «х∈А и х∉В».
Пример №3: А – множество четных чисел, В – множество кратных 4 чисел, то В´А - это множество, содержащее четные числа, не делящиеся на 4 – 22∈ В´А.
Вычитание– это третья операция над множествами. Условились считать, что пересечение – более «сильная» операция, чем вычитание. Что касается вычитания и объединения, то их считают равноправными.
Вычитание множеств обладает рядом свойств. В частности можно доказать, что для любых множеств А, В и С справедливы следующие равенства:
1) (А \ В) \ С = (А \ С) \ В);
2) (А∪ В) \ С = (А \ С)∪ (В \ С);
(А \ В)∩ С = (А∩ С) \ (В∩ С);
А \ (В∪ С) = (А \ В) ∩(А \ С);
А \ (В∩ С) = (А \ В) ∪(А \ С).
7. Разбиение множества на классы.
Классификацию мы выполняем достаточно часто (например, натуральные числа представляем как два класса – четные и нечетные. Углы на плоскости разбиваем на три класса: прямые, острые и тупые).
Любая классификация связана с разбиением некоторого множества объектов на подмножества. При этом считают, что множество Х разбито на классы Х₁, Х₂, …, Хn,…, если:
подмножества Х₁, Х₂, …, Хn,… попарно не пересекаются;
объединение подмножеств Х₁, Х₂, …, Хn, … совпадает с множеством Х.
Если не выполнено хотя бы одно из условий, классификацию считают неправильной.
Пример.
Если из множества Х треугольников выделить подмножества равнобедренных, равносторонних и разносторонних треугольников, то разбиения мы не получим, поскольку подмножества равнобедренных и равносторонних треугольников пересекаются (все равносторонние треугольники являются равнобедренными). В данном случае не выполнено первое условие разбиения множества на классы.
Так как разбиение множества на классы связано с выделением его подмножеств, то классификацию можно выполнять при помощи свойств элементов множеств.
Рассмотрим, например, множество натуральных чисел. Его элементы обладают различными свойствами. Положим, что нас интересуют числа, обладающие свойством «быть кратным 3». Это свойство позволяет выделить из множества натуральных чисел подмножество, состоящее из чисел, кратных 3. Тогда про остальные натуральные числа можно сказать, что они не кратны 3, т.е. получаем еще одно подмножество множества натуральных чисел. Так как выделенные подмножества не пересекаются, а их объединение совпадает с множеством натуральных чисел, то имеем разбиение этого множества на два класса.
NN
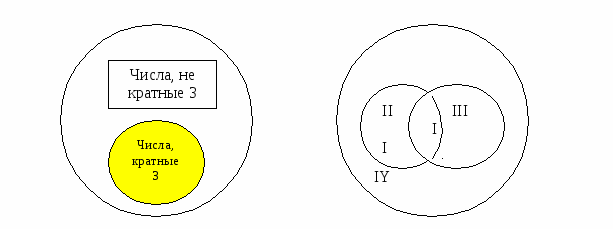
Вообще, если на множестве Х задано одно свойство, то это множество разбивается на два класса.
Первый – это класс объектов, обладающий этим свойством, а второй – дополнение первого класса до множества Х. Во втором классе содержатся такие объекты множества Х, которые заданным свойством не обладают. Такую классификацию называют дихотомической.
Рассмотрим ситуацию, когда для элементов множества заданы два свойства. Например, «быть кратным 3» и «быть кратным 5». При помощи этих свойств из множества натуральных чисел можно выделить два подмножества: А – подмножество чисел, кратных 3, и В – подмножество чисел, кратных 5. Эти множества пересекаются, но ни одно из них не является подмножеством другого. Проанализируем получившийся рисунок (справа). Конечно, разбиения множества натуральных чисел на подмножества А и В не произошло. Но круг, изображающий множество N, можно рассматривать как состоящий из четырех непересекающихся областей – на рисунке они пронумерованы. Каждая область изображает некоторое подмножество множества N. Подмножество I состоит из чисел, кратных 3 и 5; подмножество II– из чисел, кратных 3 и не кратных 5; подмножество III– из чисел, кратных 5 и не кратных 3; подмножество IY– из чисел, не кратных 3 и не кратных 5. Объединение этих четырех подмножеств есть множество N.
Таким образом, выделение двух свойств привело к разбиению множества N натуральных чисел на четыре класса.
Задание двух свойств элементов множества всегда приводит к разбиению этого множества на четыре класса.
Пример№1 при помощи двух таких свойств , как «быть кратным 3» и «быть кратным 6» множество натуральных чисел разбивается на три класса: I– класс чисел, кратных 6;II– класс чисел, кратных 3; но не кратных 6;III- класс чисел, не кратных 3.
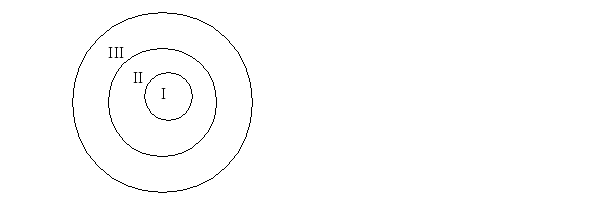
Пример №2.Множество четырехугольников  разбито на два класса:
разбито на два класса:
трапеции и прямоугольники. Данные подмножества попарно не пересекаются, а их объединения совпадают с множеством  .
.
Пример №3. Множество четырехугольников  разбито на три класса:
разбито на три класса:
квадраты, параллелограммы, прямоугольники. Так как прямоугольник и квадрат – частные случаи параллелограмма, то данные подмножества пересекаются, значит, не выполнено первое условие классификации, и разбиение множества  не получено.
не получено.
8. Объем и содержание понятия.
Всякое понятие имеет двойственную природу: с одной стороны, оно представляет собой совокупность признаков предметов, а, с другой – отражает в этих признаках саму совокупность данных предметов. Собственно, это и есть две очень важные особенности любого понятия: содержание и объем.
Определение. Содержание понятия– совокупность его существенных признаков, объём -совокупность объектов, которые имеют данные признаки.
Для того, чтобы установить содержание понятия, необходимо назвать его существенные признаки. Эти признаки могут иметь различный характер. Например, для понятия "преступление" содержание составляют признаки, выделенные законодателем в особенной части УК: противоправность, виновность, наказуемость и т.д.
Для того, чтобы установить объем понятия, необходимо установить класс объектов, включаемых в понятие. Например, объем понятия "преступление" будут составлять деяния, предусмотренные в особенной части УК: убийство, грабеж и.т.д.
Существуют две основные точки зрения на то, что включать в объем понятия: сторонники одной из них считают, что объем включает лишь элементы, существующие в настоящее время (деяния, которые в настоящее время мы можем рассматривать как таковые); сторонники другой считают, что объем включает все объекты с данными признаками, которые существовали, существуют и будут существовать (все преступления прошлого, настоящего и будущего).
Каждая из этих точек зрения имеет как достоинства, так и недостатки. К примеру, что включать в объем понятия "студент"? Ответ на этот вопрос можно дать двоякий. Если мы берем юридическое значение данного понятия (речь идет о правах и обязанностях студентов), то в объем понятия мы будем включать студентов ныне существующих. Если же берем фактическое значение термина (рассматриваем студентов как лиц, обучающихся в учреждениях профессионального образования), то это понятие будет применимо и по отношению ко всем студентам прошлого, настоящего и, видимо, будущего времени). Очевидно, наиболее правильная точка зрения будет состоять не в том, что мы априори выбираем одну из двух предложенных, а будем ориентироваться на контекст, на поставленную задачу (в нашем примере правовую или фактическую).
Для формальной логики существует приоритет объёма понятия над его содержанием. Это отражено в принципе объёмности, который при работе с понятиями предлагает отвлекаться от их содержания и оперировать только объёмами понятий. При этом появляется возможность графически изображать как понятия (их объёмы), так и отношения между понятиями (между их объёмами). Такой способ предложили Эйлер и Венн, поэтому его называют графическим способом изображения понятий или диаграммами Эйлера-Венна(вариант доказательст объединения множеств, вопрос 4).
Пример №1 отношения между понятиями «преступление» и «кража» можно изобразить в виде следующей схемы, где А – понятие «кража», а В - «преступление» (см. рис. №1).
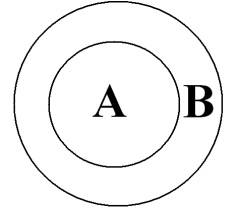
Рис. №1. Диаграмма отношений между понятиями «кража» (А) и «преступление» (В).
Другим важным положением логической теории понятий является закон обратного отношения между объёмом и содержанием понятия. Смысл этого закона можно раскрыть следующим образом: увеличение содержания понятия ведет к уменьшению его объёма и наоборот.
Пример №2 Государство, понятие, имеет определенные содержание и объём. Содержание этого понятия будет включают в себя ряд признаков: наличие определенной территории, народонаселения и пр. Объём понятия государство будут составлять все конкретные государства. Еще один признак: быть расположенным в Европе, то содержание увеличится. Вместе с тем объём данного понятия станет меньше, ведь европейских государств меньше, чем вообще государств.
Примеры №3,4
| Понятие | Объем | Содержание |
| Украинец | Общий. Все представители национальности “украинец”, которые жили, живут и будут жить | Носитель определенного и конкретного этноса, многочисленных уникальных национальных признаков (культуры, ментальности, религиозного измерения и т.д.) |
| Славянин | Общий. Все славяне и слов'янізовані народы вообще - украинцы, поляки, болгары, сербы, хорваты, русские, македонцы и т.д | Люди с определенным общим этническим прошлым (упрощенно). |
9. Определение понятий
Определения
Определить понятие – это значит дать способ, позволяющий отделить объекты, охватываемые данным понятием, от всех других объектов изучения в зависимости от присущих им существенных свойств.
Определение понятий – это логическая операция, с помощью которой указываются существенные (отличительные) свойства объекта изучения, достаточные для распознавания этого объекта, т.е. в процессе которой раскрывается содержание понятия либо устанавливается значение термина.
По способу раскрытия свойств определяемого понятия различают неявные и явные определения. К неявным определениям относятся невербальные определения, к явным –вербальные определения (лат. слово «verbalis» означает «словесный»).
Невербальные определения понятий используются в начальном курсе математики, так как младшие школьники обладают преимущественно наглядным мышлением, и именно наглядные представления о математических понятиях играют для них основную роль в обучении математике.
Невербальные определения разделяются на остенсивные(лат. слово «ostendere» – «показывать») и контекстуальные определения
Остенсивное определение– определение, в котором содержание нового понятия раскрывается путём демонстрации объектов (указания на объекты)
Пример №1.Понятия «треугольник», «круг» «квадрат», «прямоугольник» в дошкольном образовательном учреждении определяются с помощью демонстрации соответствующих моделей фигур.
Пример №2. Определение понятий «равенство» и «неравенство».
3 · 5 3 · 4 8 · 7 = 56
15 – 4
18+7 18 17 – 5 = 8 + 4
Это неравенства. Это равенства.
При ознакомлении дошкольников с новыми математическими понятиями в основном используются остенсивные определения.
Контекстуальное определение– определение, в котором содержание нового понятия раскрывается через отрывок текста, через контекст, через анализ конкретной ситуации, описывающей смысл водимого понятия.
Пример № 3.Понятия «больше», «меньше», «равно» определяются с помощью указания контекста (больше на 3 – это значит столько же и ещё 3).
Вербальное определение– перечисление существенных (отличительных) свойств данного понятия, сведенных в связное предложение.
Определение понятий можно рассматривать в виде процесса сведения одного понятия к другому, ранее изученному, и, в конечном счете, к одному из основных понятий.
Пример № 4. Квадрат это ромб, ромб – особый параллелограмм, параллелограмм – особый четырехугольник, четырехугольник – особый многоугольник, многоугольник – особая геометрическая фигура, геометрическая фигура – точечное множество.
В этой последовательности понятий каждое понятие, начиная со второго, является родовым понятием для предыдущего понятия, т.е. объёмы этих понятий находятся между собой в последовательном отношении включения:
Va VвVcVd VeVfVq, где а:«квадрат»,в:«ромб»,
с:«параллелограмм»,d:«четырехугольник»,e:«многоугольник»,
f:«геометрическая фигура», q:«точечное множество»
Например, определение понятия «квадрат».
«Квадратом называется прямоугольник, у которого все стороны равны».
Сначала указано определяемое понятие - «квадрат», а затем приведено определяющее понятие, в котором можно выделить две части: 1) понятие «прямоугольник», которое является родовым по отношению к понятию «квадрат»; 2) свойство «иметь все равные стороны», которое позволяет выделить из всевозможных прямоугольников один вид – квадрат, поэтому это свойство называют видовым отличием.
Пример № 5. Параллелограммом называется четырехугольник, у которого противоположные стороны параллельны. Сначала указано определяемое понятие «параллелограмм», потом определяющее понятие , где понятие – четырехугольник- является родовым к параллелограмму, свойство – противоположные стороны параллельны- видовое свойство.
Видовым отличием называются свойства (одно или несколько), которые позволяют выделить определяемое понятие из объема родового понятия.
Структура определений через род и видовое отличие
Определяемое понятие=Родовое понятие+Видовое отличие
Способы определения понятий являются частными случаями определения через род и видовое отличие.
Генетическое или конструктивное определение, т.е. определение, в котором видовое отличие определяемого понятия указывает на его происхождение или способ образования, построения (греч. слово «denesis» –«происхождение», лат. слово «constructio» –«построение»).
Например.
1. Определение понятия «угол».
«Углом называется фигура, образованная двумя углами, исходящими из одной точки». В этом примере понятие «фигура» является родовым, а способ образования этой фигуры – «образована двумя лучами, исходящими из одной точки» - является видовым отличием.
Индуктивное определениеили определение понятия с использованием формулы, позволяющей сформулировать общее отличительное свойство данного понятия (лат. слово «inductio» – «наведение» на рассуждение от частного к общему).
Например, определение понятия «функция прямой пропорциональности».
«Функцией прямой пропорциональности называется функция вида «y=kx, гдеxR,k≠0». В этом примере понятие «функция» - родовое понятие, а формула «y=kx, гдеxR,k≠0» - видовое отличие понятия «функция прямой пропорциональности» от других видов функций.
10. Математические предложения: высказывания и высказывательные формы.
Определение. Высказыванием в математике называют предложение, относительно которого имеет смысл вопрос: истинно оно или ложно.
Пример №1, Высказывание «Число 6 делится на 2, и число 6 делится на 3» - истинно, а высказывание «Число 6 делится на 2, и число 6 больше 10» - ложно.
Пример №2, Высказывание «Число 6 делится на 2 или число 6 больше 10» - истинно, а высказывание «Число 6 делится на 5 или число 6 больше 10» - ложно.
Пример №2. «3 – простое число» является высказыванием, поскольку оно истинно.
Высказывания принято обозначать прописными буквами латинского алфавита: А, В, С, …, Z. Если высказывание А истинно, то записывают: А – «и», если же высказывание А – ложно, то пишут: А – «л».
«Истина» и «ложь» называются значениями истинности высказывания. Каждое высказывание либо истинно, либо ложно, быть одновременно тем и другим оно не может.
Предложение х+4=8 называется высказывательной формой, то есть оно порождает множество высказываний одной и той же формы.
Различают одноместные, двухместные и т.д. высказывательные формы и обозначают: А(х), А(х,у) и т.д. Например, х+5=8 – одноместная высказывательная форма, а предложение «Прямая х параллельна прямой у» – двухместная.
В высказывательной форме переменные могут содержаться неявно. Например, в предложениях: «число четное», «две прямые пересекаются» переменных нет, но они подразумеваются: «Число х – четное», «Две прямые х и у пересекаются».
Определение. Одноместной высказывательной формой, заданной на множестве Х, называется предложение с переменной, которое обращается в высказывание при подстановке в него значений переменной из множества Х.
Множество таких значений переменных называют множеством истинности высказывательной формы.
Например, множество истинности высказывательной формы х5, заданной на множестве действительных чисел, будет промежуток (5;). Множество истинности высказывательной формы х+5=8, заданной на множестве целых неотрицательных чисел, состоит из одного числа 3.
Слова «и», «или», «если …, то…», «тогда и только тогда, когда», а также частицу «не» (слова «неверно, что») называются логическими связками. Предложения, образованные из других предложений с помощью логических связок, называют составными. Предложения, не являющиеся составными, называют элементарными.
Примеры составных предложений:
1) Число 28 четное и делится на 7.
2) Число х меньше или равно 8.
3) число 14 не делится на 4.
Все три предложения, являясь с логической точки зрения составными, по своей грамматической структуре – простые. Не всегда, но так бывает: простое предложение по своей логической структуре может быть составным.
Чтобы определить значение истинности составного высказывания, надо знать смысл логических связок, с помощью которых оно образовано из элементарных, и уметь выявлять логическую структуру высказывания.
Для выявления логической структуры составного предложения нужно установить:
-из каких элементарных предложений образованно данное составное предложение;
-с помощью каких логических связок оно образовано.
«Если углы вертикальные, то они равны». Оно состоит из двух элементарных предложений: предложения А – «углы вертикальные» и предложения В - «углы равны». Соединены они в одно составное предложение с помощью логической связки «если …, то…». Говорят, что данное составное предложение имеет логическую структуру (форму): «если А, то В».
11 Кванторы общности и существования.
Определение. Квантором называют символ математической логики, указывающий на определенную логическую операцию, которую необходимо осуществить, чтобы дать количественную характеристику некоторой области объектов. Квантор показывает, о скольких объектах (элементах) говорится в том или ином высказывании.
Различают два основных вида кванторов: квантор общности и квантор существования. Под квантором общности понимаются слова: «любой», «каждый», «всякий», «все», а под квантором существования подразумеваются слова и обороты: «существует», «найдется хотя бы один», «есть», «имеется».
Пример № 1.Пусть Р(х) – высказывательная форма (предикат), заданная на множестве Х. Поставив перед ней квантор общности, получим высказывание: «Для всех хХ выполняется высказывательная форма Р(х)», которое записывается в символах:(xX) P(x).
Символ – это перевернутая первая буква английского слова «All» - «все».
Пример №2. Р(х) – «Простое число х нечетно»
Добавим квантор общности  – «Всякое простое число х нечетно» - ложное высказывание.
– «Всякое простое число х нечетно» - ложное высказывание.
Под выражением  понимают высказывание истинное, когда Р(х) истинно для каждого элемента х из множества М и ложное в противном случае. Это высказывание уже не зависит от х.
понимают высказывание истинное, когда Р(х) истинно для каждого элемента х из множества М и ложное в противном случае. Это высказывание уже не зависит от х.
Пример № 3.Высказывание, содержащее квантор общности, истинно в том и только в том случае, если для всех элементов х из множества Х выполняется высказывательная форма Р(х); если же хотя бы для одного элементах из множества Х высказывательная форма Р(х)не выполняется, то высказывание с квантором общности будет ложно.
Пример № 4. Пусть P(x) -предикат определенный на множестве М. Под выражением  понимают высказывание, которое является истинным, если существует элемент
понимают высказывание, которое является истинным, если существует элемент  , для которого P(x) истинно, и ложным – в противном случае. Это высказывание уже не зависит от x. Соответствующее ему словесное выражение звучит так: “Существует x, при котором P(x) истинно.” Символ
, для которого P(x) истинно, и ложным – в противном случае. Это высказывание уже не зависит от x. Соответствующее ему словесное выражение звучит так: “Существует x, при котором P(x) истинно.” Символ  называют квантором существования. В высказывании
называют квантором существования. В высказывании  переменная x связана этим квантором (на нее навешен квантор).
переменная x связана этим квантором (на нее навешен квантор).
 ( Читают: «Существует такое х из М, при котором Р от х истинно»)
( Читают: «Существует такое х из М, при котором Р от х истинно»)
Под выражением  понимают высказывание, которое является истинным, если существует элемент х€М (хотя бы один), для которого Р(х) истинно, и ложным в противном случае.
понимают высказывание, которое является истинным, если существует элемент х€М (хотя бы один), для которого Р(х) истинно, и ложным в противном случае.
Пример №5 : Р(х) «Число х кратно 5»
 -любое натуральное число кратно 5»
-любое натуральное число кратно 5»
каждое натуральное число кратно 5» ложные высказывания
-все натуральные числа кратны 5»
 - существует натуральное число кратно 5
- существует натуральное число кратно 5
- найдется натуральное число кратно 5 истинные высказывания
- хотя бы одно натуральное число кратно 5
Пример № 6. Пусть на множестве N натуральных чисел задана высказывательная форма Р(х): «Число х больше 5». Используя кванторы, из высказывательной формы можно получить, например, следующие высказывания: 1) «Любое натуральное число х больше 5»; 2) «Каждое натуральное число х больше 5»; 3) «Существует натуральное число х, большее 5»; 4) «Найдется натуральное число х, большее 5».
12. Высказывания с кванторами.
1. Пусть на множестве N задана высказывательная форма А(х): «Число х кратно 3». Поставим перед высказывательной формой слово «всякое». Получим ложное высказывание: «Всякое число х кратно 3» (хN). Поставив перед данной высказывательной формой слово «существует», получим истинное высказывание: «Существует число х, кратное 3» (хN).
2. Рассмотрим числа: 1, 2, 3, 4, 5. Про них можно сказать: «Все числа однозначные. Некоторые из данных чисел чётные».
Относительно этих предложений имеет смысл вопрос, истинны они или ложны, следовательно эти предложения – высказывания.
Итак, высказывательную форму (предикат) можно превратить в высказывание, поставив перед формой особые слова, которые называются в логике кванторами.
Квантором называют символ математической логики, указывающий на определенную логическую операцию, которую необходимо осуществить, чтобы дать количественную характеристику некоторой области объектов.
Таким образом, квантор показывает, о скольких объектах (элементах) говорится в том или ином высказывании.
Различают два основных вида кванторов: квантор общности и квантор существования.
Еще примеры
Истинность высказываний с квантором общности устанавливается путем доказательства. Чтобы убедиться в ложности достаточно привести контрпример.
Пример:
Задание ребенку: «Назови одним словом».


| Вариант ответа | Математическое предложение | Установка истинности |
| «Фигуры» | «Все предметы являются фигурами» | «И»,т.к. квадрат – фигура, треугольник – фигура, прямоугольник – фигура, круг – фигура. (доказа-тельство) |
| «Многоуголь-ники» | «Все предметы являются многоугольниками» | «Л»,т.к. круг не является многоугольником. (контрпример) |
Истинность высказывания с квантором существования устанавливается при помощи конкретного примера. Чтобы убедиться в ложности, необходимо провести доказательство.
Пример:
Наглядный материал: Игрушки в коробке.
Вопрос ребенку: «Есть ли в коробке мячи?»
Математическое предложение: «Хотя бы один из предметов – мяч».
| Вариант ответа | Установление значение истинности |
| Да | Показ хотя бы одного мяча (конкретный пример). |
| нет | Просмотр каждой игрушки (доказательство). |
Операция получения высказываний из высказывательных форм (предикатов) с помощью кванторов называется операцией навешивания кванторов.
13. Взаимно-однозначные соответствия. Равномощные множества
Определение. Взаимно однозначным соответствием между множествами Х и У называется такое соответствие, при котором каждому элементу множества Х сопоставляется единственный элемент множества У и каждый элемент множества У соответствует только одному элементу множества Х.
Пример
Пример № 1. Пусть Х – множество действительных чисел, У – множество точек координатной прямой. Соответствие между ними таково: действительному числу сопоставляется точка координатной прямой. Это соответствие взаимно однозначное, так как каждому действительному числу сопоставляется единственная точка координатной прямой и каждая точка на прямой соответствует только одному числу.
Пример №2. Пусть Х – множество кругов, У – множество квадратов и соответствие между ними задано при помощи стрелок.
Это соответствие взаимно однозначное, так как каждому кружку из множества Х сопоставляется единственный квадрат из множества У и каждый квадрат из У соответствует только одному кружку из множества Х.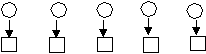
В математике взаимно однозначное соответствие между множествами Х и У часто называют взаимно однозначным отображением множества Х на множество У.
Определение. Множества Х и У называются равномощными, если между ними можно установить взаимно однозначное соответствие.
Если множества Х и У равномощны, то пишут Х У.
Равномощными могут быть как конечные, так и бесконечные множества. Равномощные конечные множества называют еще равночисленными. В начальном обучении математике равночисленность выражается словами «столько же» и может использоваться при ознакомлении учащихся со многими понятиями. Например, чтобы ввести равенство чисел, сравнивают два множества, устанавливая между их элементами взаимно однозначное соответствие ( пишут, что 5 = 5, так как кружков столько же, сколько квадратов).
Понятие равночисленности множеств лежит и в основе определения отношений «больше на …» и «меньше на…» . Например, чтобы утверждать, что 6 больше 4 на 2, сравнивают два множества, устанавливая взаимно однозначное соответствие между множеством Х, в котором 4 элемента, и подмножеством У1другого множества У, в котором 6 элементов, и делают вывод: треугольников столько же, сколько кружков, и еще 2. Другими словами, треугольников на 2 больше, чем кружков.
В математике доказано, что для бесконечного множества А всегда найдется такое его подмножество В, что между А и В можно установить взаимно однозначное соответствие. Иногда это утверждение считают определением бесконечного множества.
Определение. Если бесконечное множество равномощно множеству N натуральных чисел, его считают счетным.
Любое бесконечное подмножество множества N счетно: чтобы пронумеровать его элементы, надо расположить элементы подмножества в порядке возрастание и нумеровать один за другим. Так, счетно множество всех нечетных натуральных чисел, множество натуральных чисел, кратных 5 и др. Счетными являются также множества всех целых чисел, всех рациональных.
Примеры.
Пусть Х – множество точек отрезка АВ, У – множество точек отрезка СD, причем длины отрезков различны. Так как между данными множествами можно установить взаимно однозначное соответствие, то множества точек АВ и СD равномощны.
Пусть даны два множества X= {а, b, с, d} иY= {k, l, m, n}.
Heпересчитывая число их элементов, а лишь установив взаимно однозначное соответствие, можно сказать, что множество Y содержит элементов столько же, сколько и множество X. Говорят, что множества X и Y имеют одинаковую мощность, или они равномощны.
14. Понятие отношения между элементами одного множества.
Определение. Отношением между элементами множества Х или отношением на множестве Х называется всякое подмножество декартова произведения ХХ.
Чтобы определить общее понятие отношения на множестве, рассмотрим сначала конкретный пример.
Пример № 1. Пусть на множестве Х = 2, 4, 6, 8 задано отношение «меньше». Это означает, что для любых двух чисел из множества Х можно сказать, какое из них меньше: 2 4, 2 6, 2 8, 4 6, 4 8, 6 8. Но все эти пары есть элементы декартова произведения ХХ, поэтому об отношении «меньше», заданном на множестве Х, можно сказать, что оно является подмножеством множества ХХ.
Определение. Бинарным отношением на множестве Х называется всякое подмножество декартова произведения ХХ.
Пример № 2. Если R – отношения на множестве Х, то, согласно определению, R ХХ. С другой стороны, если задано некоторое подмножество множества ХХ , то оно определяет на множестве Х некоторое отношение R.
Примеры бинарных отношений.
на множестве целых чисел Z отношения «делится», «делит», «равно», «больше», «меньше», «взаимно просты»;
на множестве прямых пространства отношения «параллельны», «взаимно перпендикулярны», «скрещиваются», «пересекаются», «совпадают»;
на множестве окружностей плоскости «пересекаются», «касаются», «концентричны».
Замечание. Утверждение о том, что элементы х и у находятся в отношении R, можно записать так: (х,у) R или х R у. Последняя запись читается : “Элемент х находится в отношении R с элементом у”.
15. Способы задания отношений
По определению отношения R между элементами множества Х есть всякое подмножество декартова произведения Х Х, т.е. множество, элементами которого являются упорядоченные пары. Поэтому способы задания отношений, по существу, такие же, как и способы задания множеств.
Отношение R на множестве Х можно задать, перечислив все пары элементов, взятых из множества Х и связанных этим отношением.
Формы записи при этом могут быть различными. Например, некоторое отношение R на множестве Х = 4, 5, 6, 7, 9можно задать, записав множество пар: (5,4),(6,4),(6,5),(7,4),(7,5),(7,6),(9, 4),(9,5),(9,6),(9,7).То же отношение можно задать при помощи графа.
Отношения на конечном множестве Х можно представлять наглядно, при помощи особых чертежей, состоящих из точек, соединенных стрелками. Такие чертежи называют графами.
Построим граф отношения «меньше», заданного на множестве Х = 2, 4, 6, 8. Для этого элементы множества Х изобразим точками (их называют вершинами графа), а отношение «меньше» – стрелкой.
2• •4
8 6
Пример № 1.
На множестве Х другое отношение – «кратно». Граф этого отношения будет в каждой вершине иметь петлю (стрелку, начало и конец которой совпадают), так как каждое число кратно самому себе.
2 4







8 6

Пример №2.
Пусть заданы рассмотренные выше отношения «меньше» и «кратно», форма предложений - «число х меньше числа у» и «число х кратно числу у». Отношения «меньше» и «кратно» можно записать в таком виде: «х у», «ху». Отношение «х больше у на 3» можно записать в виде равенства х = у + 3 (или х – у = 3). Отношение между прямыми плоскости задают, используя символы: х // у, х у.
Для отношения R, заданного на множестве Х, всегда можно задать отношение R -1, ему обратное. Пример № 3.
Если R – отношение “х меньше у”, то обратным ему будет отношение “ у меньше х”.
Пример № 4.
Если R – отношение “х больше у”, то обратным ему будет отношение “ у больше х”.
Понятием отношения, обратного данному, часто пользуются при начальном обучении математике.
Например, чтобы предупредить ошибку в выборе действия, с помощью которого решается задача: «У Пети 7 карандашей, что на 2 меньше, чем у Бори. Сколько карандашей у Бори?» – ее переформулируют: «У Пети 7 карандашей, а у Бори на 2 больше. Сколько карандашей у Бори?». Видим, что переформулировка свелась к замене отношения «меньше на 2» обратным ему отношением «больше на 2».
Пример № 5.
У Маши 5 конфет, что вдвое больше, чем у Кати. Переформулировка- У Маши 5 конфет, а у Кати в 2 раза меньше.
Пример № 6.
На лужайке растет 10 цветов, что на 5 меньше, чем на поле. Переформулировка – На лужайке растет 10 цветов, а на поле на 5 цветов больше.
16. Свойства отношений.
Отношение, заданное на множестве, может обладать рядом свойств, а именно:
1. Рефлексивность
Определение. Отношение R на множестве Х называется рефлексивным, если каждый элемент х множества Х находится в отношении R с самим собой.
Используя символы, это отношение можно записать в таком виде:
R рефлексивно на Х Û("х Î Х) х R х
Пример. Отношение равенства на множестве отрезков рефлексивно, т.к. каждый отрезок равен себе самому.
Примерами рефлексивных отношений являются и отношение «кратно» на множестве натуральных чисел (каждое число кратно самому себе), и отношение подобия треугольников (каждый треугольник подобен самому себе), и отношение «равенства» (каждое число равно самому себе) и др.
2. Антирефлексивность
Определение. Отношение R на множестве Х называется антирефлексивным, если ни один элемент х множества Х не находится в отношении R с самим собой.
R антирефлексивно на Х Û("х Î Х) 
Пример. Отношение «прямая х перпендикулярна прямой у» на множестве прямых плоскости антирефлексивно, т.к. ни одна прямая плоскости не перпендикулярна самой себе.
Граф антирефлексивного отношения не содержит ни одной петли.
Существуют отношения, не являющиеся ни рефлексивными, ни антирефлексивными. Например, рассмотрим отношение «точка х симметрична точкеу» на множестве точек плоскости.
· у
 l
l
х
Точка х симметрична точке х – истинно; точка у симметрична точке у – ложно, следовательно, мы не можем утверждать, что все точки плоскости симметричны сами себе, также мы не можем и утверждать, что ни одна точка плоскости не симметрична сама себе.
3. Симметричность
Определение. Отношение R на множестве Х называется симметричным, если из того, что элемент х находится в отношении R с элементом у, следует, что и элемент у находится в отношении R с элементом х.
R симметричнона Х Û("х, у Î Х) х R у Þ у R х
Пример. Отношение «прямая х пересекает прямую у на множестве прямых плоскости» симметрично, т.к. если прямая х пересекает прямую у, то и прямая уобязательно будет пересекать прямую х.
Примерами симметричных отношений могут быть следующие: отношение «параллельности» отрезков, отношение «перпендикулярности» отрезков, отношение «равенства» отрезков, отношение подобия треугольников, отношение «равенства» дробей и др.
4. Асимметричность
Определение. Отношение R на множестве Х называется асимметричным, если ни для каких элементов х, у из множества Х не может случиться, что элемент х находится в отношении R с элементом у и элемент у находится в отношении R с элементом х.
R асимметричнона Х Û("х, у Î Х) х R у Þ 
Пример. Отношение «х
Граф асимметричного отношения не имеет петель и если две вершины графа соединены стрелкой, то эта стрелка только одна.
Отношение «больше» для чисел (если х больше у, то у не может быть больше х), отношение «больше на» и др.
5. Антисимметричность
Определение. Отношение R намножестве Х называется антисимметричным, если из того что х находится в отношении с у, а у находится в отношении с х следует, что х = у.
R антисимметрично на Х Û("х, у Î Х) х R у Ù у R х Þ х = у
Пример. Отношение «х £ у» антисимметрично, т.к. условия х £ у и у £ х одновременно выполняются только тогда, когда х = у.
Граф антисимметричного отношения имеет петли и если две вершины графа соединены стрелкой, то эта стрелка только одна.
6. Транзитивность
Определение. Отношение R намножестве Х называется транзитивным, если для любых элементов х, у, z из множества Х из того, что х находится в отношении с у, а унаходится в отношении с z следует, что х находится в отношении с z.
R транзитивнона Х Û("х, у, z Î Х) х R у Ù у R z Þ х R z
Пример. Отношение «х кратно у» транзитивно, т.к. если первое число кратно второму, а второе кратно третьему, то первое число будет кратно третьему.
Граф транзитивного отношения с каждой парой стрелок от х к у и от у к z содержит стрелку, идущую от х к z.
7. Связность
Определение. Отношение R на множестве Х называется связным, если для любых элементов х, у из множества Х х находится в отношении с у или у находится в отношении с х или х = у.
R связнона Х Û("х, у, z Î Х) х R у Ú у R z Ú х = у
Другими словами: отношение R намножестве Х называется связным, если для любых различных элементов х, у из множества Х х находится в отношении с у или унаходится в отношении с х или х = у.
Пример. Отношение «х
На графе связного отношения все вершины соединены между собой стрелками.
Пример. Проверить, какими свойствами обладает
отношение «х – делитель у», заданное на множестве
Х = {2; 3; 4; 6; 8}.
Построим граф данного отношения:
1) данное отношение рефлексивно, т.к. каждое число из данного множества является делителем самого себя;
2) свойством антирефлексивности данное отношение не обладает;
3) свойство симметричности не выполняется, т.к. например, 2 является делителем числа 4, но 4 делителем числа 2 не является;
4) данное отношение антисимметрично: два числа могут быть одновременно делителями друг друга только в том случае, если эти числа равны;
5) отношение транзитивно, т.к. если одно число является делителем второго, а второе – делителем третьего, то первое число обязательно будет делителем третьего;
6) отношение свойством связности не обладает, т.к. например, числа 2 и 3 на графе стрелкой не соединены, т.к. два различных числа 2 и 3 делителями друг друга не являются.
Таким образом, данное отношение обладает свойствами рефлексивности, асимметричности и транзитивности.