Типичные ошибки на ОГЭ по математике

Шарова Людмила Владимировна,

учитель математики

МБОУ «Ашковская основная школа»

Типичные ошибки на ОГЭ

по математике

Рассмотрим ошибки учащихся, которые наиболее часто допускаются на ОГЭ по математике.

Итоговая аттестация – первая серьёзная проверка освоения основной образовательной программы основного общего образования. Результаты, полученные выпускниками на ГИА – это и результат освоения ими школьной программы, и оценка работы учителя.

Специфика математики как школьного предмета состоит в том, что ее изучение в значительной степени строится на системе опорных знаний, без овладения которыми невозможно дальнейшее продвижение по курсу. В ходе ОГЭ учащийся должен продемонстрировать наличие у него опорных знаний, позволяющих изучать математику в старшей школе.

ОГЭ проверяет не только знания по предмету, но и умение читать и понимать прочитанное, внимательность и аккуратность в оформлении решений (запись ответов в бланк), умение проверять свои решения.

Можно утверждать, что полученные учащимися баллы в большинстве случаев могли бы быть значительно выше. Это возможно в случае, если школьники более критично отнеслись бы как к приводимым ими ответам, так и к заполнению бланков и записи решения задач с развернутым ответом.

Ошибки, которые допускают обучающиеся в 1 части экзаменационной работы, можно условно делить на три группы: технические, содержательные, связанные с невнимательным чтением условия задачи.

Технические ошибки – это, во-первых, неграмотное заполнение бланка с кратким ответом.

Рассмотрим примеры:

1) К заданиям, где требуется установить соответствие, а это соответствие в КИМах предлагается привести в форме таблицы, учащиеся нередко переносят в бланк ответов как «А2Б4В3», или «2,4,3», или «2;4;3», или «2 4 3» вместо верного «243».

2) Запятую или точку с запятой ученики также часто приводят и в ответах к заданиям, где требуется указать номера верных (неверных) утверждений, в то время как имеется указание на то, что ответом к этим заданиям является последовательность цифр, записанных в любом порядке без пробелов и использования других символов.

3) Нередко ученики в бланк ответов вписывают единицы измерения, что нельзя делать, – если единицы длины, веса и т.п. еще можно верифицировать вручную, то знак градусов компьютер может принять и за ноль.

4) Случается, что задача учащимся решена неверно и в неверном ответе содержится знак радикала – в этом случае следовало бы пересмотреть решение, но школьники упорно пытаются вписать знак арифметического квадратного корня в клетки бланка ответов.

5) В некоторых работах встречается, что числа написаны небрежно, иногда бывает невозможно понять, что написано 6 или 0, 5 или 6, 1 или 7, 3 или 9.

Содержательные ошибки.

Все задания, которые имеют жизненные формулировки, имеют реальные числовые данные, поэтому следует сопоставлять ответ с реальной ситуацией, делать проверку, прикидку результата. Это относится и к «чисто математическим» задачам. Между тем, можно нередко встретить неверные ответы, для которых даже грубая прикидка говорит об их ошибочности.

Покажем это на нескольких примерах:

В задаче требуется найти высоту равностороннего треугольника со стороной 54√3. Приводимые иногда ответы «9» или «162» значительно меньше или больше верного – для исключения таких ответов достаточно попробовать привести геометрическую конструкцию с данными, которые известны в условии и получены в ответе.

Дана задача: «Найдите корень уравнения 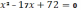 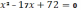. Если уравнение имеет более одного корня, укажите меньший из них». Число 9, являющееся большим корнем данного уравнения, представляется ошибочно записанным в ответ, но все другие числа, отличные от меньшего второго корня 8 (а их нередко, причем различные, и указывают в ответе), не проходят элементарную проверку подстановкой.

Дано задание: «27 выпускников школы собираются учиться в технических вузах. Они составляют 30% от числа выпускников. Сколько в школе выпускников?». Встречаются работы, в которых ответом к данной задаче указывалось число 8,1, что явно противоречит здравому смыслу.

Следующая группа ошибок в заданиях с кратким ответом связана с невнимательным чтением условия задачи.

Вот некоторые примеры:

В одном задании требовалось полученный ответ округлить до целого числа, чего не сделали некоторые учащиеся, записывая верный точный ответ с дробной его частью.

В задании требовалось указать номер первого отрицательного члена заданной последовательности. Видится, что приводимый иногда ответ «–3» явно не есть номер члена прогрессии, а сам этот член заданной прогрессии.

В задании на чтение графиков требовалось по заданной диаграмме указать число стран, в которых средний балл тестирования отличается от среднего балла российских участников не меньше, чем на 15. Учащиеся представляют ошибочный ответ - перечисляют названия стран, а не их количество.

Анализ выполнения заданий с развернутым ответом показывает, что одной из самых больших проблем выпускников 9 класса является прочтение условия задачи и его содержательная интерпретация на математический язык.

Задание № 20 – Алгебраические выражения, уравнения, неравенства и их системы.

Типичные ошибки:

- потеря корня;

- неправильно сформированный ответ;

- к нулю или между собой приравнены два абсолютно разных по значению выражения;

- содержательные ошибки, наличие которых не позволяло засчитать это задание;

- логически незавершенные решения при полученном верном ответе, что свидетельствует о несформированном навыке логически верно записывать интуитивно понятное решение;

- вычислительные ошибки.

Задание № 21 - Текстовая задача.

Типичные ошибки:

- перевод содержания задачи на математический язык;

- составление уравнений, связывающих данные величины и переменные, которые вводит учащийся;

- вычислительные ошибки при решении уравнения;

- наличие неправильно сформированного ответа в части отсутствия именованных величин.

Задание № 22 – Функции и их свойства. Графики функций.

Типичные ошибки:

- неправильно построен график;

- записано верное значение параметра, но не указано, как оно получено;

- отсутствуют единичный отрезок на координатных осях, направления координатных осей.

Задание № 23 - Уметь выполнять действия с геометрическими фигурами. Проводить доказательные рассуждения при решении задач.

Типичные ошибки:

- неверное построение чертежа к задаче;

- решают частную задачу, изменяя фактически ее смысл;

- неправильно указан признак подобия треугольников;

- неверно найдены сходственные стороны;

- неверно решена пропорция;

- вычислительные ошибки.

Задание № 24 - Проводить доказательные рассуждения при решении задач.

Типичные ошибки:

- неверное построение чертежа к задаче

- неполное доказательство;

- интуитивно понятные факты не доказывают, считая их очевидными, а также не умеют математически грамотно и ясно записывать решение, приводя при этом необходимые пояснения и обоснования.

Задание № 25 - Уметь выполнять действия с геометрическими фигурами. Решать планиметрические задачи на нахождение геометрических величин. Различать взаимное расположение геометрических фигур на плоскости, изображать геометрические фигуры; выполнять чертежи по условию задачи. Проводить доказательные рассуждения при решении задач.

Типичные ошибки:

-доказательство верное, но записи неаккуратные, иногда просто невозможно понять, что написано учеником;

- присутствуют только отдельные факты, по сути, не связанные с тем, что необходимо доказать;

- неправильно понимают условие задания;

- использовали неверные методы решения.

Выводы:

Основные проблемы, возникающие при написании выпускниками экзаменационной работы:

• неумение понять суть вопроса, содержание задания, приводящее к построению неверного хода решения;

• недостаточно развитые умения смыслового чтения, не позволяющие построить адекватную математическую модель по условию задания;

• вычислительные навыки слабо сформированы;

• неспособность грамотно сформулировать решение в письменном виде, небрежное оформлении письменного решения задачи;

• недостаточные геометрические знания, слабая графическая культура;

• неумение проводить анализ условия задания при решении практических и ситуационных задач, неумение применять известный алгоритм в нестандартной ситуации;

• недостаточно развиты аналитические навыки.

Пути преодоления:

1. Рабочая программа должна не только эффективно использовать учебное время при изучении текущего материала, организации повторения и подготовки выпускников к итоговой аттестации, но и составлять часть целостной системы, позволяющей учитывать освоение проблемных тем в каждом классе, а также ликвидировать пробелы в знаниях и умениях учащихся.

2. Необходимо проводить диагностические работы, направленные на выявление уровня подготовки учащихся по отдельным темам, что позволит спланировать индивидуальную и групповую работу обучающихся.

3. При изучении нового материала и его отработке необходимо сочетать различные методы обучения: традиционные и интерактивные, направленные на организацию самостоятельной работы каждого ученика, что также позволит устранить пробелы в знаниях и умениях, и поможет проводить подготовку к аттестации дифференцированно для слабых и сильных учеников.

4. Особое внимание следует уделять формированию навыков самоконтроля и самопроверки выполненных заданий.

5. Необходимо повышать уровень вычислительных навыков, развивать умение пользоваться справочными материалами, читать условие и вопрос задачи, записывать математически верно решение задачи, применять знания в нестандартных ситуациях.

6. Со слабоуспевающими школьниками необходимо выделить круг доступных ему заданий, помочь освоить основные математические факты, позволяющие их решать и сформировать уверенные навыки их решения. Для «средних» учеников необходимо использовать методику, при которой они смогут перейти от теоретических знаний к практическим навыкам, от решения стандартных алгоритмических задач к решению задач похожего содержания, но иной формулировки и применению уже отработанных навыков в новой ситуации. Для сильных учеников требуется создание условия для продвижения: дифференцированные по уровню сложности задания, возможность саморазвития, помощь в решении заданий второй части.

7. «Нарешивание» заданий Открытого банка ОГЭ необходимо для формирования устойчивых навыков решения, но его нужно сочетать с фундаментальной подготовкой, позволяющей сформировать у учащихся общие учебные действия, способствующие более эффективному усвоению изучаемых вопросов, а также дифференциации обучающихся по уровню подготовки.

8. В процессе подготовки к ОГЭ должны участвовать все стороны: дети, школа и родители, поэтому необходимо своевременно знакомить родителей с нормативными документами по подготовке к экзаменам, информировать их о процедуре итоговой аттестации, о всевозможных методических рекомендациях и ресурсах, о результатах пробных испытаний и текущей успеваемости.

4