Трапеция. теорема Фалеса.

Трапеция

Теорема Фалеса

К учебнику Л.С.Атанасяна

Геометрия 7 - 9, Глава V, п. 45, 8 класс

Автор: Софронова Наталия Андреевна,

учитель математики высшей категории

МОУ «Упшинская основная общеобразовательная школа»

Оршанского района Республики Марий Эл

трапеции

Четырехугольник, у которого две стороны параллельны, а две другие стороны не параллельны, называется трапецией

Каким общим свойством обладают данные четырехугольники?

Боковая сторона

Боковая сторона

Четырехугольник АВСD – трапеция (ВС ǁ АD )

В

С

Основание

D

А

Основание

Параллельные стороны трапеции называются её основаниями, а две другие – боковыми сторонами

Боковая сторона

Боковая сторона

ǁ

ǁ

Средняя линия трапеции

В

Основание

С

N

Средняя линия

M

D

А

Основание

Отрезок, соединяющий середины боковых сторон трапеции, называется её средней линией

ǁ

ǁ

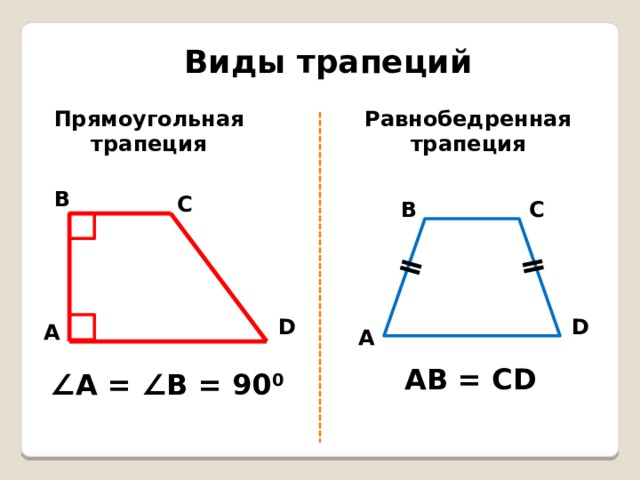
Виды трапеций

Прямоугольная

Равнобедренная

трапеция

трапеция

В

С

В

С

D

D

А

А

АВ = СD

∠ А = ∠В = 90 0

ǁ

ǁ

∟

∟

Свойства равнобедренной трапеции

В

С

BN⏊AD

CM⏊AD

BN = CM

А

D

ǁ

ǁ

N

M

∠ A = ∠D

AN = DM

Δ ABN = Δ DCM

ǁ

ǁ

Свойства равнобедренной трапеции

С

В

∠ A = ∠D

∠ A + ∠B = 180 0

∠ D + ∠C = 180 0

∠ B = ∠C

А

D

В равнобедренной трапеции углы при основании равны

ǁ

ǁ

Свойства равнобедренной трапеции

С

В

ΔABC = ΔDCB

AC = DB

D

А

В равнобедренной трапеции диагонали равны

ǁ

ǁ

Свойства равнобедренной трапеции

∠ A = ∠D

∠ B = ∠C

С

В

AC = DB

А

D

В равнобедренной трапеции:

углы при основании равны ,

диагонали равны

∟

∟

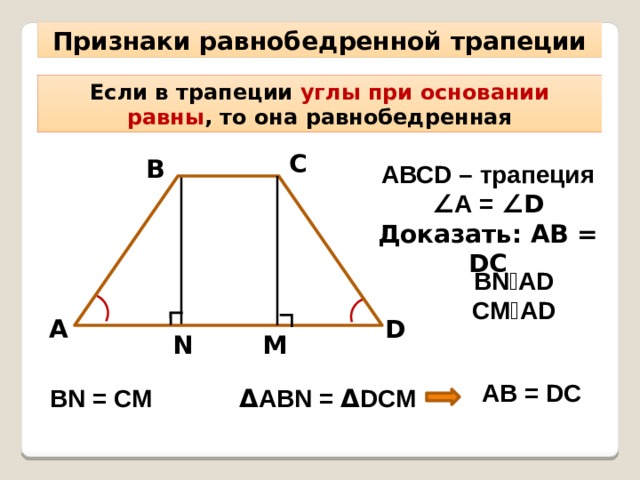
Признаки равнобедренной трапеции

Если в трапеции углы при основании равны , то она равнобедренная

С

В

АВСD – трапеция

∠ А = ∠D

Доказать: АВ = DC

BN⏊AD

CM⏊AD

D

А

M

N

AB = DC

BN = CM

Δ ABN = Δ DCM

ǁ

ǁ

ǁ

Если в трапеции углы при основании равны , то она равнобедренная

С

2-й способ

В

АВСD – трапеция

∠ А = ∠D

Доказать: АВ = DC

CM ǁ АВ

D

А

M

АВCM – параллелограмм АВ = МС

АВ = DС

Δ МCD – равнобедренный МС = DC

∟

∟

Признаки равнобедренной трапеции

Если в трапеции диагонали равны , то она равнобедренная

С

В

АВСD – трапеция

АС = ВD

Доказать: АВ = DC

BN⏊AD

CM⏊AD

BN = CM

D

А

N

M

Δ ABN = Δ DCM

AM = DN

Δ AСМ = Δ DBN

AN = DM

AB = DC

ǁ

ǁ

ǁ

Если в трапеции диагонали равны , то она равнобедренная

С

В

2-й способ

АВСD – трапеция

АС = ВD

Доказать:

АВ = DC

M

D

СМ ǁ ВD

А

ΔAСМ – равнобедр

ВСМD -параллелограмм

(BD=СМ = АС)

СМ = BD

∠ М = ∠СAМ

∠ М = ∠АDB

ΔABD = ΔDCA

(1 признак)

АВ = DC

∠ ADB = ∠СAD

ǁ

ǁ

ǁ

Еще одно свойство!

С

В

О – точка пересечения диагоналей АС и BD

О

M

D

А

BO = BD – DO

∠ ADB = ∠СAD

CO = AC – AO

ΔAOD – равнобедренный

AO = DO

ВO = СO

Задачи по чертежам

1 .

В

С

Дано: АВСD – трапеция

Найти: ∠АОВ

О

D

А

∟

ǁ

ǁ

Задачи по чертежам

2 .

Дано:

АВСD – трапеция

Найти:

углы трапеции

В

С

ǁ

α

α

α

D

А

Задачи по чертежам

3 .

В

С

Дано: АВСD – трапеция

ВЕ ǁ СD

Найти: углы трапеции

75 0

40 0

А

Е

D

45 0

135 0

Задачи по чертежам

4 .

В

С

Дано:

АВСD – трапеция

AD = 30

Найти: ВС

D

30

А

ǁ

ǁ

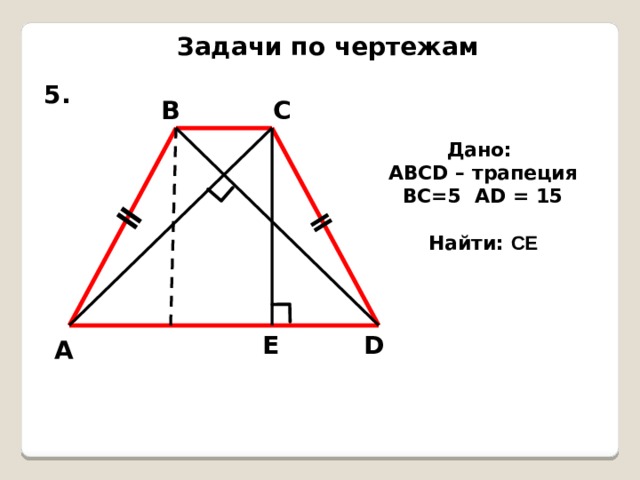
Задачи по чертежам

5.

В

С

Дано:

АВСD – трапеция

ВС=5 АD = 15

Найти: CЕ

Е

D

А

ǁ

ǁ

Задачи по чертежам

6.

В

С

Дано:

АВСD – трапеция

ВС=5 АD = 15

Найти: Р АВСD

30 0

О

60 0

D

А

Е

ǁ

ǁ

Задачи по чертежам

7.

В

С

Дано:

АВСМ – трапеция

ВС=5 АМ = 7

Найти: CМ

60 0

60 0

Р

М

К

А

ǁ

Задачи по чертежам

8 .

Дано:

АВСD – трапеция

Найти: ∠С

С

В

ǁ

50 0

А

D

ǁ

ǁ

Задачи по чертежам

9 .

Дано:

АВСD – трапеция

ВC = а, ED = b

Найти: АЕ и АD

В

С

Е

А

К

D

ǁ

ǁ

ǁ

ǁ

Терема Фалеса

Если на одной из двух прямых отложить последовательно несколько равных отрезков и через их концы провести параллельные прямые, пересекающие вторую прямую, то они отсекут на второй прямой равные между собой отрезки

В 1

С

А 1

Дано:

А 1 А 2 =А 2 А 3 =А 3 А 4 =А 4 А 5 =…

А 1 В 1 ǁА 2 В 2 ǁА 3 В 3 ǁА 4 В 4 ǁА 5 В 5 ǁ…

Доказать:

В 1 В 2 =В 2 В 3 =В 3 В 4 =В 4 В 5 =…

В 2

А 2

А 3

В 3

D

А 4

В 4

Через точку В 2 проведем c ǁ a

В 5

А 5

a

b

c

ǁ

ǁ

ǁ

ǁ

Задачи по чертежам

10 .

А

Дано:

АА 1= А 1 А 2 =А 2 А 3 =А 3 А 4 =А 4 А 5 =…

А 1 В 1 ǁА 2 В 2 ǁА 3 В 3 ǁА 4 В 4 ǁА 5 В 5 ǁ…

АВ 4 = 20

Найти: В 2 В 3

А 1

В 1

А 2

В 2

В 3

А 3

А 4

В 4

В 5

А 5

ǁ

ǁ

Задачи по чертежам

11 .

В

Дано: ЕК ǁ АС

Найти: Р АВС

К

Е

4

5

12

А

С

ǁ

ǁ

Задачи по чертежам

12 .

Дано:

АВСD – трапеция

Доказать: АО = СО

В

С

М

К

О

А

D

ǁ

ǁ

Задачи по чертежам

13 .

Дано:

АВСD – трапеция

МКǁВЕǁСD

AD=16

Найти: АК

10

В

С

М

D

А

Е

К