Тригонометрия вокруг нас

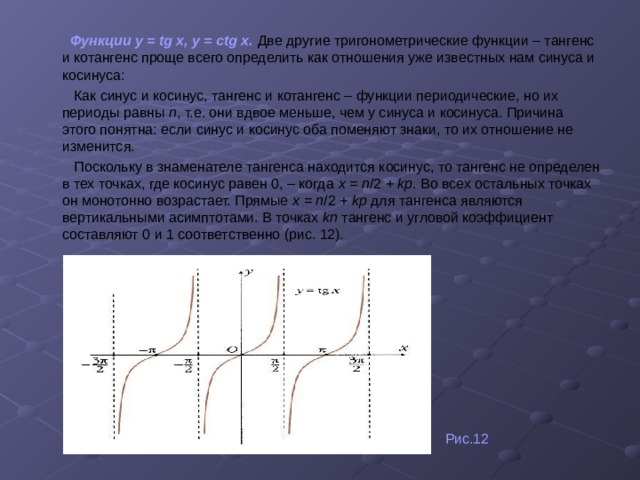
Функции у = tg х, у = ctg х. Две другие тригонометрические функции – тангенс и котангенс проще всего определить как отношения уже известных нам синуса и косинуса:

Как синус и косинус, тангенс и котангенс – функции периодические, но их периоды равны п , т.е. они вдвое меньше, чем у синуса и косинуса. Причина этого понятна: если синус и косинус оба поменяют знаки, то их отношение не изменится.

Поскольку в знаменателе тангенса находится косинус, то тангенс не определен в тех точках, где косинус равен 0, – когда х = п /2 + kp . Во всех остальных точках он монотонно возрастает. Прямые х = п /2 + kp для тангенса являются вертикальными асимптотами. В точках kп тангенс и угловой коэффициент составляют 0 и 1 соответственно (рис. 12).

Рис.12

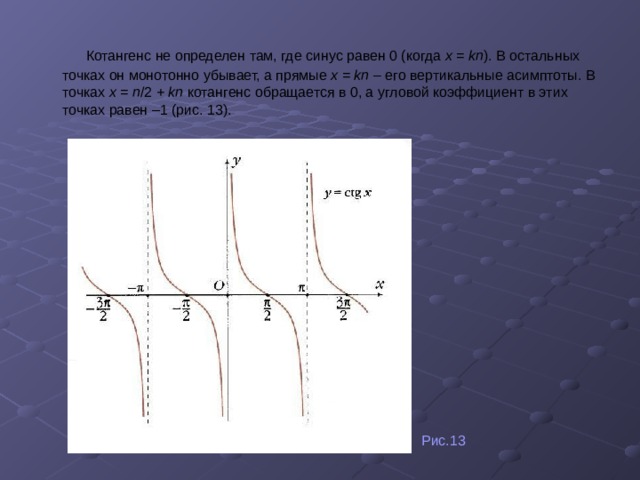
Котангенс не определен там, где синус равен 0 (когда х = kп ). В остальных точках он монотонно убывает, а прямые х = kп – его вертикальные асимптоты. В точках х = п /2 + kп котангенс обращается в 0, а угловой коэффициент в этих точках равен –1 (рис. 13).

Рис.13

Кто придумал тригонометрические функции?

Тригонометрические функции возникли впервые в связи с исследованиями в астрономии и геометрии. Соотношения отрезков в треугольнике и окружности, являющиеся по существу тригонометрическими функциями, встречаются уже в 3 в. до н. э. в работах математиков Древней Греции – Евклида, Архимеда, Аполлония Пергского и других, однако эти соотношения не являлись самостоятельным объектом исследования, так что тригонометрические функции как таковые ими не изучались. Они рассматривались первоначально как отрезки и в такой форме применялись Аристархом (конец 4 – 2-я половина 3 вв. до н. э.), Гиппархом (2 в. до н. э.), Менелаем (1 в. н. э.) и Птолемеем (2 в. н. э.) при решении сферических треугольников. Птолемей составил первую таблицу хорд для острых углов через 30' с точностью до 10–6. Это была первая таблица синусов. Как отношение функция sin a встречается уже у Ариабхаты (конец 5 в.). Функции tg a и ctg a встречаются у аль-Баттани (2-я половина 9 – начало 10 вв.) и Абуль-Вефа (10 в.), который употребляет также sec a и cosec a. Ариабхата знал уже формулу (sin2a + cos2a) = 1, а также формулы sin и cos половинного угла, с помощью которых построил таблицы синусов для углов через 3°45'; исходя из известных значений тригонометрических функций для простейших аргументов. Бхаскара (12 в.) дал способ построения таблиц через 1 с помощью формул сложения. Формулы преобразования суммы и разности тригонометрических функций различных аргументов в произведение выводились Региомонтаном (15 в.) и Дж. Непером в связи с изобретением последним логарифмов (1614). Региомонтан дал таблицу значений синуса через 1'. Разложение тригонометрических функций в степенные ряды получено И.Ньютоном (1669). В современную форму теорию тригонометрических функций привел Л.Эйлер (18 в.). Ему принадлежат их определение для действительного и комплексного аргументов, принятая ныне символика, установление связи с показательной функцией и ортогональности системы синусов и косинусов.

А бывают ли обратные функции?

Обра́тные тригонометри́ческие фу́нкции — математические функции, являющиеся обратными к тригонометрическим функциям. К обратным тригонометрическим функциям обычно относят шесть функций:

аркси́нус (обозначение: arcsin)

аркко́синус (обозначение: arccos)

аркта́нгенс (обозначение: arctg; в иностранной литературе arctan)

арккота́нгенс (обозначение: arcctg; в иностранной литературе arccotan)

арксе́канс (обозначение: arcsec)

арккосе́канс (обозначение: arccosec; в иностранной литературе arccsc)

Название обратной тригонометрической функции образуется от названия соответствующей ей тригонометрической функции добавлением приставки «арк-» (от лат. arc — дуга). Это связано с тем, что геометрически значение обратной тригонометрической функции можно связать с длиной дуги единичной окружности (или углом, стягивающим эту дугу), соответствующей тому или иному отрезку. Изредка в иностранной литературе пользуются обозначениями типа sin−1 для арксинуса и т.п.; это считается неоправданным, так как возможна путаница с возведением функции в степень −1.

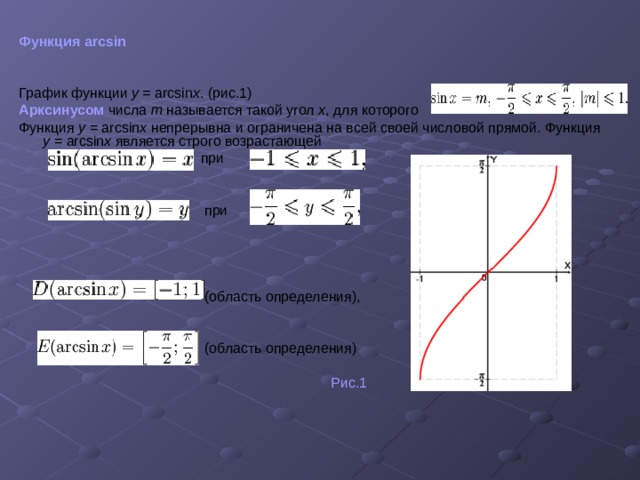
Функция arcsin

График функции y = arcsin x . (рис.1)

Арксинусом числа m называется такой угол x , для которого

Функция y = arcsin x непрерывна и ограничена на всей своей числовой прямой. Функция y = arcsin x является строго возрастающей .

при

при

(область определения),

(область определения)

Рис.1

Свойства функции arcsin :

• (функция является нечётной)

• при

• при х = 0

• при

• .
• .

Получение функции arcsin

Дана функция y = sin x . На всей своей области определения она является кусочно-монотонной, и, значит, обратное соответствие y = arcsin x функцией не является. Поэтому мы рассмотрим отрезок, на котором она строго возрастает и принимает все значения области значений — .

Так как для функции y = sin x на интервале каждому значению аргумента соответствует единственное значение функции, то на этом отрезке существует обратная функция y = arcsin x , график которой симметричен графику функции y = sin x на отрезке относительно у = х

Функция arccos.

График функции y = arccos x . (рис.2)

Арккосинусом числа m называется такой угол x , для которого

Функция y = arccos x непрерывна и ограничена на всей своей числовой прямой. Функция y = arccos x является строго убывающей.

• cos(arccos x ) = x при
• arccos(cos y ) = y при
• D (arccos x ) = [ − 1;1], (область определения),
• E (arccos x ) = [0;π]. (область значений).

Рис.2

0 при arccos x = 0 при x = 1. . . Получение функции arccos Дана функция y = cos x . На всей своей области определения она является кусочно-монотонной, и, значит, обратное соответствие y = arccos x функцией не является. Поэтому мы рассмотрим отрезок, на котором она строго возрастает и принимает все свои значения — [0;π]. На этом отрезке y = cos x строго монотонно убывает и принимает все свои значения только один раз, а значит, на отрезке [0;π] существует обратная функция y = arccos x , график которой симметричен графику y = cos x на отрезке [0;π] относительно прямой y = x . " width="640"

Свойства функции arccos.

• arccos( − x ) = π − arccos x (функция центрально-симметрична относительно точки

• arccos x 0 при
• arccos x = 0 при x = 1.

• .
• .

Получение функции arccos

Дана функция y = cos x . На всей своей области определения она является кусочно-монотонной, и, значит, обратное соответствие y = arccos x функцией не является. Поэтому мы рассмотрим отрезок, на котором она строго возрастает и принимает все свои значения — [0;π]. На этом отрезке y = cos x строго монотонно убывает и принимает все свои значения только один раз, а значит, на отрезке [0;π] существует обратная функция y = arccos x , график которой симметричен графику y = cos x на отрезке [0;π] относительно прямой y = x .

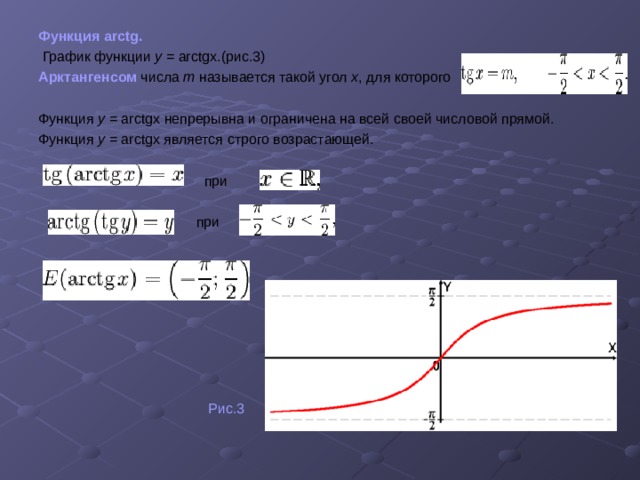
Функция arctg.

График функции y = arc tg x . (рис.3)

Арктангенсом числа m называется такой угол x , для которого

Функция у = arctgx непрерывна и ограничена на всей своей числовой прямой.

Функция у = arctgx является строго возрастающей.

при

при

Рис.3

0. при x = 0. при x . . " width="640"

Свойства функции arctg .

• (функция нечётная).
• при x 0.
• при x = 0.
• при x
• .
• .

Получение функции arctg.

Дана функция у = tg. На всей своей области определения она является кусочно-монотонной, и, значит, обратное соответствие у = arctg функцией не является. Поэтому рассмотрим отрезок, на котором она строго возрастает и принимает все свои значения только один раз —

На этом отрезке у = tg строго монотонно возрастает и

принимает все свои значения только один раз, следовательно, на интервале существует обратная функция у = arctg , график которой симметричен графику у = tg на отрезке относительно прямой y = x .

Функция arcctg .

Арккотангенсом числа m называется такой угол x , для которого

Функция y = arcctg непрерывна и ограничена на всей своей числовой прямой.

Функция y = arcctg является строго убывающей.

• при
• при 0 y
• .
• .

Свойства функции arcctg. Рис. 4

• . ,график функции центрально-симметричен относительно точки
• . при любых х.
• .

Получение функции arcctg.

Дана функция y = ctg x . На всей своей области определения она является кусочно-монотонной, и, значит, обратное соответствие y= arcctg x функцией не является. Поэтому рассмотрим отрезок, на котором она строго возрастает и принимает все свои значения только один раз — (0;π). На этом отрезке y = ctg x строго возрастает и принимает все свои значения только один раз, следовательно, на интервале (0;π) существует обратная функция y= arcctg x , график которой симметричен графику y = ctg x на отрезке (0;π) относительно прямой y = x .

Где применяются функции ?

Тригонометри́ческие фу́нкции — математические функции от угла. Они важны при изучении геометрии, а также при исследовании периодических процессов. Обычно тригонометрические функции определяют как отношения сторон сторон прямоугольного треугольника или длины определённых отрезков в единичной окружности. Более современные определения выражают тригонометрические функции через суммы рядов или как решения некоторых дифференциальных уравнений, что позволяет расширить область определения этих функций на произвольные вещественные числа и даже на комплексные числа.

Тригонометрические функции применяются очень хорошо в науке и технике. В первую очередь там, где для расчетов используются угловые величины. Например, в механике, оптике, а также там, где используются колебательные процессы - физике. При изучении электромагнитных явлений, радиосвязи, теории упругости, явлениях резонанса, и т.д. и т.п.