| Государственное бюджетное общеобразовательное учреждение Самарской области средняя общеобразовательная школа №2 им. В. Маскина ж.-д. ст. Клявлино Муниципального района Клявлинский Самарской области |
| Исследовательская работа по теме: |
| «Мир удивительных чисел»
Номинация: За страницами учебника математики. |
|
|
| Работу выполнили: Андреева Ангелина и Ломоносова Александра, ученицы 6 класса ГБОУ СОШ №2 им. В. Маскина ж.-д. ст. Клявлино |
| ![]() учитель математики учитель математики
|
Содержание:
Введение…………………………………………………….3-4
Глава 1. Из истории чисел ………………………………….5
Глава 2. Простые числа
2.1 Простые числа. Решето Эратосфена……………………6
2.2 Числа – близнецы………………………………………..6
Глава 3.Фигурные числа
3.1 Фигурные числа………………………………………..7-8
3.2 Многоугольные числа…………………………………8-9
Глава 4. Дружественные, совершенные, компанейские числа
4.1 Дружественные числа…………………………………9-10
4.2 Совершенные числа…………………………………..10-11
4.3Исследование дружественных и совершенных чисел..11-12
4.4 Компанейские числа ……………………………………12
Заключение …………………………………………………12-13
Литература…………………………………………………..13
Приложения…………………………………………………14
Введение
«Числа правят миром» – Пифагор
Мир без чисел…Возможно ли это? В современной жизни мы используем числа, даже не задумываясь об этом. Идем в магазин, смотрим на часы, набираем телефонный номер. Без чисел невозможно ни одно научное открытие. Одна ошибка в расчетах и космический корабль просто не взлетит. Не случайно открытие числа – одно из самых гениальных проявлений человеческого разума.
Самые древние по происхождению числа натуральные. Но, оказывается, среди натуральных чисел есть: простые, числа - близнецы, совершенные, дружественные, фигурные, компанейские числа. Именно они являются родоначальниками всех натуральных чисел.
Проблема состоит в том, что многие школьники предмет математика считают трудным и не интересным, их мнение отражается на результатах обучения.
Актуальность работы заключается в возможности получения интересной информации о числах.
Теоретическая значимость нашей работы заключается в том, что многие одноклассники и не только, возможно обратят внимание на наше исследование. Практическая значимость работы состоит в том, что она может быть использована школьниками для повышения математической грамотности при изучении предмета математика.
Цель: как можно больше отыскать удивительных натуральных чисел, рассмотреть их свойства и закономерности.
Предлагаемая работа является результатом поиска удивительных и необычных чисел, проведенного по литературным источникам.
Задачи:1. Рассмотреть основные этапы развития натуральных чисел.
2. Выделить интересные виды удивительных натуральных чисел: простые, фигурные, совершенные, дружественные, компанейские числа - близнецы.
3. Составить памятку для учащихся 6-х классов
Объект исследования – простые, фигурные, совершенные, дружественные, компанейские числа.
Предмет исследования - натуральные удивительные числа и их свойства.
При выполнении работы были использованы следующие приемы и методы: опрос (анкетирование), анализ (статистическая обработка данных), работа с источниками информации, исследование.
Практическая значимость заключается в возможности применения итогов исследования на уроках математики и во внеурочной деятельности.
Гипотеза: Интересная информация о числах, заинтересует моих одноклассников и возможно они будут более углубленно изучать математику, что повысит их математическую грамотность и результативность обучения.
Для того чтобы выяснить, знают ли современные школьники интересные числа, был проведен тестовый опрос.
Мы провели анкетирование среди 6-х классов нашей школы. Задавали два вопроса:
1.Знакомы ли вам дружественные, совершенные, фигурные, компанейские, числа – близнецы?
2. Хотели бы узнать больше об этих числах и о тех, что не знакомы вам?
В опросе приняли участие 37 человек. Результаты опроса представлены в виде таблицы и отражены в столбчатой диаграмме) (Приложение I):
| Понятие числа | знают |
| натуральные | 100% |
| числа – близнецы | 0% |
| совершенные | 54% |
| дружественные | 54% |
| компанейские | 46% |
| фигурные | 35% |
| простые | 84% |
Учащиеся пожелали узнать об этих числах больше.
Проведя статистическую обработку данных, мы сделали вывод, что учащиеся знают не все понятия, поэтому необходимо сделать для учеников 6-х классов памятки «Удивительный мир чисел», чтобы повысить их математическую грамотность.
Основная часть: Глава 1. Из истории чисел Первые цифры
На папирусе ли, на глине ли, на камне ли, но людям необходимо было изображать числа. И тут, был сделан весьма важный шаг: люди догадались писать вместо группы единиц один знак. Сначала это был знак числа 10. Например, египтяне обозначали десяток знаком  (единицу они обозначали простой вертикальной черточкой
(единицу они обозначали простой вертикальной черточкой  , как это делаем мы). А десять десятков, то есть сотню, обозначали
, как это делаем мы). А десять десятков, то есть сотню, обозначали  . Появились знаки и для тысячи (
. Появились знаки и для тысячи (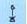 - цветок лотоса), десятка тысяч (
- цветок лотоса), десятка тысяч ( - поднятый кверху палец), ста тысяч (
- поднятый кверху палец), ста тысяч (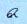 - сидящая лягушка) и миллиона (
- сидящая лягушка) и миллиона (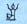 - человек с поднятыми руками).
- человек с поднятыми руками).
Чтобы записать какое-нибудь число, египетский писец бесхитростно писал столько раз знак тысяч, сколько было тысяч в числе, затем знак сотен столько раз, сколько в нем было сотен (кроме уже написанных тысяч), знак десятков столько раз, сколько было в числе десятков, и, наконец, знак единиц столько раз, сколько в нем было единиц. Похожим образом обозначали числа на острове Крит, расположенном в Средиземном море.
Народы (Вавилона, Шумера), жившие в Междуречье Тигра и Евфрата в период от II в. до н.э. до начала нашей эры, использовали только два клинописных знака - прямой клин  (1) и лежащий клин
(1) и лежащий клин  (10). Например, число 23 изображалось так:
(10). Например, число 23 изображалось так: 
В Древней Руси числа обозначали буквами, над которыми ставили специальный знак - титло. Большие числа славяне записывали так:
1000 - 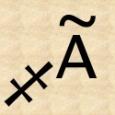 , 3000 -
, 3000 - 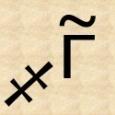 . Знак
. Знак  обозначал тысячи. Число 10000 обозначали той же буквой, что и 1, но без титла, и ее обводили кружком. Называлось это число "тьма". Отсюда и выражение "тьма народу".
обозначал тысячи. Число 10000 обозначали той же буквой, что и 1, но без титла, и ее обводили кружком. Называлось это число "тьма". Отсюда и выражение "тьма народу".
Глава 2. Простые числа
2.1 Простые числа. Решето Эратосфена
Простое число - натуральное число, имеющее два делителя: 1 и само число. Числа, имеющее более двух делителей называются составными. Единичка же не считается ни простым числом, ни составным.
Небольшую "коллекцию" простых чисел можно составить старинным способом придуманный ещё в 3 в. до н. э. Эратосфеном Киренским, хранителем знаменитой Александрийской библиотеки.
Выпишем несколько подряд идущих чисел, начиная с 2. Двойку отберём в свою коллекцию, а остальные числа, кратные 2, зачеркнем. Ближайшим не зачёркнутым числом будет 3. Возьмём в коллекцию и его, а все остальные числа, кратные 3, зачеркнем. При этом окажется, что некоторые числа уже были вычеркнуты раньше, как, например, 6, 12 и др. Следующее наименьшее не зачёркнутое число – это 5. Берем пятерку, а остальные числа, кратные 5,зачеркиваем. Повторяя эту процедуру снова и снова, в конце концов, добьемся того, что не зачеркнутыми останутся одни лишь простые числа – они словно просеялись сквозь решето. Поэтому такой способ и получил название "решето Эратосфена".

Простых чисел бесконечное множество.
2.2 Числа – близнецы
Два простых числа, которые отличаются на 2, как 5 и 7, 11 и 13, 17 и 19, получили название "близнецы". В натуральном ряду имеется даже "тройня" - это числа 3, 5, 7. Ну а сколько всего существует близнецов - современной науке неизвестно.
В пределах первой сотни близнецы – это следующие пары чисел: (3, 5), (5, 7), (11, 13), (17, 19), (29, 31), (41, 43), (59, 61), (71,73). По мере удаления от нуля близнецов становится все меньше и меньше. Близнецы могут собираться в скопления, образуя четверки, например, (5, 7, 11, 13) или (11, 13, 17, 19). Как много таких скоплений – тоже пока неизвестно.
Глава 3. Фигурные числа
3.1 Фигурные числа
Давным-давно, помогая себе при счете камушками, люди обращали внимание на правильные фигуры, которые можно выложить из камушков. Можно просто класть камушки в ряд: один, два, три. Если класть их в два ряда, чтобы получались прямоугольники, то получаются все четные числа. Можно выкладывать камни в три ряда: получатся числа, делящиеся на три.

Фигурные числа — общее название чисел, связанных с той или иной геометрической фигурой.
Различают следующие виды фигурных чисел:
Линейные числа — числа, которые делятся только на единицу и на самих себя и, следовательно, представимы в виде последовательности точек, выстроенных в линию: 1, 2, 3, 5, 7, 11, 13, 17, 19, 23, …
Плоские числа — числа, представимые в виде произведения двух сомножителей, то есть составные: 4, 6, 8, 9, 10, 12, 14, 15, …
Телесные числа — числа, представимые произведением трёх сомножителей: 8, 12, 16, 18, 20, 24, 27, 28, …

3.2 Многоугольные числа
Выкладывая различные правильные многоугольники, можно получить разные классы многоугольных чисел. Предположительно от фигурных чисел возникло выражение: "Возвести число в квадрат или в куб".
Последовательность треугольных чисел: 1, 3, 6, 10, 15, 21, 28, 36, 4 и т.д. (1, 1+2=3, 1+2+3=6, 1+2+3+4=10, 1+2+3+4+5=15 и т. д.)

Квадратные числа представляют собой произведение двух одинаковых натуральных чисел, то есть являются полными квадратами: 1, 4, 9, 16, 25, 36, и т.д. (1+3=4, 1+3+5=9, 1+3+5+7=16).
Пятиугольные числа 1, 5, 12, 22, 35, 51, 70, 92, 117, 145
Пирамидальные числа возникают при складывании круглых камушков горкой так, чтобы они не раскатывались. Получается пирамида. Каждый слой в такой пирамиде - треугольное число. Наверху один камушек, под ним - 3, под теми - 6 и т.д.: 1, 1+3=4, 1+3+6=10, 1+3+6+10=20, ...


Кубические числа возникают при складывании кубиков: 1, 2·2·2=8, 3·3·3=27, 4·4·4=64, 5·5·5=125... и так далее.
Глава 4. Дружественные, совершенные, компанейские числа
4.1 Дружественные числа
Дружественные числа - это такая пара натуральных чисел А и В, что число А есть сумма всех натуральных делителей числа В, меньших В; а число В есть сумма всех натуральных делителей числа А, меньших А.
Первая пара различных наименьших дружественных чисел 220 и 284:
220=1+2+4+71+142,
284=1+2+4+5+10+11+20+22+44+55+110;
была известна еще древнегреческому ученому Пифагору (6 в. до н.э.). Весьма вероятно, что он первым обратил на них внимание. Пифагорейцы считали их символом дружбы. Пифагор говорил: "Мой друг тот, кто является моим вторым я, как числа 220 и 284".
История изучения дружественных чисел
В IX веке арабский математик Сабит ибн Корра (абу Хасан Сабит ибн Корра ибн Марван аль Харрани) - врач, астроном - нашел общий способ получения дружественных чисел.
Теорема Сабита: Если все три числа p=3×2n-1-1, q=3×2n-1, r=9×22n-1-1 – простые, то числа А=2n×p×q и B=2n×r – дружественные.
При n=2 это пара чисел, найденная Пифагором.
n=4: числа 17 296 и 18 416;
n=7: числа 9 363 584 и 9 437 056.
Открытие второй (n=4) и третьей (n=7) пары дружественных чисел ранее приписывалось к открытию их в 1636 французским юристом и математиком Пьером Ферма и Декарту соответственно, однако оказалось, что она была известна за три с половиной столетия до них.
После периода малозначительных работ существенного продвижения в решении этой проблемы добился Леонард Эйлер, который в 1747-1750 гг. указал сразу 59 пар дружественных чисел. Он получил утверждение, очень похожее на теорему Сабита, но чуть более общее. Правда, не смог с помощью него найти новых дружественных чисел, т.к. в то время таблицы простых чисел были составлены только до 100 000.
Лишь А. Лежандр и российский ученый П.Л.Чебышев, используя новый критерии простоты чисел, сумели обнаружить с помощью теоремы Эйлера еще одну пару дружественных чисел.
Поразительное открытие в 1867 г. (в некоторых источниках указана дата - 1887) сделал 16-летний итальянец Николо Паганини (тезка знаменитого скрипача), обнаружив вторую по величине пару дружественных чисел 1184 и 1210 (ближайшую к 220 и 284), которую проглядели все знаменитые математики, изучавшие дружественные числа, чем потряс весь математический мир.
В настоящее время известны все пары дружественных чисел. В основном их находят сейчас при помощи компьютера.
| Приведем первые 12 пар дружественных чисел:
220 и 284 6232 и 6368; 63020 и 76084;
1184 и 1210; 10744 и 10856; 66928 и 66992;
2620 и 2924; 12285 и 14595; 67095 и 71145;
5020 и 5564; 17296 и 18416; 69615 и 87633. |
|
|
|
|
|
4.2 Совершенные числа
Совершенным называется число, равное сумме всех своих делителей (включая 1, но исключая само число). Наименьшее из совершенных чисел 6 равно сумме трех своих делителей 1, 2 и 3. Следующее совершенное число 28=1+2+4+7+14.
Первым крупным достижением теории совершенных чисел была теорема Евклида о том, что число 2n-1(2n-1) - четное и совершенное, если число 2n-1 - простое. Лишь две тысячи лет спустя Эйлер доказал, что формула Евклида содержит все четные совершенные числа.
Формула Евклида позволяет без труда доказывать многочисленные свойства совершенных чисел. Например, все совершенные числа треугольные. Это значит, что, взяв совершенное число шаров, мы всегда сможем сложить из них равносторонний треугольник. Из той же формулы Евклида следует другое любопытное свойство совершенных чисел: все совершенные числа, кроме 6, можно представить в виде частичных сумм ряда кубов последовательных нечетных чисел 13+33+53+… Еще более удивительно, что сумма величин, обратных всем делителям совершенного числа, включая его самого, всегда равна 2. Например, взяв делители совершенного числа 28, получим:
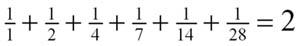


4.3.Исследование дружественных и совершенных чисел.
І. Проверим, что каждое из чисел 1184 и 1210 равно сумме делителей другого числа, не считая его самого.
Найдем делители чисел 1184 и 1210.
Делители 1184: 1;2;4;8;16;32;37;74;148;296;592.
Вычислим сумму делителей числа 1184: 1+2+4+8+16+32+37+74+148+296+592= 1210.
Делители 1210: 1;2;5;10;11;22;55;110;121;242;605.
Вычислим сумму делителей числа 1210: 1+2+5+10+11+22+55+110+121+242+605= 1184.
Делаем вывод: сумма делителей числа 1184 равна числу 1210, а сумма делителей числа 1210 равна числу 1184, значит, числа 1184 и 1210 являются дружественными.
ІІ. По теореме Евклида 2n-1(2n-1) , при n= 5 мы нашли число 496, при n=7 число 8128. Проверим, что эти числа равны сумме всех своих делителей, не считая самого числа.
Найдем делители числа 496: 1;2;4;8;31;16;62;124;248.
Вычислим сумму его делителей 1+2+4+8+16+31+62+124+248 = 496.
Найдем делители числа 8128: 1;2;4;8;16;32;64;127;254;508;1016;2032;4064.
Вычислим сумму его делителей 1+2+4+8+16+32+64+127+254+508+1016+2032+4064 = 8128.
Вывод: сумма всех делителей этих чисел, не считая самого числа, равна самому числу, значит, это есть совершенные числа.
4.4 Компанейские числа
Понятия совершенных и дружественных чисел часто упоминаются в литературе по занимательной математике. Однако почему-то мало говорится о том, что числа могут дружить и компаниями. Понятие компанейских чисел хорошо раскрывается в англоязычных источниках.
Компанейскими называется такая группа из k чисел, в которых сумма собственных делителей первого числа равна второму, сумма собственных делителей второго – третьему и т.д. А первое число равно сумме собственных делителей k-го числа.
Есть компании по 4, 5, 6, 8, 9 и даже 28 участников, а вот по три не найдено. Пример пятёрки, пока единственной известной: 12496, 14288, 15472, 14536, 14264.
ЗАКЛЮЧЕНИЕ
В результате изучения различных источников мы познакомились с удивительными натуральными числами: фигурными, совершенными, дружественными, простыми, компанейскими, числами - близнецами.
Предметом исследования стали совершенные и дружественные числа.
При выполнении работы было доказано, что 1184 и 1210 являются дружественными числами, а числа 496; 8128 – совершенными.
Анализ наших решений показал, что простые числа – это «кирпичики», из которых строятся все натуральные числа, «перекладывая» их, можно получить удивительные «числовые сооружения».
Эта работа вызвала у нас интерес, и мы надеемся, что она заинтересует и других учащихся. Мы познакомим одноклассников с нашим исследованием с целью повышения их математической культуры. Результаты работы мы оформили в памятку, которую предложим всем своим одноклассникам и 6-иклассникам. Она и поможет приобрести полезную и интересную информацию о числах.
Выводы:
Знание удивительных натуральных чисел позволит расширить кругозор, математическую культуру и интерес учащихся к математике.
В школьных учебниках нет понятий всех этих чисел, поэтому результат данной работы – памятка « Удивительный мир чисел» будет очень полезной для учащихся 6-х классов.
Литература
1.Кордемский Б.А. Удивительный мир чисел: Книга для учащихся/ М.: «Просвещение», 1995
2.Депман И.Я. За страницами учебника математики: Пособие для учащихся 5-6 классов средней школы/- М.: «Просвещение», 1989
3.Я.И. Перельман. Занимательная математика: Е.: Издательство «Тезис», 1994
4.Я. Познаю мир. Детская энциклопедия: Математика/ Я 11 Авт.-сост. А.П. Савин и др.: - М.: ООО "Издательство АСТ", 2001.
5.Г.И.Гейзер. История математики в школе. Пособие для учителей. – М.: Просвещение, 1981.
6.Internet ресурсы
ПРИЛОЖЕНИЯ
ПРИЛОЖЕНИЕ I
Вопросы:
1.Знакомы ли вам дружественные, совершенные, фигурные, компанейские, числа – близнецы?
2. Хотели бы узнать больше об этих числах и о тех, что вам не знакомы?
![]()








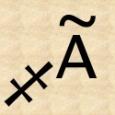 , 3000 -
, 3000 - 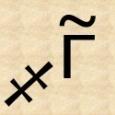 . Знак
. Знак  обозначал тысячи. Число 10000 обозначали той же буквой, что и 1, но без титла, и ее обводили кружком. Называлось это число "тьма". Отсюда и выражение "тьма народу".
обозначал тысячи. Число 10000 обозначали той же буквой, что и 1, но без титла, и ее обводили кружком. Называлось это число "тьма". Отсюда и выражение "тьма народу". 

















