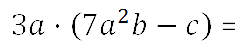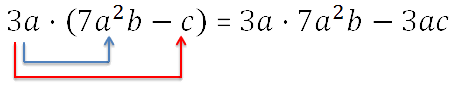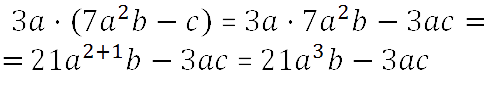Умножение одночлена на многочлен

Умножение одночлена на многочлен

Всем здравствуйте!

На прошлом уроке мы начали такую важную тему как действия с многочленами и поговорили о первых таких простых действиях как сложение и вычитание. Следующее на очереди, конечно же, умножение. И начнём мы с наиболее простого случая: будем умножать многочлен на одночлен. Т. е. будем умножать многочлен на многочлен, состоящий из одного слагаемого. 

Рассмотрим такой пример:

(3х³ – 2х + 1) ⋅ 3х²

3х³ – 2х + 1 – многочлен.

3х² – одночлен.

По сути, мы должны с вами раскрыть скобки, т. е. применить распределительный закон. Напоминаю, как этот закон применятся: умножить каждое слагаемое в скобках на то, на что умножается скобка. В данном случае, всё, что стоит в скобках, умножаем на 3х².

(3х³ – 2х + 1) ⋅  3х² = 3х ³⋅ 3х² – 2х ⋅  3х² + 1 ⋅ 3х²

Теперь мы должны вспомнить правило умножения одночленов: перемножаем числовую часть и каждую букву отдельно, не забываем свойство степени. Получаем:

(3х³ – 2х + 1) ⋅ 3х² = 3х³ ⋅ 3х² – 2х ⋅ 3х² + 1 ⋅ 3х² = 9х⁵ – 6х³ + 3х²

Правило: чтобы умножить одночлен на многочлен нужно умножить этот одночлен на каждый член исходного многочлена, после чего полученные произведения сложить.

По сути, мы просто раскрываем скобки.

Пример:

3х(7х – 2) – 2х(5х – 3)

Нужно раскрыть скобки, первая скобка раскрывается просто: мы 3х умножаем на 7х и на –2, а вот перед второй скобкой стоит знак минус, здесь ещё нужно поменять знаки в скобке на противоположные. После раскрытия скобок привести подобные.

Приступим:

3х(7х – 2) – 2х(5х – 3) = 3х ⋅ 7х – 3х ⋅ 2 – 2х ⋅ 5х – 2х ⋅  (–3) = 21х² – 6х – 10х² +6х = 11х²

Пример: упростить выражение и найти его значение при а = –20.

3 ⋅ (1,6а² – 0,5а + 1,4) – 4 ⋅ (1,2а² + 0,6а + 0,3)

Раскроем скобки и приведём подобные слагаемые:

3 ⋅ (1,6а² – 0,5а + 1,4) – 4 ⋅ (1,2а² + 0,6а + 0,3) = 4,8а² – 1,5а + 4,2 – 4,8а² – 2,4а – 1,2 = –3,9а + 3

При а = –20 имеем –3,9 ⋅ (–20) + 3 = 81

Пример: не выполняя умножения, т. е. не раскрывая скобок, найти степень многочлена.

–3x²(4x⁸ – 2x⁵ + x) и его старший коэффициент. Степень: 11, коэффициент: –12.

А если рассмотреть многочлен –3x³(4x⁸ – 2x⁵ + 4x⁸)? Степень: 8, коэффициент: 6.

Сегодня мы с вами поговорили о том, как умножать многочлен на одночлен. Впереди умножение многочлена на многочлен.

До встречи.

ВИДЕО УРОК ДОСТУПЕН ПО ССЫЛКЕ

https://resh.edu.ru/subject/lesson/1164/

Запомните!

Чтобы умножить многочлен на одночлен, нужно каждый член многочлена умножить на этот одночлен с учетом правила знаков.

Рассмотрим пример умножения многочлена на одночлен.

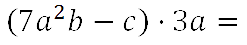
1. Для удобства запишем одночлен перед многочленом, используя переместительный закон умножения.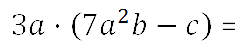

2. Теперь умножим одночлен на каждый одночлен в скобках отдельно, не забывая правило знаков.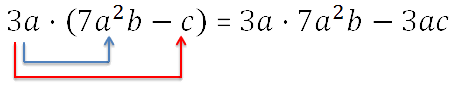

3. Запишем окончательное решение: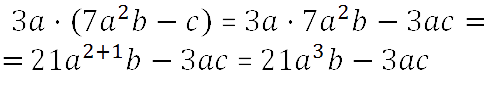

Важно!

Будьте внимательны при определении знака результата умножения!

Обязательно помните правило знаков.

Примеры умножения многочлена на одночлен

• 6a(3a − b) = 6a · 3a − 6ab = 18a^{1 + 1} − 6ab = 18a² − 6ab

• −4a(−a + b) = (−4a) · (−a) − 4ab = 4a · a − 4ab = 4a^{1 + 1} − 4ab = 4a² − 4ab

• xyz(x² + 2y² −3z²) = xyz · x² + xyz · 2y² − xyz · 3z² = x^{2 + 1}yz + 2xy^{2 + 1}z −3xyz^{2 + 1} =
  = x³yz + 2xy³z − 3xyz³

Проверь себя

• 8x³(6x² – 4x + 3) = ………………….……= 48x⁵ – 32x⁴ + 24x³

• 5a²(2a² + 3a – 7) = …………………...…..= 10a⁴ + 15a³ – 35a²

• 3y(9y³ – 4y² – 6) = ………………………. =27y⁴ – 12y³ – 18y

• 6b⁴(6b² + 4b – 5) = ………….……………= 36b⁶ + 24b⁵ – 30b⁴