Урок алгебры в 10 классе
по теме «Тригонометрические уравнения».
Учитель: Макарова С.В.
Урок рекомендован молодым специалистам, учителям математики.
Йошкар – Ола, 2018 год
УМК: Алгебра и начала анализа. 10 – 11 классы: В двух частях. Ч.1. Учебник для учащихся общеобразовательных учреждений (базовый уровень) / А.Г.Мордкович. – 13-е изд., стер. – М.: Мнемозина, 2012, рекомендовано МО и науки РФ.
Ч.2. Задачник для учащихся общеобразовательных учреждений (базовый уровень) / А.Г.Мордкович. – 13-е изд., стер. – М.: Мнемозина, 2012, рекомендовано МО и науки РФ.
Профиль: общеобразовательный (4 часа в неделю)
Тип урока: урок обобщения и систематизации знаний
Педагогическая технология: здоровье сберегающая технология, технология уровневой дифференциации, технология сотрудничества.
Методы обучения: частично – поисковый; системные обобщения, тестовая проверка уровня знаний, исследовательский. самопроверка, самооценка.
Цель: Повторить, обобщить, систематизировать и углубить знания о методах решения тригонометрических уравнений.
Задачи:
Образовательные:
Закрепить умение классифицировать уравнения по методам решения;
Научить решать тригонометрические уравнения, выбирая для каждого соответствующий метод решения;
Учить извлекать информацию, представленную в разных формах.
Развивающие:
Развивать логическое мышление, математическую речь;
Развивать умение применять приемы сравнения, обобщения, выделения главного;
Расширять кругозор учащихся, повышать познавательную активность учащихся на уроках математики;
Развитие умения аргументировано участвовать в обсуждении решений.
Воспитательные:
Формирование коммуникативных способностей учащихся;
Воспитание ответственности, активности, самостоятельности, умение работать в коллективе;
Воспитание умения внимательно слушать и оценивать устную информацию, воспитание умения четко формулировать свои мысли, воспитание коммуникативных способностей, воспитание аккуратности, умение слушать одноклассников.
Оборудование: доска, карточки для индивидуальной и дифференцированной работы, тест с выбором ответов, компьютер, проектор, экран.
Формируемые УУД:
Коммуникативные:
Развивать у учащихся представление о месте математики в системе наук;
Развивать умение точно и грамотно выражать свои мысли, отстаивать свою точку зрения в процессе дискуссии;
Поддерживать инициативное сотрудничество в ходе индивидуальной и групповой работы;
Организовывать и планировать учебное сотрудничество с учителем и сверстниками;
Уметь выслушивать мнение одноклассников, не перебивая их;
Воспринимать текст с учетом поставленной учебной задачи, находить в тексте информацию, необходимую для решения.
Регулятивные:
Формировать целевые установки учебной деятельности, выстраивать последовательности необходимых операций (алгоритм действий);
Удерживать цель деятельности до получения ее результата;
Корректировать деятельность: вносить изменения в процесс с учетом возникших трудностей и ошибок, намечать способы их устранения;
Оценивать уровень владения учебным действием (отвечать на вопрос «что я не знаю и не умею»);
Определять последовательность промежуточных целей с учетом конечного результата;
Критически оценивать полученный ответ, осуществлять самоконтроль, проверяя ответ на соответствие условию.
Познавательные:
Выполнять учебные задачи, не имеющие однозначного решения;
Ориентироваться на разнообразие способов решения задач;
Владеть общим приемом решения учебных задач;
Воспроизводить по памяти информацию, необходимую для решения учебной задачи;
Осуществлять поиск необходимой информации для выполнения учебных заданий;
Уметь устанавливать причинно-следственные связи.
Личностные:
Формирование познавательного интереса;
Формирование устойчивой мотивации к изучению и закреплению изученного материала;
Формирование мотивации к аналитической деятельности (к анализу);
Формирование навыков составления алгоритма выполнения задания, навыков организации своей деятельности;
Формирование навыка осознанного выбора наиболее эффективного способа решения.
Ожидаемые результаты: Подтвердить имеющиеся базовые знания в соответствии с тематикой урока, знать основные виды тригонометрических уравнений и уметь их решать, используя изученные методы.
Формы организации учебной деятельности: индивидуальная, индивидуально – дифференцированная, фронтальная, групповая.
К концу занятия обучающиеся смогут:
анализировать методы решения уравнений;
применять методы решения уравнений к тригонометрическим уравнениям;
распознавать методы решения тригонометрических уравнений;
формулировать алгоритмы решения тригонометрических уравнений в зависимости от метода.
Ход урока:
Орг. момент.
Друзья мои! Я очень рада приветствовать сегодня вас.
И для меня уже награда вниманье ваших умных глаз
Я знаю, каждый из вас гений,
Но без труда талант не впрок
Решайте тригонометрические уравнения
И вместе сочиним урок!
Мои соавторы и судьи!
Не накажу оценкой вас
И знания закрепим сейчас.
Французский писатель Анатоль Франс однажды заметил: «Учиться можно только весело… Чтобы переварить знания, надо поглощать их с аппетитом». Давайте будем следовать этому совету писателя, будем активны, внимательны, всё будем делать с удовольствием и большим желанием.
Тема нашего сегодняшнего урока: «Решение тригонометрических уравнений». Мы с вами повторяем, обобщаем, приводим в систему изученные виды, типы, методы и приёмы решения тригонометрических уравнений.
Перед вами задача – показать свои знания и умения по решению тригонометрических уравнений.
Устная работа.
Работа с определениями, терминами, понятиями.
Давайте вспомним некоторые тригонометрические понятия, решим кроссворд (На экран проецируется сетка кроссворда и вопросы к нему. Обучающиеся работают парами). При правильном решении кроссворда по вертикали можно прочитать ключевое слово нашего урока.
|
|
| 1. |
|
|
|
|
|
|
| 2. |
|
|
|
|
|
|
|
| 3. |
|
|
|
|
|
|
|
| 4. |
|
|
|
|
|
|
|
|
|
|
| 5. |
|
|
|
|
|
|
|
|
| 6. |
|
|
|
|
|
|
| 7. |
|
|
|
|
|
|
|
|
|
| 8. |
|
|
|
| 9. |
|
|
|
|
|
|
По горизонтали:
1.Ордината точки на единичной окружности? (синус).
2.2пn для функций у= sinx, y=cosx? (период).
3. Угловая величина дуги, длина которой равна её радиусу (радиан).
4.Формулы вида sin(2π+x), cos(π-x)… называются? (приведения).
5.Абсцисса точки на единичной окружности? (косинус).
6.Сумма квадратов синуса и косинуса одного аргумента равна…?(единица).
7. Число из отрезка [0; π/2] синус которого равен а называется…? (арксинус).
8.Математическая постоянная 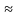 3,14? (пи).
3,14? (пи).
9. Отношение синуса числа к косинусу того же числа (тангенс).
Ключевое слово урока: уравнение.
2) Работа с формулами простейших тригонометрических уравнений.
Учитель показывает карточки, учащиеся продолжают запись. Записывают в тетради либо корни уравнения, либо по корням исходное уравнение.





tg x = - 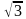
cos x = 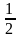
cos x = - 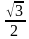
sin x = 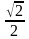
sin x = - 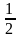
Карточки:





cos x = a
sin x = - 1
x=2πn, n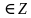
sin x = 1
tg x = a




x = πn, n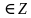
cos x = - 1
x = 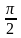 +πn, n
+πn, n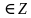
sin x = a
Ребята, а для чего нам нужны простейшие тригонометрические уравнения? (Вывод делают сами учащиеся)
3)Классификация тригонометрических уравнений. Объяснить устно решение следующих тригонометрических уравнений:
2sin2x +sinx – 1 =0; (Это уравнение приводится к алгебраическому путем введения новой переменной и сведению его к квадратному уравнению)
5sin2x + 6cosx – 6 =0; (Это уравнение приводится к алгебраическому путем замены sin2x через основное тригонометрическое тождество, введения новой переменной и сведению его к квадратному уравнению.)
tgx – 2ctgx + 1 = 0; (Это уравнение приводится к алгебраическому путем замены ctgх = 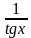 , tgх
, tgх = πn, n
= πn, n Z, введения новой переменной и сведению его к квадратному уравнению.)
Z, введения новой переменной и сведению его к квадратному уравнению.)
3sin2x + sinxcosx = 2cos2x; (Однородное уравнение второй степени, решается делением обеих частей уравнения на cos2x или sin2x.)
5sinx – 6cosx = 0; (Однородное уравнения первой степени, решается делением обеих частей уравнения на cosx или sinx.)
sin2x – cosx = 0; (Это уравнение решается разложением на множители. При решении таких уравнений нужно пользоваться правилом: произведение нескольких множителей равно нулю, если хотя бы один из них равен нулю, а остальные при этом имеют смысл.)
cos5x – cos3x = 0. (Это уравнение решается с помощью разложения разности тригонометрических функций в произведение.)
4) Найди ошибку. На доске записано уравнение. Нужно найти ошибки в решении и объяснить, почему они были допущены.
sin2x + 2cosx – sinx – 1 = 0;
2sinxcosx + 2cosx – (sinx + 1) = 0;
2cosx(sinx + 1) – (sinx + 1) = 0;
(sinx + 1)(2cosx – 1) =0;
sinx + 1 = 0 или 2cosx – 1 = 0
sinx = - 1 2cosx = - 1
x = 3π/2 + πn, n Z x =
Z x =  2π/3 + 2πn, n
2π/3 + 2πn, n Z
Z
Физкультминутка.
Кто живет у нас в квартире.
Раз, два, три, четыре,
(Хлопаем в ладоши.)
Кто живет у нас в квартире? (Шагаем на месте.)
Раз, два, три, четыре, пять, (Прыжки на месте.)
Всех могу пересчитать:
(Шагаем на месте.)
Папа, мама, брат, сестра,
(Хлопаем в ладоши.)
Кошка Мурка, два котенка, (Наклоны туловища влево-вправо.)
Мой сверчок, щегол и я –
(Повороты туловища влево-вправо.)
Вот и вся моя семья.
(Хлопаем в ладоши.)
Решение уравнений.
Решение с указанием чёткого алгоритма решения уравнений данного типа.
1) Решить уравнение 1 – 3sinxcosx – 5cos2x = 0
Алгоритм:
1. Приведение к однородному уравнению.
2. Деление левой и правой части на cos2x при условии cosx 0.
0.
3. Решение квадратного уравнения.
4. Подстановка.
5. Решение простейших тригонометрических уравнений.
Ответ:

2. Найти наибольший отрицательный корень уравнения 2sin22x+5sin2x – 3 =0
Алгоритм:
1. Замена переменной.
2. Решение квадратного уравнения.
3. Решение простейших тригонометрических уравнений.



Ответ: Наибольший отрицательный корень 
3. Найти сумму корней уравнения sin5x+sinx= sin3x, принадлежащих промежутку (0;π)
sin3x, принадлежащих промежутку (0;π)
Алгоритм:
1.Применить формулу перехода от суммы тригонометрических выражений к произведению.
2.Разложить на множители, путем вынесения общего множителя за скобки.
3.Решение простейших тригонометрических уравнений.
















Найдем сумму 
Ответ: 2π
Разно уровневая самостоятельная работа. Тест.
Уровень А.
Вариант 1.
1.Решите уравнение 2cos2х = 3sinx.
А.  + 2πn, n
+ 2πn, n Z.
Z.
Б. (-1)n∙ +πn, n
+πn, n Z.
Z.
В. (-1)n+1  +πn, n
+πn, n Z.
Z.
Г. (-1)n+1  +πn, n
+πn, n Z.
Z.
2.Решите уравнение 1 – 4sin2x = 0. Найдите сумму его корней, принадлежащих промежутку [0; 2 ].
].
А.  . Б. 4π. В. 2π. Г.
. Б. 4π. В. 2π. Г.  .
.
Вариант 2.
1.Решите уравнение 2sin2x – 5 = -5cosx.
А. πn, n Z.
Z.
Б. π+2πn, n Z.
Z.
В. 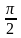 + 2πn, n
+ 2πn, n Z.
Z.
Г. 2πn, n Z.
Z.
2.Решите уравнение 3 – 4cos2х = 0. Найдите сумму его корней, принадлежащих промежутку [0; 3π]
А. 4π. Б. 9π. В. 6π. Г. 7,5π.
Уровень В.
Вариант 1.
1.Найти наименьший положительный корень уравнения
sinx + sin5x = 0.
А. π/6. Б. π/4.
В. π /3. Г. π/2.
2.Решите уравнение 3sin2x + sinxcosx = 2cos2x.
Вариант 2.
1.Найдите наименьший положительный корень уравнения cosx + cos5x = 0
А. π/6 В. π/4
Б. π/2 Г. π
2.Решите уравнение 4sin2x = 3sinxcosx + cos2x/
Рефлексия.
Закончите предложения:
Сегодня я понял(а), что мне необходимо…
При решении тригонометрических уравнений важно…
Самое трудное для меня…
Меня удивило…
Было интересно…
Итог урока. Домашнее задание.
Чем занимались на уроке?
Что интересное узнали на уроке?
Пожалуйста, поднимите руку те, кто считает, что эту тему понял очень хорошо?
Кто считает, что ещё нужно поработать?
Кто совсем плохо понял эту тему?
Дома:
1. Повторить основные формулы решения простейших тригонометрических уравнений, методы решения тригонометрических уравнений.
2.Домашняя работа выбирается самими обучающимися по уровням.
Уровень А.
Уровень В.
Спасибо за урок!







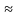 3,14? (пи).
3,14? (пи).




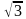
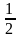
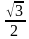
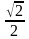



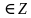




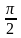 +πn, n
+πn, n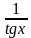 , tgх
, tgх









