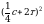Федеральное государственное казенное общеобразовательное учреждение
«Средняя общеобразовательная школа № 6»
Открытый урок
алгебры в 7 классе
« ВОЗВЕДЕНИЕ В КВАДРАТСУММЫ И
РАЗНОСТИ ДВУХ ВЫРАЖЕНИЙ»
Учитель математики
Гоибова Ольга Михайловна.
Тип урока: урок изучения нового материала (урок-исследование)
Вид урока: проблемно-поисковый.
Цели урока: Слайд 2
Образовательные:
-вывести формулы квадратов суммы и разности двух чисел.
-сформировать умение учащихся практически применять эти формулы для упрощения выражений.
Развивающие :
-развивать логическое мышление, внимание, память, сообразительность, культуру математической речи и культуру общения;
Воспитывающие:
-воспитывать ответственное отношение к деятельности, высокой познавательной активности и самостоятельности;
-воспитывать интерес к математике как учебному предмету через современные технологии преподавания;
- воспитывать чувство ответственности, культуры диалога.
Формы организации познавательной деятельности:
фронтальная, индивидуальная, групповая, коллективная.
Методы и приёмы обучения:объяснительно-иллюстративный, проблемно-поисковый, исследовательский, словесный, наглядный (демонстрация компьютерной презентации), практический.
Оборудование :
-компьютер, мультимедийный проектор, экран, портрет Евклида, набор геометрических фигур, раздаточный материал.
Средства обучения:
Программное обеспечение:
MicrosoftOfficeWord 2007 MicrosoftOfficeWord 2010
Microsoft Office Power Point 2007 Microsoft Office Power Point 2010
План урока Слайд 3
Организационный момент.
Актуализация опорных знаний(устная работа).
Изучение нового материала (исследовательская работа)
Первичное закрепление материала.
Геометрический смысл формул квадрата суммы двух выражений.
Динамическая пауза.
Закрепление изученного материала.
Проверка усвоения изученного материала (первичный контроль знаний).
Домашнее задание.
Подведение итога урока.
| п/п | Название современных образовательных технологий, применяемых в УВП | Этапы урока/занятия (мероприятия), на которых технология применяется |
| 1. | Проблемная ситуация. | Этап 2. Этап 4. |
| 2. | Здоровьесберегающие технологии. | Этап 5. |
| 3. | Элементы технологии сотрудничества. | Этап 6. |
| 4. | Информационные технологии | При показе слайдов. |
| 5. | Рефлексия. | Этап 8. |
,
Т ехнологическая карта урока
ехнологическая карта урока
| Этап урока | Деятельность учителя | Деятельность ученика | Формируемые УУД |
| I . Орг момент. . Орг момент. | Отметить отсутствующих, ознакомить обучающихся с целью урока, активизировать к работе. Сообщение темы и цели урока. | Приветствуют учителя.Знакомство с темой урока | Коммуникативные: Подготовка к уроку. |
| II. Актуализация знаний.
| Задает вопросы на повторение. Упор на ранее сформированные знания. | Отвечают на поставленные вопросы. | Коммуникативные: планирование учебного сотрудничества с учителем и сверстниками Регулятивные:целеполагание |
| III. .Изучение нового материала (Исследовательская работа). | знакомит с планом урока.Таблица. Упростите выражения I столбца, запишите ответы в III столбце, проанализируйте результат 1 вариант -1), 2), 3)2 вариант - 4), 5), 6) - Мы с вами нашли наиболее простой способ умножения суммы и разности двух выражений на себя, т.е. вывели формулы возведения в квадрат суммы и разности двух выражений. -Эти формулы называются формулами сокращенного умножения, они применяются для упрощения выражений, для рационального решения некоторых числовых выражений. ПЕРВИЧНОЕ ЗАКРЕПЛЕНИЕ.Геометрический смысл формул квадрата суммы двух выражений.
| Слушают учителя, готовятся к восприятию материала. Раскрывают скобки по правилу умножения многочлена на многочлен (столбец I), полученные ответы записывают в Ш столбце таблицы. II часть таблицы закрыта. (а+b)2 =а2+2аb+b2(a-b)2=a2-2ab+b2 -формулируют эти формулы словесно. C помощью рисунка объясняют геометри- ческий смысл формулы (а+ b)2 = а2 + 2аb + b2. -Объясняют геометрический смысл выражения (а+в)2 (квадрат со стороной a+b). У каждого ученика – вырезанные из бумаги 2 квадрата со сторонами а и b и 2 прямоугольника со сторонами a иb).Каждый моделирует свой квадрат.
| Познавательные: поиск и выделение необходимой информации; учатся самостоятельно выделять и формулировать познавательную цель; построение логической цепи рассуждений; выдвижение гипотез и их обоснование. Коммуникативные: сотрудничество в поиске ответов на вопросы. Регулятивные:формирование целеустремленности и настойчивости в достижении целей,готовности к преодолению трудностей. |
| IV. Динамическая пауза.
| Гимнастика для глаз. | Снимают физическое напряжение, выполняя гимнастику для глаз. | Личностные : Знание основных норм здоровой жизни и ориентация на их выполнение.
|
| V.Закрепление изученного материала
| Записывает примеры. Работа у доски и в тетрадях. При выполнении заданий проговаривать правила 1 .№ 862 (а, г, е, з). 2.Вычислить: (30+1)2 ; 512 ; (30-1)2 ; 492 3. Преобразовать выражения : (а-7)2 ; (7-а)2 ; (5+х)2 ; (-5-х)2
| Решают примеры у доски и в тетрадях. При выполнении заданий - проговаривают правила Учащиеся сами приходят к выводу: (а - b)2 =(b - а)2 (-а - b)2 =(а + b) 2 | Познавательные :учатся в процессе реальной ситуации использовать определение «квадрат суммы и разности». Регулятивные: учатся обрабатывать информацию и ранжировать ее по указанным основаниям. Коммуникативные : Осуществляют взаимоконтроль, оказывают взаимопомощь. |
| VI. Этап предварительного к онтроля.(карточки) онтроля.(карточки) | Работа по карточкам | Соединяют пары тождественно равных выражений. Вспоминают определение тождественно равных выражений.
| Личностные: организовывают свою деятельность, т.е. ставят личные цели, учатся их достигать и оценивать результаты. Познавательные :учатся в процессе реальной ситуации использовать определение «квадрат суммы и разности». |
| VII. Домашнее задание. | Инструктаж по домашнему заданию:п. 31, доказать геометрический смысл формулы (a-b)2, №863(а, б, в, д); 866, №869( д , е). Слайд 28
| Записывают задание.
| Личностные : Индивидуальный выбор учащихся. |
| VIII.Подведение итогов. | Подводит итоги, -С какими формулами мы познакомились сегодня на уроке? -Почему эти формулы называются формулами сокращенного умножения? -Чему равен квадрат суммы двух выражений? -Чему равен квадрат разности двух выражений? -Как вы думаете, зачем нужны нам эти формулы и стоит ли их запоминать? (С помощью формул результат можно получить гораздо проще и быстрее). Рефлексия. Дифференцированное выставление оценок.
| Заканчивают фразы.
Учащиеся анализируют свою работу на уроке, обсуждают, высказывают свое мнение выводы. | Коммуникативные: умение с достаточной полнотой и точностью выражать свои мысли. Познавательные: умение структурировать знание.Личностные : рефлексия способов и условий действия, контроль и оценка процесса и результатов деятельности. |
Директор ФГКОУ «СОШ № 6» Турсунова М. Т.

Х од урока.
од урока.
I.Организационный момент.Вступительное слово учителя.
Эпиграф урока:
Знание только тогда знание,
когда оно приобретено усилиями
своей мысли, а не памятью.
Слайд 4 (Л.Н.Толстой)
«Ещё в глубокой древности было подмечено, что некоторые многочлены можно умножать короче, быстрее, чем остальные. Так появились формулы сокращённого умножения. Их несколько. Сегодня вам предстоит сыграть роль исследователей и «открыть» две из этих формул».
Итак, тема нашего урока квадрат суммы и квадрат разности двух выражений. Чтобы открыть формулы нам необходимо, вспомнить, что мы знаем и умеем.
II. Актуализация опорных знаний (устные упражнения)
1.Прочитайте выражения. Слайд 5
а) а + b ; г) x – у ; б) n2 + m2 ; д) (z –a)2;
в) (c + d)2 ; е) b2 – c2; ж) 2ху.
- что значит: (c + d)2 ; (z –a)2(значит, выражение умножается на себя два раза)
2. Найдите квадраты выражений: a; - 2 ; 5b ; 4х2, 6х2 у3. Слайд 6
(вспомнить правило возведения в степень произведения).
3. Представьте в виде квадрата: 64; 100; 36а2; 25x4; 49 b2c2; х6с8. Слайд 7
4. Найдите удвоенное произведение выражений: Слайд 8
а) а и b; б) 3b и -5с; в) 0,4х и 2х2; г) 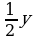 и 6 .
и 6 .
(вспомнить правило умножения степеней с одинаковыми степенями).
5. Перемножьте данные многочлены: Слайд 9
а) (x +2) ·(y - 1) б) ( 3 – c) · (4 + b)
(вспомнить правило умножения многочлен на многочлен)
6.Вычислить значения выражений 25²+250+5²; 13²- 78+3². Слайд 10
2 ученика считают у доски. Учитель предлагает вычислить, используя калькулятор.
- Возможно ли сосчитать устно? (В конце урока ответим на этот вопрос)
III.Изучение нового материала (Исследовательская работа).
1. Упростите выражения I столбца, запишите ответы в III столбце, проанализируйте результат. Слайд 11
1 вариант -1), 2), 3) 2 вариант - 4), 5), 6)
Ученики раскрывают скобки по правилу умножения многочлена на многочлен (столбец I), полученные ответы записывают в Ш столбце таблицы. II часть таблицы закрыта.
| № | I | II | III |
| 1) 2) 3) 4) 5) 6) 7) 8) | (y + b) (y +b) (с + d ) (c +d) (х + 2)(х+2) (x – y) (x – y) (m - n) (m- n) (a – 2) (a – 2) (6х +y) (6x+y) (5 – 4b) (5 – 4b) | (y +b)2 (c + d)2 (х+2)2 (x – y)2 (m-n)2 (a – 2)2
| y2 + 2yb + b2 c2 + 2cd + d2 х2+ 4х + 4 x2 – 2xy + y2 m2 – 2mn + n2 a2 – 4a + 4
|
- Ребята, посмотрите внимательно на I и III столбики. Слайд 12
Ребята, посмотрите внимательно на I и III столбики. Слайд 12
- Есть ли в них нечто общее?Можно ли выражения Icтолбца записать короче? (Ответы учащихся) (Открыть II столбец). Слайд 12
Есть ли в них нечто общее?Можно ли выражения Icтолбца записать короче? (Ответы учащихся) (Открыть II столбец). Слайд 12
-Что получается в результате умножения суммы и разности двух выражений?
-Результатом умножения является трехчлен, у которого:
1 -й член – квадрат первого выражения;
-й член – квадрат первого выражения;
2-й член – удвоенное произведение первого и второго выражений;
3-й член – квадрат второго выражения.
- Мы с вами нашли наиболее простой способ умножения суммы и разности двух выражений на себя, т.е. вывели формулы возведения в квадрат суммы и разности двух выражений.
-Записать ответы заданий 7) и 8) столбца I в столбцах II и III найденным способом. Слайд 13
-Скажите, как проще и быстрее вам было работать: перемножая многочлен на многочлен или применяя формулы?
-Попробуйте записать формулы, которыми будем пользоваться для возведения в квадрат суммы и разности двух выражений. Слайд 14
(а+b)2 =а2+2аb+b2(a-b)2=a2-2ab+b2
- Чем они отличаются? (знаком перед удвоенным произведением).
-Сформулируйте эти формулы словесно. Слайд 15
-Эти формулы называются формулами сокращенного умножения, они применяются для упрощения выражений, для рационального решения некоторых числовых выражений.
Примеры применения формул. Слайд 16
2.Чтение правил по учебнику, парный пересказ правил .
3. Первичное закрепление .
Заполнить таблицу. Слайд 17
| Выражение
| Квадрат 1 выражения | Удвоенное произведение | Квадрат 2 выражения | Итог
|
| (а + 4)2 |
|
|
|
|
| (8 - х)2 |
|
|
|
|
| (2y + 1)2 |
|
|
|
|
| (0,5b - 2)2 |
|
|
|
|
4. . Вставьте пропущенные одночлены: Слайд 18
( * – 1)2 = 9х2 - * х + 1; (5а + * )2 = * а2 + 40а + 16
5. Геометрическое истолкование формулы (а+b)2.Слайд 19
-Некоторые правила сокращённого умножения были известны ещё около 4 тыс. лет тому назад. Их знали вавилоняне и другие народы древности. Тогда они формулировались словесно или геометрически.
У древних греков величины обозначались не числами или буквами, а отрезками прямых. Они говорили не «а2», а «квадрат на отрезке а», не «а∙b», а «прямоугольник, содержащийся между отрезками а и b». Например, тождество (а+ b)2 = а2 + 2аb + b2во второй книге «Начал» Евклида (3 в до н.э.) формулировалось так: «Если отрезок как-либоразбит на два отрезка, то площадь квадрата, построенного на всем отрезке, равна сумме площадей квадратов, построенных на каждом из двух отрезков, и удвоенной площади пря-моугольника, сторонами которого служат эти два отрезка». Доказательство опиралось на геометрическое соображение.
А теперь давайте и мы с помощью рисунка объясним геометрический смысл формулы (а+ b)2 = а2 + 2аb + b2.
-Объясните геометрический смысл выражения (а+в)2 (квадрат со стороной a+b). (У каждого ученика – вырезанные из бумаги 2 квадрата со сторонами а и b и 2 прямоугольника со сторонами a иb).Каждый моделирует свой квадрат.
- Чему равна площадь полученного квадрата? (Сумме площадей квадрата со стороной а, двух площадей прямоугольника со сторонами а и в и площади квадрата со стороной в).

IV.Динамическая пауза.Почти 90% всей информации человек воспринимает глазами. Если устают глаза, снижается наше внимание и активность. Давайте перед следующей задачей дадим отдых глазам и себе.
1. Закройте глаза на несколько секунд, сильно напрягая глазные мышцы, затем раскройте их, расслабив мышцы. Повторите 3-4 раза.
2. Посмотрите на переносицу и задержите взор. Затем посмотрите вдаль. Повторите 3—4 раза.
3. Медленно наклоняйте голову: вперед—влево— вправо - назад. Повторите 3-4 раза.
4. Поморгайте несколько раз глазами, не напрягая мышц. Сделайте глубокий вздох и медленный выдох.
V .Закрепление изученного материала. Слайд 22 Работа у доски и в тетрадях. При выполнении заданий - проговаривать правила.
.Закрепление изученного материала. Слайд 22 Работа у доски и в тетрадях. При выполнении заданий - проговаривать правила.
1 .№ 862 (а, г, е, з).
2.Вычислить:
(30+1)2 ; 512 ; (30-1)2 ; 492 .
3. Преобразовать выражения : (а-7)2 ; (7-а)2 ; (5+х)2 ; (-5-х)2
Учащиеся сами приходят к выводу: (а - b)2 =(b - а) 2 , (-а - b)2 =(а + b) 2 Слайд 23
4. А теперь вернемся к числовым выражениям, которые в начале урока вычислялись учащимися с помощью калькулятора и решались по действиям в тетради. Делается вывод, что рационально можно найти значения данных выражений используя выведенные на уроке формулы сокращенного умножения. Слайд 24 (гиперссылка к слайду 10)
VI.Этап предварительного контроля.(карточки)
1.Соедините пары тождественно равных выражений. Слайд 25 (вспомнить определение тождественно равных выражений)
| 1. | ( 3а + с) 2 | 5. | ( y - в) 2 |
| 2. | ( а – 2в) 2 | 6. | x2 – 2xв + в2 |
| 3. | ( x – в) 2 | 7. | а2– 4ав + 4в2 |
| 4. | y2 – 2yв + в2 | 8. | 9а2 + 6ас + с2 |
2. Выбрать правильный ответ. Слайд 26
|
| (y - 9)2 | (5x+4y)2 | (2a – 0,5x)2 | 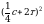
|
| 1 | y2 -9y +81 | 25x2 - 20xy +16 y2 | 4a2 - 2ax +0,25 x2 | 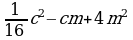
|
| 2 | y2 + 18y +81 | 25x2 + 40xy +16 y2 | 4a2 + 2ax +0,25 x2 | 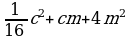
|
| 3 | y2 -18y +81 | 25x2 +20xy +16 y2 | 4a2 - ax +0,25 x2 | 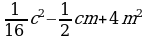
|
| 4 | y2 + 9y +81 | 25x2 - 40xy +16 y2 | 4a2 + ax +0,25 x2 | 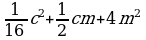
|
3. Вычислить : 612, 592Слайд 27
VII. Домашнее задание: п. 31, доказать геометрический смысл формулы (a-b)2,
№863(а, б, в, д); 866, №869( д , е). Слайд 28
VIII. Итог урока. Слайд 29
-С какими формулами мы познакомились сегодня на уроке?
-Почему эти формулы называются формулами сокращенного умножения?
-Чему равен квадрат суммы двух выражений?
-Чему равен квадрат разности двух выражений?
-Как вы думаете, зачем нужны нам эти формулы и стоит ли их запоминать?
(С помощью формул результат можно получить гораздо проще и быстрее).
Рефлексия. Выставление отметок.
Учащиеся анализируют свою работу на уроке, обсуждают, высказывают свое мнение.








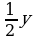 и 6 .
и 6 .