Урок геометрии по теме "Площадь многоугольника"

Урок геометрии по теме: «Площадь многоугольника»

Учитель математики

МБОУ средняя общеобразовательная школа №71 г. Рязани

Буланова Ольга Михайловна

Цель урока:

• Повторить понятие площади фигур, формулы вычисления площади.
• Повторить свойства площади.
• Систематизировать изученный материал в 8 и 9 классах.
• Проконтролировать степень усвоения ЗУН.

• Воспитательные задачи:
• Формирование мировоззрения:

показать, что источник возникновения изучаемой темы возник из практических потребностей людей.

• Формирование учебных навыков: а) внимания б) самоконтроля и контроля

в) трудолюбия г) самостоятельности д) честности

• Развивающие задачи:

а) развитие речи б) развитие мыслительной деятельности, умения анализировать, обобщать, классифицировать

Ход урока.

1.Оргмомент.

2. Воспроизведение и коррекция опорных знаний у учащихся.

а) Решение опорных задач.

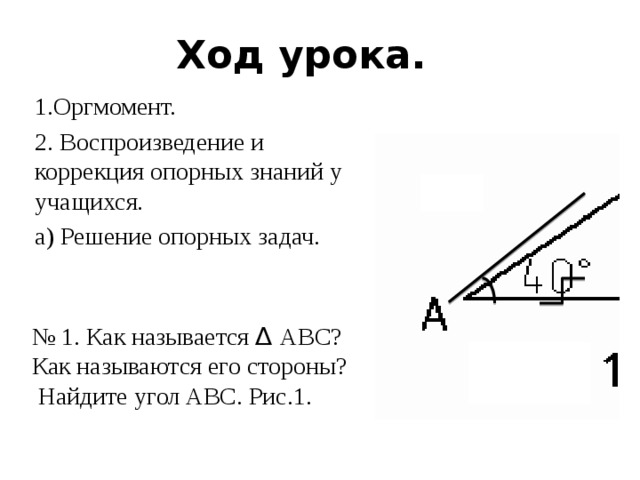
№ 1. Как называется  ∆ AВС? Как называются его стороны?

  Найдите угол ABC. Рис.1.

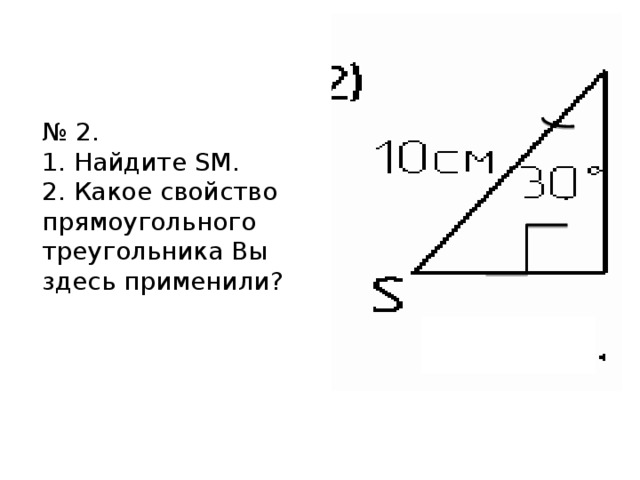
№ 2. 1. Найдите SM. 2. Какое свойство прямоугольного треугольника Вы здесь применили?

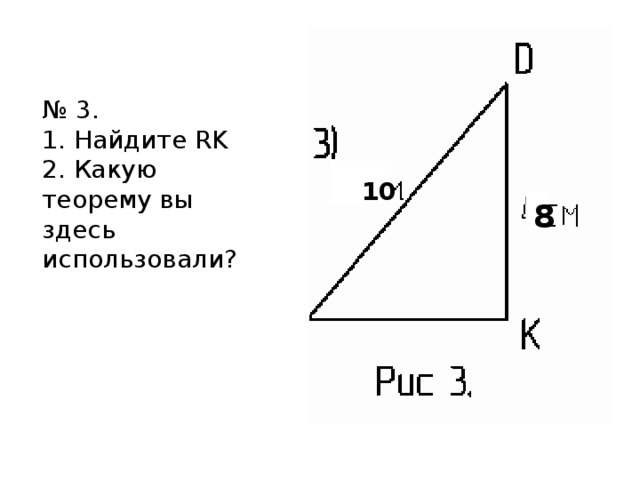
№ 3. 1. Найдите RK 2. Какую теорему вы здесь использовали?  

1111

10

8

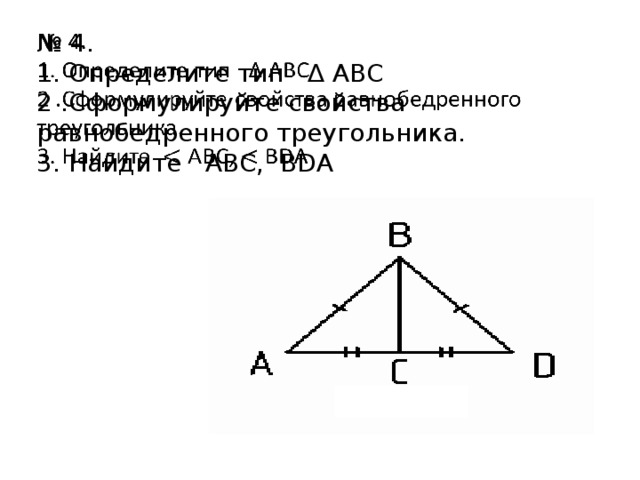
№ 4. 1. Определите тип ∆ АВС 2 .Сформулируйте свойства равнобедренного треугольника. 3. Найдите АВС, ВDА

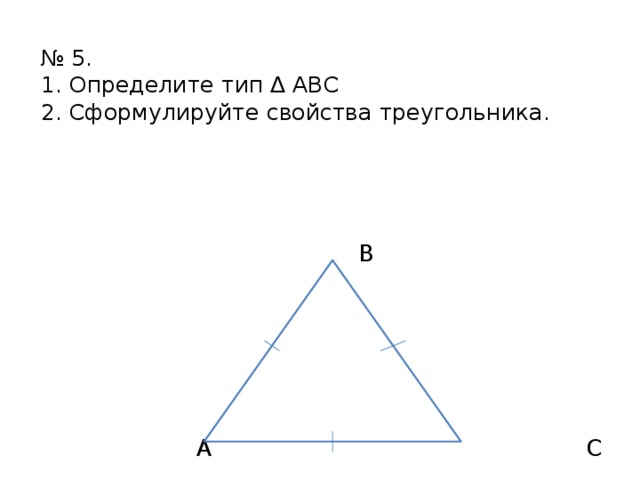
№ 5. 1. Определите тип ∆ АВС 2. Сформулируйте свойства треугольника.

B

A C

б) Повторение формул.

1.Сформируйте свойства площади многоугольников.

2. По какой из данных формул можно определить площадь треугольника? Параллелограмма? Ромба? Прямоугольника? Квадрата?

1) S = ab 2) S = ah 3) S = ½ ab 4) S = ½ d 1 d 2 5) S = a 2

3. Площади, каких фигур можно вычислить, используя следующие формулы:

S = * h, S = ab sin α

S = ½ d 2 , S =

S = ½ d 1 d 2 sin α, S =

в) Графический диктант.

Если утверждение верно «+», если неверно « - ».

• Подобные многоугольники имеют равные площади.

2. Диагональ параллелограмма делит его на два треугольника, площади которых равны.

3. Если многоугольник состоит из нескольких многоугольников, то его площадь равна сумме площадей этих многоугольников.

4. Площадь квадрата равна квадрату его диагонали.

5. Площадь параллелограмма равна произведению его смежных сторон.

6. Площадь прямоугольного треугольника равна произведению его катетов.

7. Если высоты двух треугольников равны, то их площади относятся как основания.

8. Если угол одного треугольника равен углу другого треугольника, то площади этих треугольников относятся как суммы сторон, заключающих равные углы.

9. Стороны параллелограмма обратно пропорциональны соответствующим высотам.

10. Среди ромбов с равными сторонами наибольшую площадь имеет квадрат .

Ответы:

- + + - - - + - + +

Критерий оценок:

«5» - за все правильные ответы

«4» - 1-2 ошибки

«3» - 3-4 ошибки

«2» - более 4 ошибок

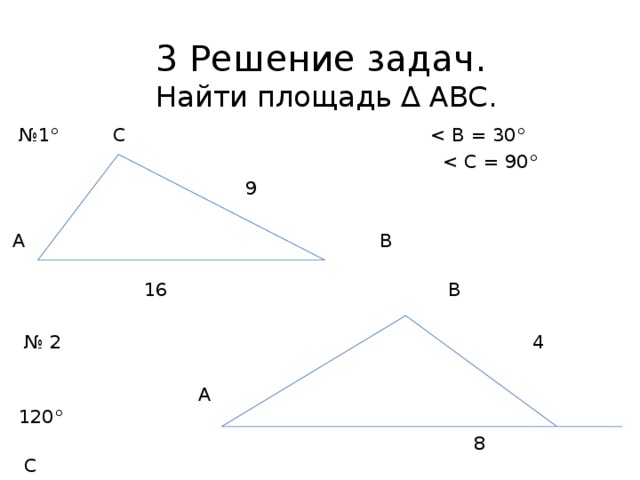
3 Решение задач. Найти площадь ∆ АВС.

№ 1° С

9

А В

16 В

№ 2 4

А 120°

8 С

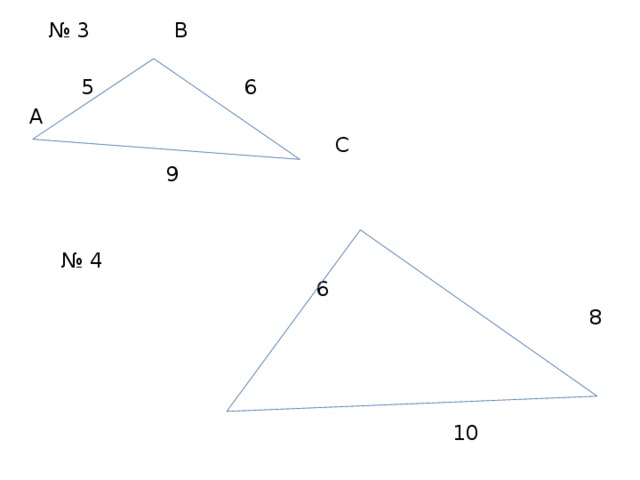
№ 3 В

5 6

А

С

9

№ 4

6

8

10

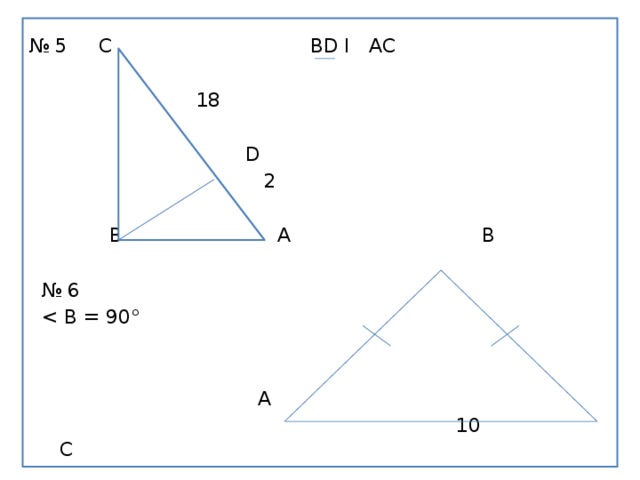
№ 5 С ВD І АС

18

D

2

В А В

№ 6

А

10 С

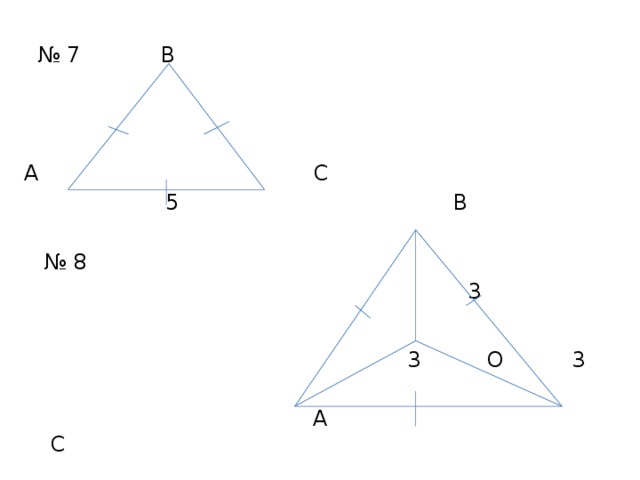
№ 7 В

А С

5 В

№ 8

3

3 О 3

А С

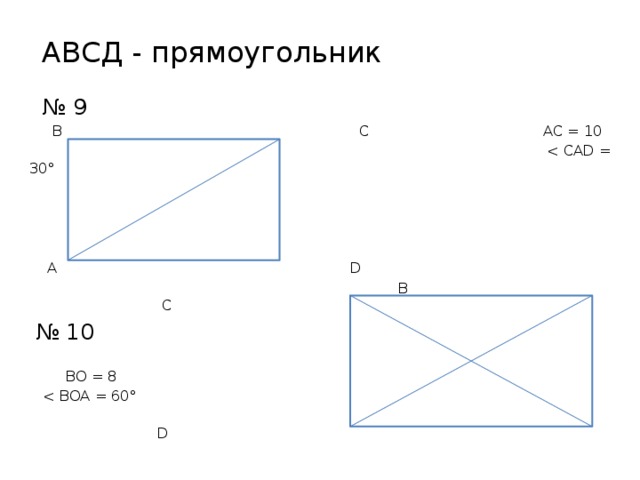
АВСД - прямоугольник

№ 9

В С АС = 10

А D

В С

№ 10

ВО = 8

А D

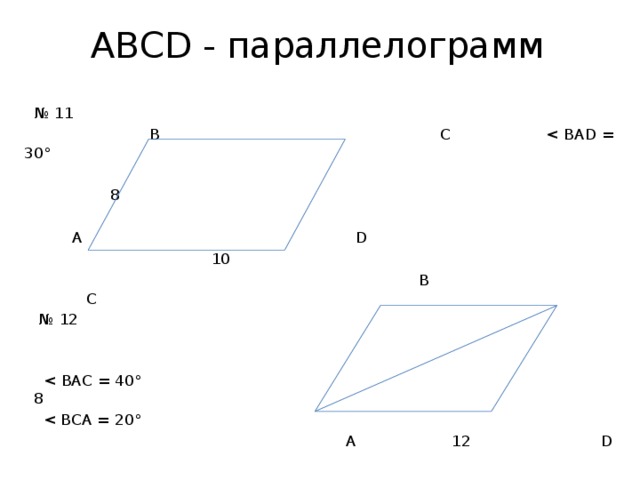
АВСD - параллелограмм

№ 11

В С

8

А D

10

В С

№ 12

А 12 D

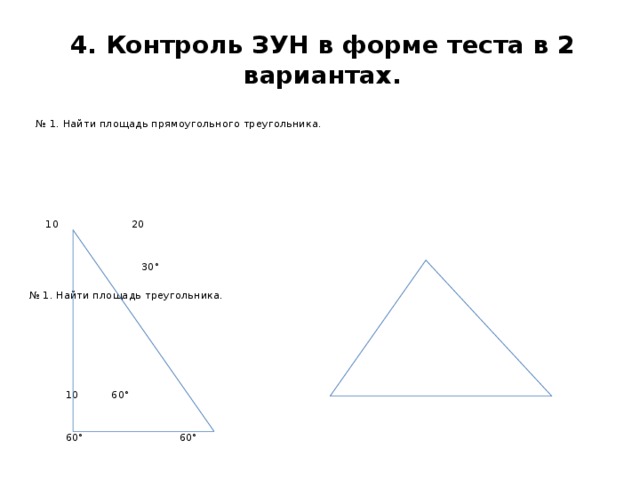
4. Контроль ЗУН в форме теста в 2 вариантах.

№ 1. Найти площадь прямоугольного треугольника.

10 20

30°

№ 1. Найти площадь треугольника.

10 60°

60° 60°

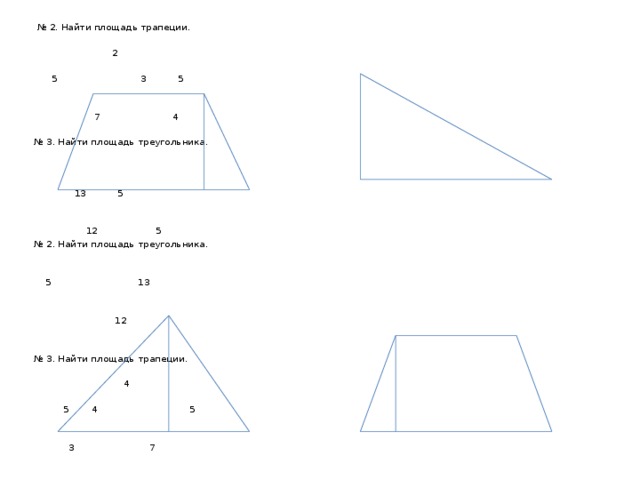
№ 2. Найти площадь трапеции.

2

5 3 5

7 4

№ 3. Найти площадь треугольника.

13 5

12 5

№ 2. Найти площадь треугольника.

5 13

12

№ 3. Найти площадь трапеции.

4

5 4 5

3 7

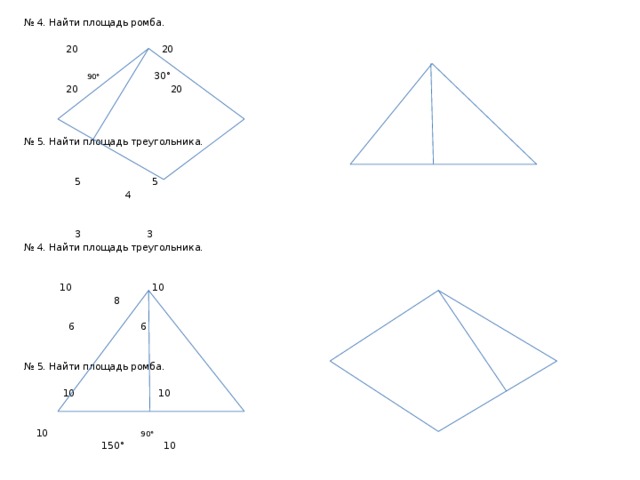
№ 4. Найти площадь ромба.

20 20

90° 30°

20 20

№ 5. Найти площадь треугольника.

5 5

4

3 3

№ 4. Найти площадь треугольника.

10 10

8

6 6

№ 5. Найти площадь ромба.

10 10

10 90°

150° 10

№ 6. В прямоугольной трапеции основания равны 17 см и 5 см, а большая боковая сторона 13 см. Найти площадь трапеции.

№ 7. Высоты параллелограмма 4 см и 5 см, а периметр равен 72 см. Найти площадь параллелограмма.

№ 6. В прямоугольной трапеции боковые стороны равны 15 см и 9 см, а большее основание 20 см. Найти площадь трапеции.

№ 7. Стороны параллелограмма равны 10 см и 14 см, а сумма высот к этим сторонам равна 12 см. Найти площадь параллелограмма.

Критерий оценки теста.

«5»-10 баллов

«4»-9,8,7 баллов

«3»-5,6 баллов

№ 1

1

№ 2

1

№ 3

№ 4

1

№ 5

1

№ 6

1

№ 7

2

3

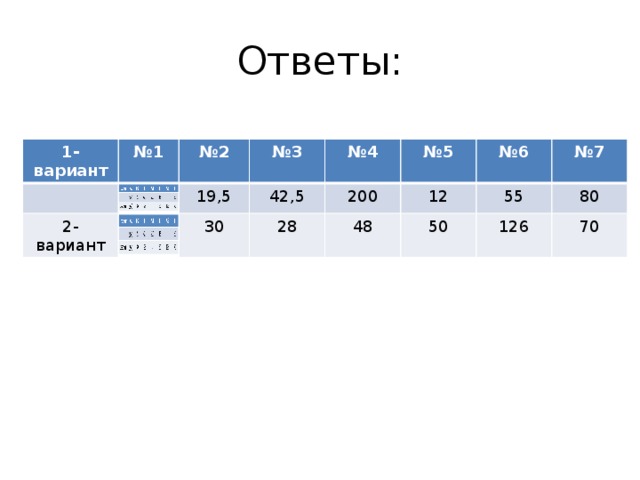
Ответы:

1-вариант

№ 1

№ 2

2-вариант

№ 3

19,5

42,5

№ 4

30

28

200

№ 5

12

№ 6

48

55

№ 7

50

80

126

70

5. Рефлексия.

6. Д/з Площадь круга и его частей, длина окружности и его дуги. Стр.

7. Исторические сведения.

В геометрии вавилоняне знали о таких соотношениях, например, как пропорциональность соответствующих сторон подобных треугольников. Им была известна теорема Пифагора и то, что угол, вписанный в полуокружность – прямой. Они располагали также правилами вычисления площадей простых плоских фигур, в том числе правильных многоугольников, и объемов простых тел. Число  Пи  вавилоняне считали равным 3.

Египет.  Наше знание древнеегипетской математики основано главным образом на двух папирусах, датируемых примерно 1700 до н.э. Излагаемые в этих папирусах математические сведения восходят к еще более раннему периоду – ок. 3500 до н.э. Египтяне использовали математику, чтобы вычислять вес тел, площади посевов и объемы зернохранилищ, размеры податей и количество камней, требуемое для возведения тех или иных сооружений. Но главной областью применения математики была астрономия, точнее расчеты, связанные с календарем.

Геометрия у египтян сводилась к вычислениям площадей прямоугольников, треугольников, трапеций, круга, а также формулам вычисления объемов некоторых тел. Надо сказать, что математика, которую египтяне использовали при строительстве пирамид, была простой и примитивной.

Классическая Греция.  С точки зрения 20 в. родоначальниками математики явились греки классического периода (6–4 вв. до н.э.). Математика, существовавшая в более ранний период, была набором эмпирических заключений. Напротив, в дедуктивном рассуждении новое утверждение выводится из принятых посылок способом, исключавшим возможность его неприятия.

Дедуктивный характер греческой математики полностью сформировался ко времени Платона и Аристотеля. Изобретение дедуктивной математики принято приписывать Фалесу Милетскому (ок. 640–546 до н.э.), который, как и многие древнегреческие математики классического периода, был также философом. Высказывалось предположение, что Фалес использовал дедукцию для доказательства некоторых результатов в геометрии, хотя это сомнительно.

Другим великим греком, с чьим именем связывают развитие математики, был Пифагор (ок. 585–500 до н.э.). Полагают, что он мог познакомиться с вавилонской и египетской математикой во время своих долгих странствий. Пифагор основал движение, расцвет которого приходится на период ок. 550–300 до н.э. Пифагорейцы создали чистую математику в форме теории чисел и геометрии. Целые числа они представляли в виде конфигураций из точек или камешков, классифицируя эти числа в соответствии с формой возникающих фигур («фигурные числа»). Слово «калькуляция» (расчет, вычисление) берет начало от греческого слова, означающего «камешек». Числа 3, 6, 10 и т.д. пифагорейцы называли треугольными, так как соответствующее число камешков можно расположить в виде треугольника, числа 4, 9, 16 и т.д. – квадратными, так как соответствующее число камешков можно расположить в виде квадрата, и т.д.

Рассматривая прямоугольный треугольник с единичными катетами, пифагорейцы обнаружили, что длина его гипотенузы равна , и это повергло их в смятение, ибо они тщетно пытались представить число в виде отношения двух целых чисел, что было крайне важно для их философии. Величины, непредставимые в виде отношения целых чисел, пифагорейцы назвали несоизмеримыми; современный термин – «иррациональные числа». Около 300 до н.э. Евклид доказал, что число несоизмеримо. Пифагорейцы имели дело с иррациональными числами, представляя все величины геометрическими образами. Если 1 и считать длинами некоторых отрезков, то различие между рациональными и иррациональными числами сглаживается. Произведение чисел  и есть площадь прямоугольника со сторонами длиной  и .Мы и сегодня иногда говорим о числе 25 как о квадрате 5, а о числе 27 – как о кубе 3. Именно пифагорейцам мы во многом обязаны той математикой, которая затем была систематизированно изложена и доказана в Началах Евклида. Есть основания полагать, что именно они открыли то, что ныне известно как теоремы о треугольниках, параллельных прямых, многоугольниках, окружностях, сферах и правильных многогранниках.

Одним из самых выдающихся пифагорейцев был Платон (ок. 427–347 до н.э.). Платон был убежден, что физический мир постижим лишь посредством математики. Считается, что именно ему принадлежит заслуга изобретения аналитического метода доказательства. (Аналитический метод начинается с утверждения, которое требуется доказать, и затем из него последовательно выводятся следствия до тех пор, пока не будет достигнут какой-нибудь известный факт; доказательство получается с помощью обратной процедуры.) Принято считать, что последователи Платона изобрели метод доказательства, получивший название «доказательство от противного». Заметное место в истории математики занимает Аристотель, ученик Платона. Аристотель заложил основы науки логики и высказал ряд идей относительно определений, аксиом, бесконечности и возможности геометрических построений. Около 300 до н.э. результаты многих греческих математиков были сведены в единое целое Евклидом, написавшим математический шедевр Начала.

Из немногих проницательно отобранных аксиом Евклид вывел около 500 теорем, охвативших все наиболее важные результаты классического периода. Свое сочинение Евклид начал с определения таких терминов, как прямая, угол и окружность. Затем он сформулировал десять самоочевидных истин, таких, как «целое больше любой из частей». И из этих десяти аксиом Евклид смог вывести все теоремы. Для математиков текст Начал Евклида долгое время служил образцом строгости, пока в 19 в. не обнаружилось, что в нем имеются серьезные недостатки, такие как неосознанное использование несформулированных в явном виде допущений. Упадок Греции.  После завоевания Египта римлянами в 31 до н.э. великая греческая александрийская цивилизация пришла в упадок. Цицерон с гордостью утверждал, что в отличие от греков римляне не мечтатели, а потому применяют свои математические знания на практике, извлекая из них реальную пользу. Однако в развитие самой математики вклад римлян был незначителен. Римская система счисления основывалась на громоздких обозначениях чисел. Главной ее особенностью был аддитивный принцип. Даже вычитательный принцип, например, запись числа 9 в виде IX, вошел в широкое употребление только после изобретения наборных литер в 15 в. Римские обозначения чисел применялись в некоторых европейских школах примерно до 1600, а в бухгалтерии и столетием позже.

Преемниками греков в истории математики стали индийцы. Индийские математики не занимались доказательствами, но они ввели оригинальные понятия и ряд эффективных методов. Именно они впервые ввели нуль и как кардинальное число, и как символ отсутствия единиц в соответствующем разряде. Махавира (850 н.э.) установил правила операций с нулем, полагая, однако, что деление числа на нуль оставляет число неизменным. Правильный ответ для случая деления числа на нуль был дан Бхаскарой (р. в 1114), ему же принадлежат правила действий над иррациональными числами. Индийцы ввели понятие отрицательных чисел (для обозначения долгов). Самое раннее их использование мы находим у Брахмагупты (ок. 630). Ариабхата (р. 476) пошел дальше Диофанта в использовании непрерывных дробей при решении неопределенных уравнений.

Наша современная система счисления, основанная на позиционном принципе записи чисел и нуля как кардинального числа и использовании обозначения пустого разряда, называется индо-арабской. На стене храма, построенного в Индии ок. 250 до н.э., обнаружено несколько цифр, напоминающих по своим очертаниям наши современные цифры.

Около 800 индийская математика достигла Багдада. Термин «алгебра» происходит от начала названия книги Аль-джебр ва-л-мукабала (Восполнение и противопоставление), написанной в 830 астрономом и математиком аль-Хорезми. В своем сочинении он воздавал должное заслугам индийской математики. Алгебра аль-Хорезми была основана на трудах Брахмагупты, но в ней явственно различимы вавилонское и греческое влияния. Другой выдающийся арабский математик Ибн аль-Хайсам (ок. 965–1039) разработал способ получения алгебраических решений квадратных и кубических уравнений. Арабские математики, в их числе и Омар Хайям, умели решать некоторые кубические уравнения с помощью геометрических методов, используя конические сечения. Арабские астрономы ввели в тригонометрию понятие тангенса и котангенса. Насирэддин Туси (1201–1274) в Трактате о полном четырехугольнике систематически изложил плоскую и сферическую геометрии и первым рассмотрел тригонометрию отдельно от астрономии.

И все же самым важным вкладом арабов в математику стали их переводы и комментарии к великим творениям греков. Европа познакомилась с этими работами после завоевания арабами Северной Африки и Испании, а позднее труды греков были переведены на латынь.

Спасибо за внимание!