Открытый урок на тему:
«Квадратный корень из произведения и дроби».
Цель:
-познакомиться с квадратным корнем из произведения и дроби.
Задачи:
- Вывести свойства квадратного корня из произведения и дроби;
- научиться применять их к нахождению значения выражений;
-развивать вычислительные навыки и логическое мышление.
Тип урока: урок ознакомления с новым материалом.
Структура урока.
Организационный момент.
Актуализация опорных знаний
Ознакомление с новой темой.
Закрепление.
Проверочная самостоятельная контрольная работа.
Творческое задание.
Домашнее задание.
Итог урока.
Ход урока
Организационный момент.
Актуализация опорных знаний:
А) Фронтальный опрос:
-что называется арифметическим квадратным корнем из числа а?
-какими свойствами обладает квадратный корень из числа а?
-в зависимости от числа а, сколько корней имеет уравнение х2=а?
Б) Устная работа.
1. Решите уравнение:
а) х2 = 16; б) х2 = 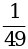 ; в) х2 = 0; г) х2 =
; в) х2 = 0; г) х2 = 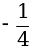 ; д) х2 = 10; е) х2 =
; д) х2 = 10; е) х2 = 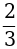 .
.
2. Вычислите:
а) 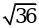 ; б)
; б) 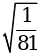 ; в)
; в) 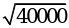 ; г)
; г) 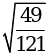 ; д)
; д) 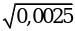 ; е)
; е) 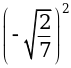 .
.
3. Изучение новой темы.
А) Объяснение:
Верно ли?
а) 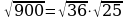 ; б)
; б)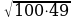
 =
= 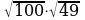 ;
;
Обратим внимание на второе равенство.
Что представляет левая часть равенства? (квадратный корень из произведения)
Что представляет правая часть равенства? (произведение квадратных корней)
Для всех ли случаев это утверждение будет верным?......
Мы выдвинули гипотезу: корень из произведения неотрицательных множителей равен произведению корней из этих множителей.
Сформулируйте это равенство.- Если a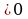 ; b
; b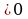 , то
, то 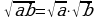
Давайте докажем его.
Дано: доказательство:
a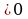 ; b
; b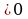 1.a
1.a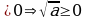
Доказать: b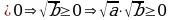
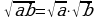 2.
2.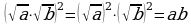
(здесь надо проговорить, что надо доказать)
-Будет ли это свойство распространяться на случай, когда число множителей под знаком корня больше двух? (да)
Давайте это запишем 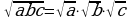 ; где
; где 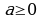 ;
; 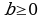 ;
; 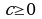
Устно.
Верно ли? а)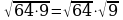 ; (да) б)
; (да) б) 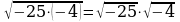 (нет)
(нет)
Докажите, что а)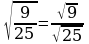 б)
б) 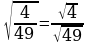
Для всех ли случаев это будет верным? (нет)
Как записать это равенство в общем виде?
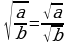 при
при 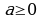 и b0.
и b0.
-Каков будет алгоритм доказательства? (доказывается аналогично).
Можно ли применить это свойство для 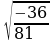 ;
; 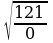 ;
; 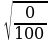 ?
?
А сейчас давайте закрепим применение этих свойств на примерах.
Устно: вычислите
а) ; б)
; б)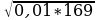 ; в)
; в)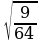 ; г)
; г) 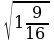 ; д)
; д)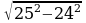 ; е)
; е) 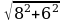 .
.
ж)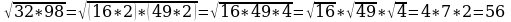
4. Закрепление темы.
№ 357, №358
5. Проверочная самостоятельная работа.
Тестовая работа.
| 1) Вычислите 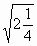 1) 3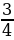 2) 1,4 3) 1 2) 1,4 3) 1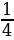 4) 1,5 4) 1,5 | 2) Решите уравнение 0,5у 2 = 8. 1) 2; -2
2) 2
3) 4; -4
4) 4
|
| 3) Найдите значение у, при котором - 2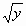 = 0. = 0. 1) 2,5
2) 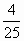 3) 3) 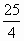 4) - 4) -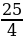
| Применив свойства арифметического квадратного корня, вычислите 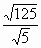 . .
1) 5; -5 2) 25 3) 5 4) 25; - 25
|
Вычислите 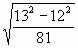 без помощи микрокалькулятора без помощи микрокалькулятора 1)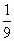 ;- ;- 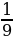 2) 2) 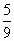 3) 3) 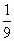 4) 4) 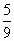 ; - ; -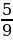 | 6) Даны числа: 0, (7); 1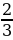 ; ; 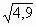 ; ; 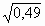 . Сколько среди них рациональных? . Сколько среди них рациональных?
1) 1 2) 2 3) 3 4) 4
|
| Ответы: 1) 4; 2) 3; 3) 3; 4)3; 5)2; 6)3
|
Самопроверка. Работа над ошибками.
6. Творческое задание
А) “Смотри, не ошибись!”
Определить неизвестный множитель:
а)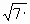 ? = 7; б) (а -
? = 7; б) (а - 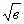 ) * (?) = а 2 – в; в)
) * (?) = а 2 – в; в)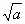 * ? = а; г) (
* ? = а; г) (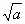 +
+ 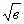 ) * (?) = а – в;
) * (?) = а – в;
д)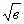 *? = в.
*? = в.
Б) Задание “Проверь, не пользуясь микрокалькулятором ”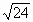
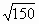
В) Резервное задание для обеспечения занятости и развития наиболее подготовленных учащихся.
Решить уравнение: 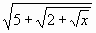 = 3.
= 3.
7. Домашнее задание: п.15, № 359 , 361
8. Подведение итогов.
Выставление оценок учащимся.
Какие формулы мы повторили на уроке?
Что вам понравилось на уроке?
Что бы вы хотели выполнить еще раз?
Обращаюсь к классу: « Прошу продолжить мою фразу «Знания, полученные на этом уроке, мне необходимы для того, чтобы …»».
Тестовая работа.
| 1) Вычислите 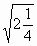 1) 3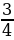 2) 1,4 3) 1 2) 1,4 3) 1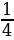 4) 1,5 4) 1,5 | 2) Решите уравнение 0,5у 2 = 8. 1) 2; -2
2) 2
3) 4; -4
4) 4
|
| 3) Найдите значение у, при котором - 2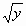 = 0. = 0. 1) 2,5
2) 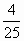 3) 3) 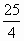 4) - 4) -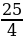
| Применив свойства арифметического квадратного корня, вычислите 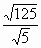 . .
1) 5; -5 2) 25 3) 5 4) 25; - 25
|
Вычислите 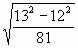 без помощи микрокалькулятора без помощи микрокалькулятора 1)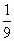 ;- ;- 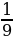 2) 2) 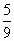 3) 3) 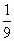 4) 4) 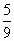 ; - ; -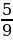 | 6) Даны числа: 0, (7); 1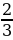 ; ; 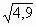 ; ; 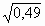 . Сколько среди них рациональных? . Сколько среди них рациональных?
1) 1 2) 2 3) 3 4) 4
|
Тестовая работа.
| 1) Вычислите 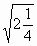 1) 3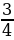 2) 1,4 3) 1 2) 1,4 3) 1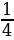 4) 1,5 4) 1,5 | 2) Решите уравнение 0,5у 2 = 8. 1) 2; -2
2) 2
3) 4; -4
4) 4
|
| 3) Найдите значение у, при котором - 2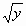 = 0. = 0. 1) 2,5
2) 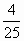 3) 3) 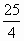 4) - 4) -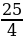
| Применив свойства арифметического квадратного корня, вычислите 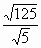 . .
1) 5; -5 2) 25 3) 5 4) 25; - 25
|
Вычислите 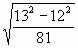 без помощи микрокалькулятора без помощи микрокалькулятора 1)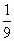 ;- ;- 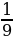 2) 2) 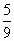 3) 3) 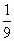 4) 4) 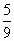 ; - ; -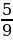 | 6) Даны числа: 0, (7); 1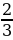 ; ; 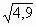 ; ; 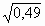 . Сколько среди них рациональных? . Сколько среди них рациональных?
1) 1 2) 2 3) 3 4) 4
|







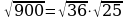 ; б)
; б)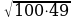
 =
= 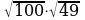 ;
;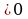 ; b
; b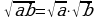
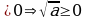
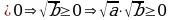
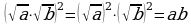
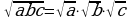 ; где
; где 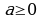 ;
; 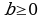 ;
; 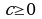
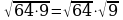 ; (да) б)
; (да) б) 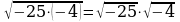 (нет)
(нет)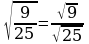 б)
б) 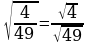
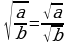 при
при 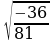 ;
; 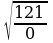 ;
; 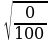 ?
? ; б)
; б)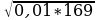 ; в)
; в)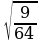 ; г)
; г) 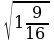 ; д)
; д)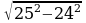 ; е)
; е) 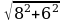 .
.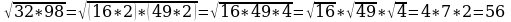
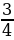 2) 1,4 3) 1
2) 1,4 3) 1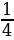 4) 1,5
4) 1,5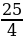
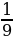 2)
2) 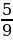
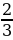 ;
; 









