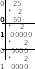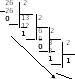Урок. Перевод чисел в позиционных системах счисления.
Цели: расширение знаний учащихся о системах счисления.
Задачи:
обучающие:формирование и отработка навыков перевода чисел между позиционными системами счисления;
развивающие:развитие логического мышления учащихся;
воспитательные: воспитание интереса к историческим сведениям, формирование ИКТ грамотности учащихся.
УУД
Регулятивные: Определять цель учебной деятельности самостоятельно и с помощью учителя, искать средства ее осуществления;планировать, т.е. составлять план действий с учетом конечного результата.
Коммуникативные: Умениеполноиточновыражатьсвоимысливсоответствиисзадачамииусловиямикоммуникации, владениемонологическойидиалогическойформамиречи.
Познавательные:Умение анализировать, выделять и формулировать задачу; умение осознанно строить речевое высказывание;Самостоятельноесозданиеспособоврешенияпроблемтворческогоипоисковогохарактера.
Личностные: осознание своих возможностей.
Методы обучения: изучения и первичного закрепления новых знаний и способов деятельности.
Материально – техническое оснащение: персональный компьютер учителя, проектор, экран.
ХОД УРОКА:
Организационный момент
Постановка целей и задач урока
Повторение материала;
Изучение нового материала
Закрепление материала
Организация работы на дом
Ей было тысяча сто лет,
Она в сто первый класс ходила,
В портфеле по сто книг носила.
Все это правда, а не бред.
Когда, пыля десятком ног,
Она шагала по дороге,
За ней всегда бежал щенок
С одним хвостом, зато стоногий.
Она ловила каждый звук
Своими десятью ушами,
И десять загорелых рук
Портфель и поводок держали.
И десять темно-синих глаз
Рассматривали мир привычно...
Но станет все совсем обычным,
Когда поймете наш рассказ.
Ребята, что необычного в этом стихотворении?
Чем бы вы объяснить странные противоречия в числах этого стихотворения?
Как узнать, сколько лет было девочке, и в какой класс она ходила?
Мы с вами уже говорили, что одно и то же количество объектов можно обозначить по-разному (разными наборами цифр). От чего это зависит?
Сообщение темы, цели и задач.
Тему «Системы счисления» мы изучаем не первый урок. На уроке мы с вами повторим основные понятия по данной теме, проверим свои знания, поработаем с переводом чисел из одной позиционной системы счисления в другую.
Ребята, а теперь определите для себя цель сегодняшнего урока. Закрепить умение переводить числа из одной системы счисления в другую.
Давайте немного поиграем и вспомним основные понятия с помощью «Лото». Давайте вместе определим правила игры: выбираем номер вопроса, даем друг другу ответить, не перебиваем, если отвечающий затрудняется, помогаем ему. Можно пользоваться тетрадями.
| Уровень I | Уровень II |
| Что мы используем для кодирования числовой информации (для обозначения чисел)? | Что такое кодирование информации? |
| Какой СС мы с вами пользуемся? | Давайте вспомним, что такое система счисления? |
| Найдите ошибку в записи: 8438 | Что такое основание системы счисления? |
| Алфавит какой системы счисления представлен: 0,1,2,3,4,5,6,7? | Что такое алфавит системы счисления? |
| Автор стихотворения «Необыкновенная девочка» допустил неточность в названии двоичных кодов. В чем она? | Какой системой счисления пользуется для кодирования числовой информации компьютер и почему? |
| Какая система счисления была первой? | Какое минимальное основание должна иметь система счисления, если в ней могут быть записаны числа: 10, 21, 201, 1201? |
Актуализация знаний.
1.В каком виде представлена числовая информация в памяти компьютера?
2. Как перевести число из десятичной системы счисления в любую другую?
Объяснение нового материала.
Перевод чисел в десятичную систему счисления.
Правило:Для того чтобы число из любой системы счисления перевести в десятичную систему счисления, необходимо его представить в развернутом виде и произвести вычисления.
Пример1. Перевести число 1101102 из двоичной системы счисления в десятичную.
Решение:
5 4 3 2 1 0
1 1 0 1 1 0 2 = 1*25 + 1*24 + 0*23+1*22+1*21+0*20 = =32+16+4+2=5410
Ответ: 1101102 = 5410
Пример2. Перевести число 101,012 из двоичной системы счисления в десятичную.
Решение:
2 1 0 -1 -2
1 0 1, 0 1 2 = 1*22 + 0*21 + 1*20+0*2-1+1*2-2 =4+0+1+0+0,25=5,2510
Ответ: 101,012 = 5,2510
Пример3. Перевести число 234,68 из восьмеричной системы в десятичную:
Решение:
2 1 0 -1
2 3 4, 68 = 2*82 +3*81 + 4*80 +6*8-1= 2*64+3*8+4+6*0,125= 128+24+4+0,75 =156,7510
Ответ: 234,68 = 156,7510.
Пример4. Перевести число 2Е16 в десятичную систему счисления.
Решение:
1 0
2 Е16 = 2*161 +14*160 = 32 +14 = 4610.
Ответ: 2Е16 = 4610.
Самостоятельно:
Перевести из различных систем счисления в десятичную:
а) 1111001112 г) 367,28
б) 1001110,112 в) АВ2Е,816
Перевод чисел из десятичной системы счисления в другую.
Правилоперевода целых чисел из десятичной системы счисления в систему с основанием q:
Последовательно выполнять деление исходного числа и получаемых частных на q до тех пор, пока не получим частное, меньшее делителя.
Полученные при таком делении остатки – цифры числа в системе счисления q – записать в обратном порядке (снизу вверх).
П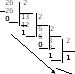 ример1. Перевести 2610 в двоичную систему счисления. А10→А2
ример1. Перевести 2610 в двоичную систему счисления. А10→А2
Решение:
Ответ: 2610=110102
Перевод дробных чисел из десятичной системы счисления в другую.
Правилоперевода дробных чисел из десятичной системы счисления в систему с основанием q:
Последовательно выполнять умножение исходного числа и получаемых дробные части на q до тех пор, пока дробная часть не станет равна нулю или не достигнем требуемую точность.
Полученные при таком умножении целые части - числа в системе счисления q – записать в прямом порядке (сверху вниз).
Пример. Перевести 0,562510 в двоичную систему счисления. А10→А2
Р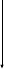
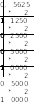 ешение:
ешение:
Ответ: 0,562510=0,10012
Примечание:Процесс умножения может продолжаться до бесконечности. Тогда его прерывают на некотором шаге, когда считают, что получена требуемая точность представления числа
Перевод произвольных чисел из десятичной системы счисления в другую.
Перевод произвольных чисел, то есть чисел, содержащих целую и дробную части, осуществляют в два этапа. Отдельно переводится целая часть, отдельно – дробная. В итоговой записи полученного числа целая часть отделяется от дробной запятой.
Пример1. Перевести 26,2510 в двоичную систему счисления. А10→А2
Решение:
переводим целую часть переводим дробную часть
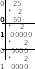
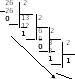
Ответ: 26,2510=11010,012
Самостоятельно:
Перевести из десятичной системы счисления следующие числа:
а) 17310→А2
б) 40410→А16
в) 12510→А8
Домашнее задание: Выучить конспект.
Выполнить следующие задания:
Переведите двоичные числа в десятичную систему счисления: 101011011; 100010,011101; 0,000110101
Переведите десятичные числа в двоичную, восьмеричную и шестнадцатеричную систему счисления: 87; 321; 235.






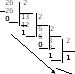 ример1. Перевести 2610 в двоичную систему счисления. А10→А2
ример1. Перевести 2610 в двоичную систему счисления. А10→А2
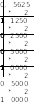 ешение:
ешение: