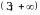Государственное автономное общеобразовательное учреждение
Чукотского автономного округа «Чукотский окружной профильный лицей»
Разработка урока по математике:
Множество значений функции.
Ершова Марина Ивановна
учитель математики
г. Анадырь, 2024 год
Урок обобщающего повторения при подготовке к ЕГЭ. 10 класс.
Тема: Множество значений функции. (2ч)
Цель: Обобщить и систематизировать знания по теме «Множество значений функции»
Научить находить множество значений элементарных функций
Развивать представления о функциях по их графикам.
Ход урока:
1.Организационный момент
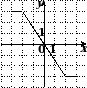
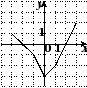
2.Нахождение множества значений функции по графикам
3.Обобщение теоретического материала
4.Решение задач
5.Тесты
6.Домашнее задание
Учитель: На сегодняшнем уроке мы будем рассматривать множество значений элементарных функций, будем находить множество значений функций по графику, а также выполним тестовые задания по подготовке к ЕГЭ.
Учитель: Обратите внимание на экран, на каждом слайде изображен график функции, найдём их множество значений.
Объяснение учителя:
Множеством (областью) значений Е(у) функции у = f(x) называется множество всех таких чисел y0 , для каждого из которых найдется число x0 такое, что: f(x0) = y0·
Напомним области значений основных элементарных функций.
Областью значений всякого многочлена четной степени является промежуток [т,+ 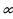 ), где т - наименьшее значение этого многочлена, либо промежуток (-
), где т - наименьшее значение этого многочлена, либо промежуток (-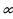 , n], где n - наибольшее значение этого многочлена.
, n], где n - наибольшее значение этого многочлена.
Областью значений всякого многочлена нечетной степени является R.
Е  ) = (
) = (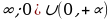
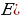 )=[0, +
)=[0, +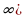
Е( 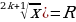 E (
E (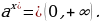
Е (loga х) =R E (sin x) = E(cos x)= [-1,1]
Е (arcsin x) = [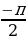 ,
,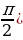 E (arсcos x)= [0
E (arсcos x)= [0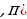
Е (tg x) = E(ctg x)=R E(arctg x)= (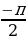 ,
,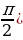
Е (arcctg x ) = (0,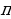 ).
).
Отметим, что задания на нахождение множества значений какой-то функции решаются преимущественно двумя методами: аналитическим и алгебраическим.
Приведем одно замечание. Предположим, что функция f(x) является сложной функцией, в которой можно выделить "подфункцию" t = t(x). Тогда y = f(t) = f(t(x)). Отметим, что неважно, какой является функция t = t(x) (возрастающей, возрастающе-убывающей и т.д.). Если нам известна ее область значений E(t), то при нахождении области значений функции У = f(t) = f(t(x)) целесообразно считать, что t возрастает на E(t) как какой-то новый аргумент.
В соответствии с этим функцию У = f(t) целесообразно считать такой, каковой она является от аргумента t на промежутке E(t). Например, пусть нам дана функция y=2cos x. Вводим новую переменную t(x) = cos x.
Понятно, что E(t) = [-1, 1]. Тогда функцию y(t) = 2t + 1 целесообразно считать линейной на промежутке [-1, 1]. Это никак не повлияет на нахождение Е(у), но напротив, облегчит нам эту процедуру.
Находим Е(у). Функция y(t) = 2t + 1 на промежутке [-1,1] является линейной и возрастающей, потому Е(у) = [2(-1) + 1,2·1 + 1] = [-1,3].
Пример 1. Найдите область значения функции у=3+cos x
[0;3]; 2) [-4;2]; 3) [-4;0] 4) [2;4];
Решение: Значения косинуса составляют промежуток [-1;1], значит, -1+3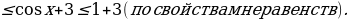 Получим Е(у)= [2;4]
Получим Е(у)= [2;4]
Номер ответа: 4.
Пример 2. Найдите область значения функции у=2-si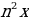
[1;2] 2) [1;3] 3)[0;3] 4) [0;1.]
Решение: Так как -1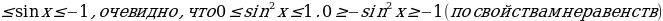 . Прибавив ко всем частям двойного неравенства 2, получим 2
. Прибавив ко всем частям двойного неравенства 2, получим 2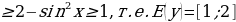
Номер ответа: 1
Пример 3. Найдите множество значений функции у=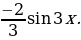
[-2;2] 2) [-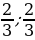 ] 3) [-0,5; 1;5] 4) [-1
] 3) [-0,5; 1;5] 4) [-1 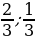 ]
]
Решение: -1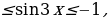 умножим все части неравенства на число (
умножим все части неравенства на число (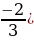 .
.
При этом знак неравенства меняется на противоположный 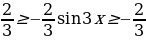 или
или
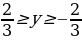 .
.
Е(у)= [-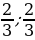 ]
]
Номер верного ответа: 2.
Пример 4.
Найдите наибольшее целое значение функции.
y=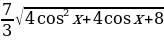
Решение: Запишем функцию в виде y=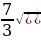 или y=
или y=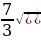
Учтём ограниченность функции косинус -2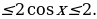 Ко всем частям неравенства прибавим число 1 и получим:
Ко всем частям неравенства прибавим число 1 и получим:
-1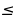 2 cos x+1
2 cos x+1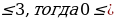 2cos x+1
2cos x+1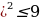 . Ко всем частям неравенства прибавим число 7 и получим 7
. Ко всем частям неравенства прибавим число 7 и получим 7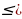 Умножим все части неравенства на положительное число
Умножим все части неравенства на положительное число 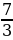 и получим
и получим 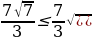 .
.
Учтём, что 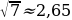 и
и 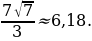 Тогда имеем: 6,18
Тогда имеем: 6,18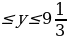 , наибольшее целое значение, лежащее в этом промежутке, 9.
, наибольшее целое значение, лежащее в этом промежутке, 9.
Ответ:9.
Пример 5. Найдите наибольшее целое значение функции.
y= 13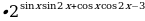
Решение: Используя формулу для косинуса разности двух углов, получим y= 13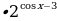 . Учтём ограниченность функции косинус: -1
. Учтём ограниченность функции косинус: -1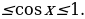 Из всех частей этого неравенства вычтем число 3 и получим: -4
Из всех частей этого неравенства вычтем число 3 и получим: -4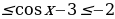 . Показательная функция с основанием 2 (большим единицы) является возрастающей. Поэтому получаем:
. Показательная функция с основанием 2 (большим единицы) является возрастающей. Поэтому получаем: 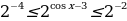 или
или 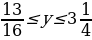 . Наибольшее целое значение, лежащее в этом промежутке, у=3.
. Наибольшее целое значение, лежащее в этом промежутке, у=3.
Ответ: 3.
Пример 6. Найти множество значений функции у=tg x-3, учитывая множество значений функции тангенс получим неравенство 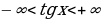 , вычитая из обеих частей неравенства 3 получим промежуток (
, вычитая из обеих частей неравенства 3 получим промежуток (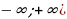
Ответ:(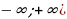
Пример 7. Найти множество значений функции у=tg2 x+5, учитывая множество значений функции тангенс получим неравенство 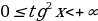 , прибавляя к обеим частям неравенства 5, получим [5;+
, прибавляя к обеим частям неравенства 5, получим [5;+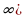
Ответ: [5;+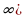
Пример 8. Найти множество значений функции у=2сtg x-3, учитывая множество значений функции котангенс получим неравенство 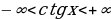 , умножив обе части неравенства на 2 получим неравенство
, умножив обе части неравенства на 2 получим неравенство 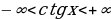 , вычитая из обеих частей неравенства 3 получим промежуток (
, вычитая из обеих частей неравенства 3 получим промежуток (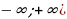
Ответ:(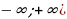
Пример 9. . Найти множество значений функции у=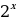 +3, учитывая множество значений функции у=
+3, учитывая множество значений функции у=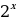 получим неравенство
получим неравенство 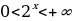 , прибавляя к обеим частям неравенства 3, получим промежуток (3;
, прибавляя к обеим частям неравенства 3, получим промежуток (3;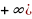
Ответ: (3;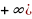
Пример 10. Укажите наибольшее целое число, входящее в множество значений функции у=4- 0,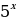 , учитывая множество значений функции у=0,
, учитывая множество значений функции у=0,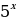 , получим неравенство
, получим неравенство
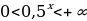 ,умножив обе части неравенства на -1, получим
,умножив обе части неравенства на -1, получим 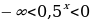 , прибавляя к обеим частям неравенства число 4, получим промежуток (-
, прибавляя к обеим частям неравенства число 4, получим промежуток (-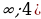 , таким образом наибольшее целое число, входящее в множество значений 3.
, таким образом наибольшее целое число, входящее в множество значений 3.
Ответ: 3.
Пример 11. Найдите наименьшее значение функции
g(x)=log3(16-х2) на промежутке [0;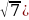
Замечание: Можно заметить, что на промежутке [0;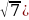 функция у=16-х2 убывает, т.е.
функция у=16-х2 убывает, т.е.
у(0)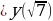
Функция g(t)=log3 t возрастает на всей области определения. Значит, наименьшее значение на промежутке [0;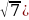 функция g(x)=log3(16-х2) принимает в точке х0 =
функция g(x)=log3(16-х2) принимает в точке х0 =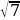
Решение: g(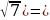 log3(16-
log3(16-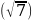 2
2 = log3(16-
= log3(16-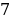 )= log3 9=2
)= log3 9=2
Ответ: 2.
Пример 12. Найти наименьшее значение функции g(x)=log0,5(4-х2)
Ответ: -2
Решение задач у доски.
1.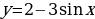
2.y = sin x -5
3.y= 1- 2 sin x
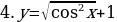
5.y= cos x-2
6.y= 2 sin x+3
7.y=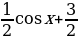
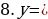
9.y= 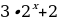
10.y=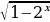
11.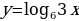
12. y=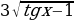
Ответы:
1.[-1; 5]
2.[-6;-4]
3.[-1;3]
4. [1;2]
5. [-1;-3]
6. [1;5]
7. [1;2]
8. (-4;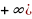
9. (2;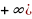
10.[0;1)
11.(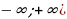
12.[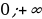 )
)
Задачи для самостоятельного решения повышенного уровня.
1.Найдите наименьшее целое значение функции y = 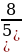
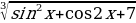
2. Найдите наименьшее целое значение функции у = 3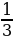
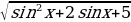
3.Найдите наибольшее целое значение функции у=25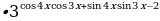
4. Найдите наименьшее целое значение функции
у=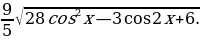
5. Найдите наименьшее значение функции
y = log0,5(2-x2).
6. Найдите наименьшее значение функции
y = log0,5(4-x2).
7. Найдите наименьшее значение функции
g(x) = log0,5(8-x2).
8.Найдите наименьшее значение функции
g(x) = log0,5(0,125-x2).
Ответы:
3
7
8
7
-1
-2
-3
3
5.Решение тестовых заданий (3 уровня)
Предлагаются тесты с выбором ответа по типу ЕГЭ (рассчитанные на 15 минут), учитель сразу проверяет и оценивает работу учащихся.
Вариант 1.
1. Вычислите: 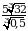 .
.
2. Упростите выражение 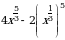 .
.
3. Найдите значение выражения 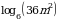 , если
, если 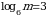 .
.
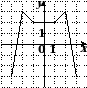
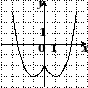
4. На рисунке изображен график функции 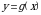 , определенной на промежутке
, определенной на промежутке 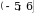 . Укажите все значения аргумента, при которых функция принимает неотрицательные значения.
. Укажите все значения аргумента, при которых функция принимает неотрицательные значения.
5. Укажите область определения функции 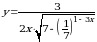 .
.
6. Укажите область значений функции 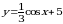 .
.
7. Решите неравенство 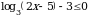 .
.
Вариант 2.
1. Упростите выражение 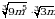 .
.
2. Вычислите: 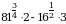 .
.
3. Вычислите: 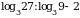 .
.
| 1) | 3 | 2) | – 0,5 | 3) | 0,5 | 4) | 8 |
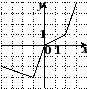
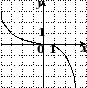
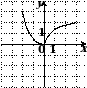
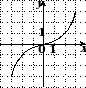
4. На одном из рисунков изображен график четной функции. Укажите этот рисунок.
5. Укажите область определения функции 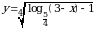 .
.
6. Укажите область значений функции 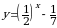 .
.
7. Решите неравенство 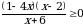 .
.
Вариант 3.
1. Вычислите: 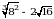 .
.
2. Упростите выражение 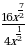 .
.
3. Вычислите: 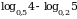 .
.
4. На одном из рисунков изображен график нечетной функции. Укажите этот рисунок.
5. Укажите область определения функции 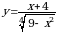 .
.
6. Укажите область значений функции 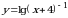 .
.
7. Решите неравенство 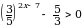 .
.
Ответы:
| № | Вариант 1 | Вариант 2 | Вариант 3 |
| 1 | 1 | 2 | 2 |
| 2 | 3 | 3 | 3 |
| 3 | 4 | 1 | 2 |
| 4 | 2 | 2 | 3 |
| 5 | 3 | 3 | 1 |
| 6 | 4 | 4 | 4 |
| 7 | 1 | 1 | 3 |
5 заданий – оценка 3, 6 заданий – 4, 7 заданий-5.
6. Домашнее задание ( в качестве домашнего задания предлагаются тесты 3-х уровней,)
7. Итоги урока.





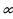 ), где т - наименьшее значение этого многочлена, либо промежуток (-
), где т - наименьшее значение этого многочлена, либо промежуток (- ) = (
) = (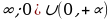
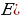 )=[0, +
)=[0, +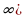
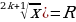 E (
E (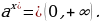
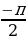 ,
,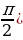 E (arсcos x)= [0
E (arсcos x)= [0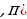
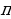 ).
). 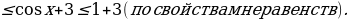 Получим Е(у)= [2;4]
Получим Е(у)= [2;4]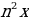
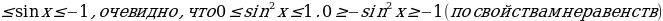 . Прибавив ко всем частям двойного неравенства 2, получим 2
. Прибавив ко всем частям двойного неравенства 2, получим 2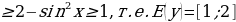
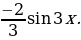
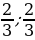 ] 3) [-0,5; 1;5] 4) [-1
] 3) [-0,5; 1;5] 4) [-1 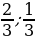 ]
]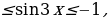 умножим все части неравенства на число (
умножим все части неравенства на число (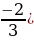 .
.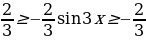 или
или 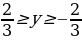 .
. 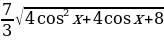
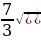 или y=
или y=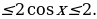 Ко всем частям неравенства прибавим число 1 и получим:
Ко всем частям неравенства прибавим число 1 и получим: 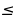 2 cos x+1
2 cos x+1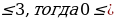 2cos x+1
2cos x+1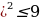 . Ко всем частям неравенства прибавим число 7 и получим 7
. Ко всем частям неравенства прибавим число 7 и получим 7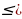 Умножим все части неравенства на положительное число
Умножим все части неравенства на положительное число 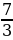 и получим
и получим 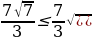 .
.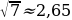 и
и 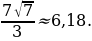 Тогда имеем: 6,18
Тогда имеем: 6,18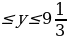 , наибольшее целое значение, лежащее в этом промежутке, 9.
, наибольшее целое значение, лежащее в этом промежутке, 9.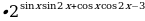
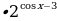 . Учтём ограниченность функции косинус: -1
. Учтём ограниченность функции косинус: -1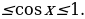 Из всех частей этого неравенства вычтем число 3 и получим: -4
Из всех частей этого неравенства вычтем число 3 и получим: -4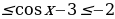 . Показательная функция с основанием 2 (большим единицы) является возрастающей. Поэтому получаем:
. Показательная функция с основанием 2 (большим единицы) является возрастающей. Поэтому получаем: 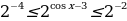 или
или 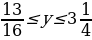 . Наибольшее целое значение, лежащее в этом промежутке, у=3.
. Наибольшее целое значение, лежащее в этом промежутке, у=3.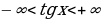 , вычитая из обеих частей неравенства 3 получим промежуток (
, вычитая из обеих частей неравенства 3 получим промежуток (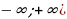
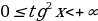 , прибавляя к обеим частям неравенства 5, получим [5;+
, прибавляя к обеим частям неравенства 5, получим [5;+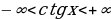 , умножив обе части неравенства на 2 получим неравенство
, умножив обе части неравенства на 2 получим неравенство 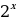 +3, учитывая множество значений функции у=
+3, учитывая множество значений функции у=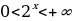 , прибавляя к обеим частям неравенства 3, получим промежуток (3;
, прибавляя к обеим частям неравенства 3, получим промежуток (3;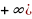
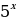 , учитывая множество значений функции у=0,
, учитывая множество значений функции у=0,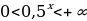 ,умножив обе части неравенства на -1, получим
,умножив обе части неравенства на -1, получим 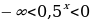 , прибавляя к обеим частям неравенства число 4, получим промежуток (-
, прибавляя к обеим частям неравенства число 4, получим промежуток (-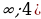 , таким образом наибольшее целое число, входящее в множество значений 3.
, таким образом наибольшее целое число, входящее в множество значений 3.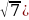
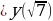
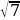
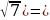 log3(16-
log3(16-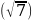 2
2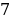 )= log3 9=2
)= log3 9=2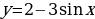
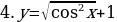
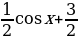
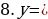
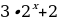
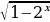
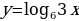
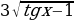
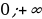 )
)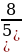
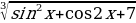
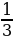
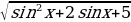
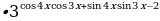
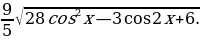
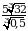 .
.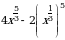 .
.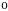
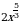
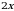
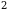
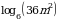 , если
, если 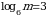 .
.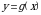 , определенной на промежутке
, определенной на промежутке  . Укажите все значения аргумента, при которых функция принимает неотрицательные значения.
. Укажите все значения аргумента, при которых функция принимает неотрицательные значения.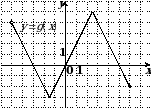
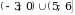
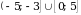
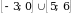
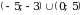
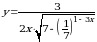 .
.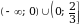
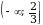
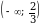
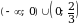
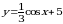 .
.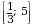
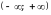
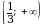
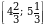
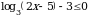 .
.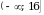
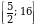
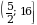
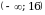
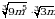 .
.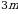
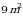
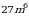
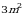
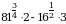 .
.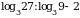 .
.
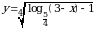 .
.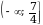
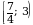
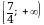
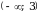
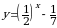 .
.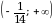
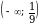
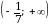
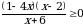 .
.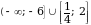
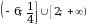
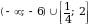
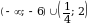
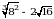 .
.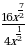 .
.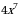
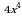
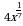
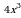
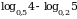 .
.
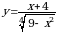 .
.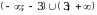
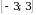
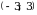
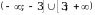
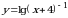 .
.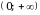
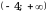
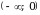
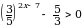 .
.