| Ход урока
Постановка цели, мотивация
В математике существует много высказываний, но это высказывание на сегодня близко для меня. В этом высказывании я убрала некоторые слова, и вы должны вставить слова которые как вам кажется больше всего должны сюда подойти, которые близки для вас на сегодня: «Математика существует не для того, чтобы навязывать кому-либо тяжелую работу. Наоборот, она существует только для удовольствия. Для удовольствия тех, кто любит анализировать то, что он делает, или может сделать, или то, что уже сделал в надежде сделать это еще лучше» (канадский поэт Роберт Бринсперт)
Вы от уроков математики получаете удовольствие? И когда? Какую тему мы будем сегодня с вами рассматривать? Можно ли от производной получить удовольствие? Сегодняшнее занятие мы посвятим решению задач на применение геометрического смысла производной, которые включены в задания на ЕГЭ. Вы должны научится проводить анализ условия задачи, выделять главный вопрос задачи, научится составлять алгоритм решения, конструировать способ решения на основе имеющихся знаний, выделять теоретические знания при решении задания. 2. Сформулируйте для себя цели которые бы вы хотели получить сегодня от урока Но, а для этого нам нужен фундамент. Давайте вспомним что вы знаете о производной На ваших столах лежат рабочие листы к данному уроку, которые по итогам урока должны стать для вас опорным конспектом.
Запишите сегодняшнее число, и заполните эти листы «Актуализация знаний» В пункте 1 «Актуализация знаний» на рабочем листе заполните пропуски и ответьте на вопросы. 1.1 1.1. что является касательной к графику функции прямая 1.2. запишите формулу которой задается прямая 1.3. что такое в формуле угловой коэффициент 1.4. если , то касательная расположена в I и II коорд. четвертях . если , то касательная расположена во II и IV коорд. четвертях если , то касательная параллельна или совпадает с ОХ . 1.5. продолжите равенство Проверка ответов. (по слайду) 4.Закрепление и расширение знаний (коллективная работа) Вначале на примере двух задач открытого банка заданий ЕГЭ мы разберем решение. Проанализируем условие задачи. Определим основные определения, формулы, которые нам нужны для их решения. Выделим главный вопрос, сконструируем способ их решения и запишем его в виде алгоритма.
Задача 1. На рисунке изображен график функции 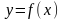 . Прямая, проходящая через начало координат, касается графика этой функции в точке с абсциссой 8. Найдите . Прямая, проходящая через начало координат, касается графика этой функции в точке с абсциссой 8. Найдите 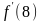 . . 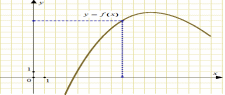 Что значит найти 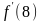 ? ? Какие понятия мы будем использовать, чтобы дать ответ на поставленный вопрос? Как по другому можно сформулировать вопрос задачи? Что для ответа на этот вопрос нужно знать? Какие дополнительные построения нужно выполнить? Какую фигуру нужно рассмотреть и почему? Что нужно найти? Итак, чему равно значение производной в точке касания? Способ решения: Провожу диагональ прямоугольника из начала отсчета– отрезок касательной, проходящей через точку касания и начало отсчета. Рассматриваю прямоугольный треугольник одним из углов которого является угол наклона касательной к оси Ох По геометрическому смыслу производной…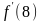 = =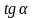 Из треугольника нахожу значение тангенса угла наклона касательной к оси Ох 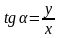 Задача 2. На рисунке изображён график функции 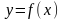 и касательная к нему в точке с абсциссой и касательная к нему в точке с абсциссой 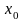 . Найдите значение производной функции . Найдите значение производной функции 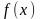 в точке в точке 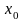 . . 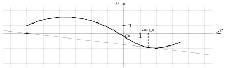
Что значит найти значение производной функции 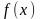 в точке в точке 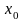 .? .? Какие понятия мы будем использовать, чтобы дать ответ на поставленный вопрос? Как по другому можно сформулировать вопрос задачи? Что для ответа на этот вопрос нужно знать? Какие дополнительные построения нужно выполнить? Какую фигуру нужно рассмотреть и почему? Что нужно найти? Итак, чему равно значение производной в точке 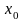 ? ? Способ решения: Достраиваю до прямоугольного треугольника с острым углом, равным углу наклона касательной к Ох. По геометрическому смыслу производной 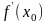 = =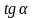 Нахожу тангенс угла наклона касательной к Ох: 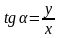
5.Закрепление и расширение знаний (самостоятельная групповая работа) Учитель выступает в роли координатора действий групп. Разбиваемся на 4 группы и решаем по одной задаче, используя приемы и рассуждения как в предыдущих задачах. Затем защищаете свой способ решения вашей задачи. Группа 1 Группа 2 | задача | решение | алгоритм решения | Замечания к решению | |
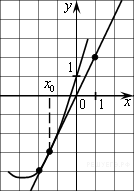 На рисунке изображён график функции y=f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.
|
|
|
| | задача | решение | Теоретические знания | Замечания к решению | |
Прямая 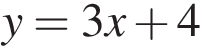 является касательной к графику функции является касательной к графику функции 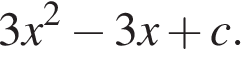 Найдите Найдите 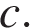
|
|
|
|
Группа 3 Группа 4
| задача | решение | Теоретические знания | Замечания к решению | | На рисунке изображён график функции y = f(x). Числа a, b, c, d и e задают на оси x четыре интервала. Пользуясь графиком, поставьте в cоответствие каждому интервалу характеристику функции или её производной. 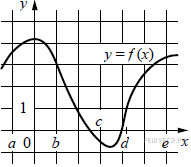
Ниже указаны значения производной в данных точках. Пользуясь графиком, поставьте в соответствие каждой точке значение производной в ней. | ТОЧКИ | | ЗНАЧЕНИЯ ПРОИЗВОДНОЙ | | А) (a; b) Б) (b; c) В) (c; d) Г) (d; e) | | 1) производная отрицательна на всём интервале 2) производная положительна в начале интервала и отрицательна в конце интервала 3) функция отрицательна в начале интервала и положительна в конце интервала 4) производная положительна на всём интервале | Запишите в ответ цифры, расположив их в порядке, соответствующем буквам: |
|
|
| | задача | решение | Теоретические знания | Замечания к решению | |
Прямая y = 3x + 1 является касательной к графику функции ax2 + 2x + 3. Найдите a
|
|
|
|
Представитель от группы идет в соседнюю группу, участники соседней группы проверяют решение и пишут замечание если есть презентация решенных задач, предложенных группам (представители от группы выходят и защищают свои работы и вывешивают решение на доске)
Задание на дом: карточки физический смысл производной Рефлексия: прием оратора (выбирают представителя от группы который должен за 1 мин убедить своих одноклассников как эта тема им жизненно необходима)
| 






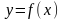 . Прямая, проходящая через начало координат, касается графика этой функции в точке с абсциссой 8. Найдите
. Прямая, проходящая через начало координат, касается графика этой функции в точке с абсциссой 8. Найдите 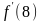 .
. 
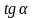
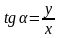
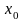 . Найдите значение производной функции
. Найдите значение производной функции 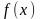 в точке
в точке 
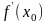 =
=











