Урок- практикум по теме "Использование графов при решении практических задач"

Федосеева Ирина Евгеньевна МАОУ «Гимназия №39» г. Владимир

Конспект урока по вероятности и статистике в 7 классе по теме

по теме «Использование графов при решении задач»

Цели урока:

Научить детей новым способам нахождения знания, ввести новые правила; узнав новые термины и правила, реализовать эти знания на уроке, применив их на практике.

Задачи урока: 

• образовательные: познакомиться с теорией графов; с решением задач с использованием графов;

• развивающие: развитие коммуникативности, навыков само- и взаимоконтроля, математического и общего кругозора, мышления, речи, внимания, памяти, умения анализировать, сравнивать, обобщать;

• воспитательные: формирование положительной мотивации и интереса к математике, потребности в приобретении новых знаний; воспитание активности, умения общаться, сотрудничать и работать в группах, воспитание общей культуры.

Формы работы учащихся: фронтальная, индивидуальная, групповая.

Необходимое оборудование:  раздаточный материал, проектор, интернет для выхода на сайт Joyteka.

Ход урока:

1. Организационный момент

Мы продолжаем работать с графами

Древняя китайская мудрость гласит «Я слышу –я забываю, я вижу – я запоминаю, я делаю – я понимаю». Поэтому наша цель сегодня на уроке не только познакомиться с новыми правилами, но реализовать все имеющиеся знания при решении практических задач. 

Итак, запишем тему урока «Использование графов при решении задач»

Давайте вспомним, что мы уже знаем про графы.

Что такое граф?

Что из себя представляют элементы графа? Что они показывают?

Что называется степенью вершины?

Каким свойством обладают степени всех вершины графа?

1. Мотивационный этап

Ребята, а вы любите головоломки.

С давних пор известны и пользуются популярностью головоломки, которые можно объединить под общим названием «одним росчерком». В таких задачах предлагается начертить какую-либо фигуру, не отрывая карандаша от бумаги, и не проводя дважды по одной линии.

Я предлагаю вам порешать головоломки

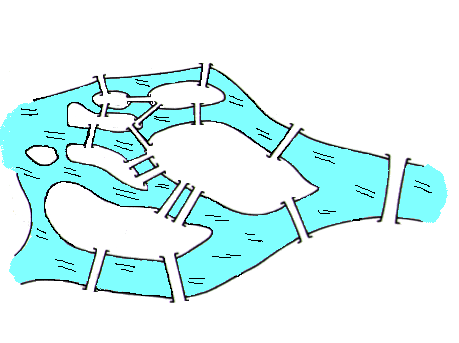
Перед вами фигуры, попробуйте обвести их, не отрывая руки, не проводя по одной линии дважды.(Каждая пара работает самостоятельно.)

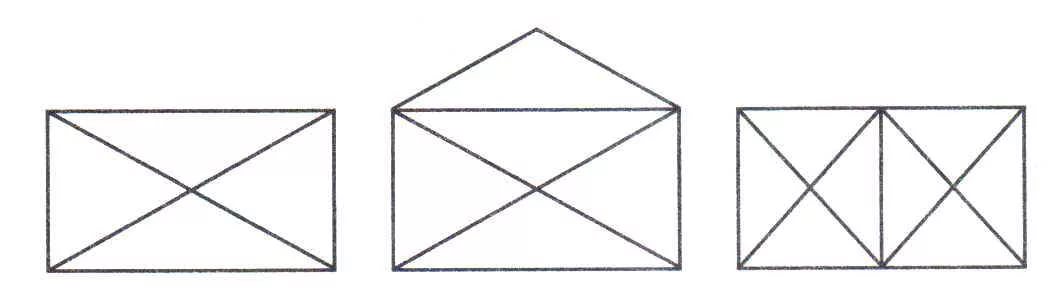
А) Б) В)

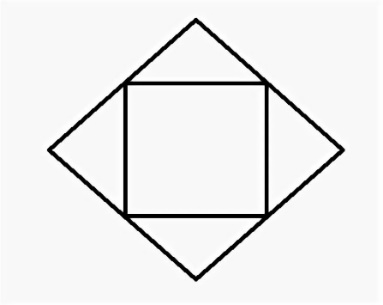
Г) Д)

Предлагаю обсудить задание. У всех ли получилось обвести фигуры? Какие фигуры не удалось обвести? (Обсуждение – каждая группа предлагает, как обвести фигуры, показывает.)

Т.е. мы можем сделать вывод, что не всегда такое задание разрешимо. А как это узнать, чтобы не терять времени, например, на олимпиадах.

Чтобы ответить на этот вопрос познакомимся с одним историческим фактом…

1. Этап осуществления первого пробного действия

Город Кенигсберг стоит на реке Преголь. Некогда там было 7 мостов, которые связывали между собой берега и два острова. У жителей этого города существовало преданье – «Кто совершит прогулку по всем семи мостам, проходя по одному мосту ровно один раз и вернется в исходное место, тот обретет счастье». Многие жители пытались решить эту ГОЛОВОЛОМКУ как теоретически, так и практически, во время прогулок. Впрочем, доказать или опровергнуть возможность существования такого маршрута никто не мог.

В 1736 году задача о семи мостах заинтересовала выдающегося математика, члена Петербургской академии наук. Эйлер выяснил, что такого пути нет и смог это доказать. Конечно, Эйлер решил не только задачу о кенигсбергских мостах, а целый класс аналогичных задач, для которых разработал метод решения. Можно заметить, что задача состоит в том, чтобы по карте провести маршрут – линию, не отрывая карандаша от бумаги, обойти все семь мостов и вернуться в начальную точку. Но Эйлер стал рассматривать вместо карты схему из точек и линий, отбросив мосты, острова и берега, как не математические понятия. Как вы понимаете он задачу решил с помощью графа.

О своем решении Леонард Эйлер написал в письме итальянскому математику и инженеру Мариони, где говорит о том, что Оказывается, все дело в числе ребер, сходящихся в вершине, и там же, в этом письме формулирует правило, по которому быстро определяется можно ли совершить прогулку по всем семи мостам и вернуться обратно . Давайте посчитаем, сколько ребер сходится в каждой вершине (т.е. определим степень каждой вершины) - считаем

Какое же правило сформулировал Эйлер:

Обход возможен:

• Если степень всех вершин четная и его можно начать с любого участка (вернемся в исходную точку)

• Если у 2 вершин степень нечетная, но его нужно начать с одной из нечетных вершин (вернуться в исходное место нельзя, так как обход завершится во второй нечетной вершине)

Обход невозможен, если вершин с нечетной степенью больше 2

Граф, который можно нарисовать, не отрывая карандаша от бумаги, называется эйлеровым

Давайте вспомним с чего мы начали наш урок( с головоломок). Две мы не смогли начертить одним росчерком. Давайте проверим, мы просто не смогли найти решение или эта задача была не разрешима?

1. Этап первичного закрепления нового знания.

Решим похожую задчу о Кенигсбергских мостах

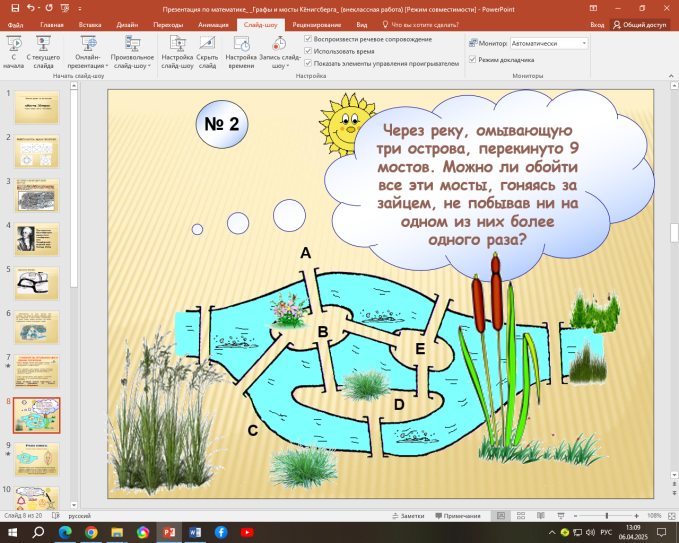
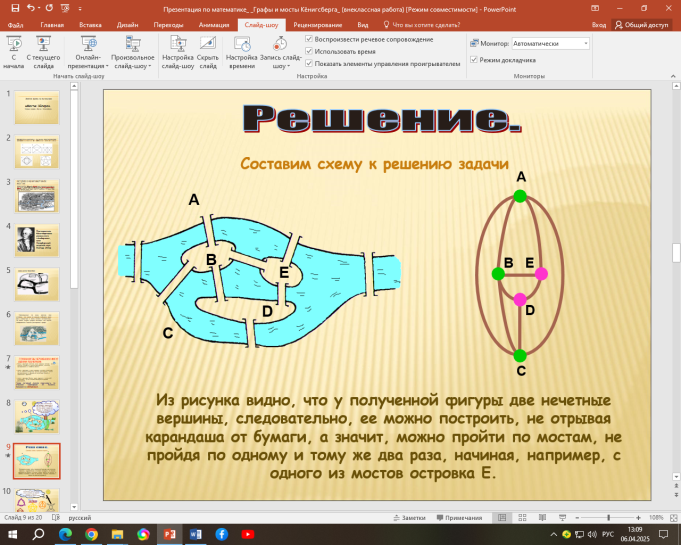
Понятие графа помогает решать не только головоломки, но и комбинаторные (на подсчет различных комбинаций), а также логические задачи.Я предлагаю вам пройти квест. Веб-квест https://joyteka.com/100925860

1. Этап контроля и самопроверки знаний

Предагаю в качестве закрепления материала выполнить синквейн: (слайд)

• 1 строка – одно ключевое слово, определяющее тему урока

• 2строка – два прилагательных, характеризующих ключевое слово

• 3 строка – три глагола, обозначающих действие в рамках заданной темы

• 4 строка – предложение, раскрывающее суть темы

• 5 строка – однослово, описывающее отношение к данной теме урока

Ответ:

1. Граф

2. Эйлеров, ориентированный

3. Описывает отношения, определяет путь, строится

4. С помощью графа можно быстро решить задачу

5. Важная, интересная, полезная и т.д.

1. Домашнее задание

а) Придумать два графа, которые можно обвести одним росчерком и два – которые нельзя. (приготовить карточку с графами для «соседа»).

б)Решить задачу.

Через реку, омывающую шесть островов, переки­нуто семнадцать мостов. Можно ли обойти все эти мосты, не побывав ни на одном из них более одного раза?