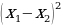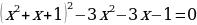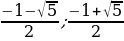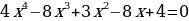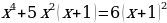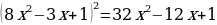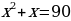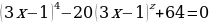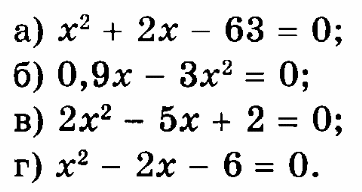Технологическая карта урока
Учитель: Бегматова Анна Александровна, учитель математики высшей квалификационной категории.
Предмет: алгебра
Класс: 8 «А»
Тема урока: «Решение квадратных уравнений»
Урок личностно-ориентированный с применением ИКТ.
Цели урока:
1) обеспечить деятельность учащихся по формированию знаний об основных методах квадратных уравнений
2) создать условия для развития логического мышления при подборе метода решения
3) способствовать развитию познавательных и исследовательских умений учащихся, повышению культуры общения
4) способствовать развитию у учащихся навыков и самоконтроля знаний
Применяемые формы работы: фронтальная, групповая, индивидуальная работа
Оборудование и материалы: УМК «Алгебра 8 класс» А.Г. Мерзляк, В.Б. Полонский, М.С. Якир; пакет раздаточных материалов, листы рефлексии, мульти-медиа-проектор, ноутбуки.
УМК: «Алгебра 8 класс» А.Г. Мерзляк, В.Б. Полонский, М.С. Якир Алгебра учебник
Структура урока
| Этап урока | Задачи этапа | Деятельность учителя | Деятельность учеников | Время (в мин) | Формируемые УУД |
| 1. Организационный этап | Создать благоприятный психологический настрой на работу | Приветствие, проверка подготовленности к учебному занятию, организация внимания детей.
| Включаются в деловой ритм урока.
| 1 | Коммуникативные: планирование учебного сотрудничества с учителем и сверстниками. Регулятивные: организация своей учебной деятельности Личностные: мотивация учения |
| 2. Целеполагание и совместное определение задач урока. Мотивация учебной деятельности учащихся. | Обеспечение мотивации учения детьми, принятие ими целей урока. | Мотивирует учащихся, вместе с ними определяет цель урока; акцентирует внимание учащихся на значимость темы. | Записывают дату в тетрадь, определяют тему и цель урока. | 4 | Познавательные: умение осознанно, самостоятельно формулировать познавательные цели Личностные: самоопределение. Регулятивные: целеполагание. Коммуникативные: умение вступать в диалог, участвовать в коллективном обсуждении вопроса.
|
| 3. Актуализация знаний | Актуализация опорных знаний и способов действий. | Организация устного счета и повторения основных типов задач по теме «Квадратные уравнения». | Участвуют в работе по повторению: в беседе с учителем отвечают на поставленные вопросы. | 10 | Познавательные структурирование собственных знаний. Коммуникативные: организация и планирование учебного сотрудничества с учителем и сверстниками. Регулятивные: фиксация индивидуального затруднения. Личностные: оценивание усваиваемого материала. |
| 4. Применение знаний и умений в новой учебной ситуации | Показать разнообразие задач по теме решение квадратных уравнений. | Организация и контроль за процессом решения задач, оказание консультативной помощи затрудняющимся. | Работают над поставленными задачами. | 10 | Познавательные: формирование интереса к данной теме. Личностные: формирование готовности к самообразованию Коммуникативные: оформление своих мыслей в устной форме; взаимодействие в группе. Регулятивные: планирование своей деятельности для решения поставленной задачи и контроль полученного результата. |
| 5. Физкультминутка | Сменить вид деятельности. | Обеспечивает эмоциональную разгрузку учащихся. | Учащиеся сменили вид деятельности и готовы продолжить работу. | 2 |
|
| 6. Контроль усвоения знаний | Дать качественную оценку каждого участника образовательного процесса. | Выявляет качество и уровень усвоения знаний, а также устанавливает причины выявленных ошибок. | Учащиеся анализируют свою работу | 7 | Личностные: формирование позитивной самооценки Регулятивные: умение самостоятельно адекватно анализировать правильность выполнения действий и вносить необходимые коррективы. |
| 7. Рефлексия (подведение итогов урока) | Дать количественную оценку работы учащихся | Подводит итоги работы класса в целом. | Учащиеся сдают карточки самооценивания. | 3 | Регулятивные: оценивание собственной деятельности на уроке
|
| 8. Информация о домашнем задании | Обеспечение понимания детьми содержания и способов выполнения домашнего задания | Дает комментарий к домашнему заданию | Учащиеся записывают в дневники задание, задают уточняющие вопросы. | 3 | Регулятивные: определение деятельности в домашнем задании. |
ХОД УРОКА
Оргмомент
Эпиграф к уроку: «УМ ЗАКЛЮЧАЕТСЯ НЕ ТОЛЬКО В ЗНАНИЯХ, НО И В УМЕНИИ ПРИЛАГАТЬ ЗНАНИЯ НА ДЕЛЕ»
Какова тема урока?
Каковы цели урока?
На уроке следует каждому вести учет правильных ответов с помощью символов «+», «-», чтобы в конце урока оценить свою работу.
Проверка теоретических знаний учащихся
Что необходимо знать для решения квадратных уравнений?
Ответьте на вопросы:
1. Что называется квадратным уравнением? ( Квадратным уравнением называют уравнение вида ax2+bx+c=0, где х – переменная, a,b,c - параметры, причем а не равно 0)
2. Какие виды квадратных уравнений существуют?
3. Назовите формулу корней квадратного уравнения?
4. Сформулируйте теорему Виета?
Решите в тетради уравнения, которые вы увидите на экране
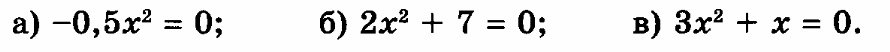
Проверьте себя:
А) х=0
Б) решений нет
В) х=0 или х= - 1/3
Работа в группах. Класс делится на четыре группы
Решение уравнений графическим методом
Решение уравнений по формуле корней квадратных уравнений
Решение уравнений через теорему Виета
Решение уравнений методом замены переменной
Группы получают карточки с заданиями
| Карточка 1 группы «Решение уравнений графическим методом» |
| Решить уравнения: |
А) х2 + 2х – 3 = 0
|
| | Б) х2+ 2 = 1 2 х
|
| Карточка 2 группы «Решение уравнений по формуле корней квадратных уравнений» |
| Решить уравнения: |
А) 3х2 -13х + 4= 0 |
| Б) 25х2 + 60х + 36 = 0 |
| Карточка 3 группы «Решение уравнений через теорему Виета » |
| Решить уравнения: | А) х2 + 2х – 8 =0 |
| Б) х2 – 3х – 18 = 0 |
| Карточка 4 группы « Решение уравнений методом замены переменной» |
| Решить уравнения: | А) х4 - 5х2 -36 = 0 |
| Б) (х2 - 9)2 – 4(х2 – 9) + 3 = 0 |
Обобщение методов решения квадратных уравнений
Представители от каждой группы рассказывают о своём методе решения на примере уравнений из заданий карточки, подготовив решение на доске
Решение заданий 1 группы

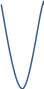

А) х2 + 2х – 3 = 0
Запишем: у = х2
у = -2х +3

х=1 и х = -3
Ответ: -3; 1
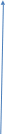

Б) х2+ 2 = 1
2 х

у= х2/2


 у= 1 – 2/х
у= 1 – 2/х
х= - 2
Ответ: -2
Решение заданий 2 группы
А) 3х2 - 13х + 4 = 0
D= 169 – 4 * 3 * 4
D = 121
х= 4
х=1/3
Ответ: 1/3; 4
Решение заданий 3 группы
А) х2 + 2х – 8 =0
х1 + х2 = -2
х1 * х2 = -8
х1=-4
х2 = 2
Ответ: -4; 2
Б) х2 – 3х – 18 = 0
х1 + х2 = 3
х1 * х2 = -18
х1= 6
х2 = -3
Ответ: -3; 6
Решение заданий 4 группы
А) х4 - 5х2 -36 = 0
Пусть х2 = t (t ≥0)
t2 – 5t – 36 = 0
D= 169
t = 9
t = - 4 – не удовлетворяет условию
Обратная замена:
х2 = 9
х = 3 или х = - 3
Ответ: -3; 3
Б) (х2 - 9)2 – 4(х2 – 9) + 3 = 0
Пусть х2 - 9 = t
t2 – 4t + 3 = 0
t1 = 3
t2 = 1
Обратная замена:
х2 - 9 = 3 х2 - 9 = 1
х = 2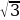 х =
х = 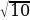
х = - 2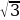 х = -
х = - 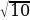
Ответ: - 2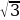 , -
, - 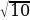 ,
, 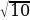 , 2
, 2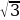
Рефлексия
Выбрать методы решения методов решения предложенных уравнений
Задания выполняются самостоятельно на местах и за доской работают 4 ученика
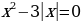
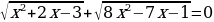
Известно, что х1 и х2 - корни уравнения х2 – 9х + 6 = 0. Не решая уравнение, найдите значение выражения:
А) 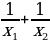 б)
б) 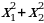 в)
в) 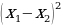
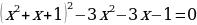
ответы для уравнений:
Ответ: -3; 0; 3
Ответ: 1
Ответ: а) 1,5; б) 69; в) 57
Ответ: -1; 0; 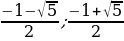
6. Итоги урока. Домашнее задание
Завершая урок, скажите, что нового узнали?
Повторите эпиграф к уроку? (закрыт на дополнительной доске)
Оцените свою работу на уроке самостоятельно по шкале:
| «5» | 14 - 17 балла |
| «4» | 9 - 13 баллов |
| «3» | 5 - 8 баллов |
| «2» | Менее 4 баллов |
Кто оценил свою работу на «5»…
Сдайте тетради.
Возьмите распечатку д/з
Домашнее задание:
каждый ученик получает распечатку с домашним заданием.
а) Для тех кто, получил «5»
1) 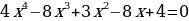
2) 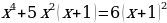
3)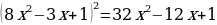
( по желанию)
б) Для тех кто, получил «4»
1) 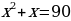
2) -4х = 7х2
3) х2 + 4х + 5 = 0
4) 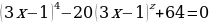
в) Для тех кто, получил «3» или не справился
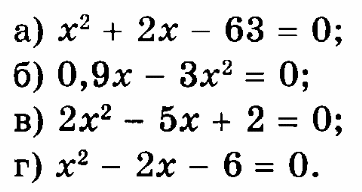












 у= 1 – 2/х
у= 1 – 2/х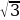 х =
х = 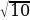
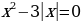
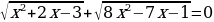
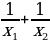 б)
б) 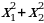 в)
в)