Вариант № 3
1. Задание 1
Укажите наибольшее из следующих чисел:
2. Задание 2
Куриные яйца в зависимости от их массы подразделяют на пять категорий: высшая, отборная, первая, вторая и третья. Используя данные, представленные в таблице, определите, к какой категории относится яйцо, массой 35,5 г.
| Категория | Масса одного яйца, г |
| Высшая | 75,0 и выше |
| Отборная | 65,0 − 74,9 |
| Первая | 55,0 − 64,9 |
| Вторая | 45,0 — 54,9 |
| Третья | 35,0 — 44,9 |
В ответе укажите номер правильного варианта.
1) отборная
2) первая
3) вторая
4) третья
3. Задание 3
На координатной прямой отмечено число a.
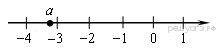
Какое из утверждений относительно этого числа является верным?
В ответе укажите номер правильного варианта.
1) 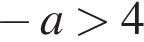
2) 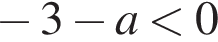
3) 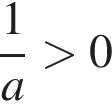
4) 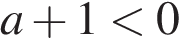
4. Задание 4
Значение какого из выражений является числом рациональным?
В ответе укажите номер правильного варианта.
1) 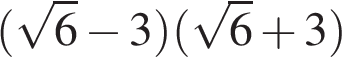
2) 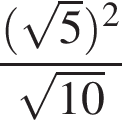
3) 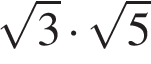
4) 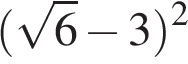
5. Задание 5
На рисунке показано, как изменялась температура воздуха на протяжении одних суток. По горизонтали указано время суток, по вертикали — значение температуры в градусах Цельсия. Найдите наибольшее значение температуры. Ответ дайте в градусах Цельсия.
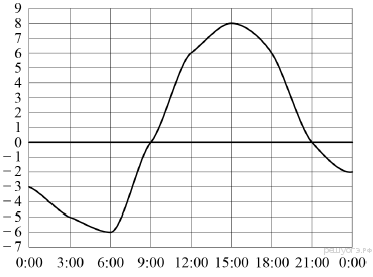
6. Задание 6
Найдите корни уравнения 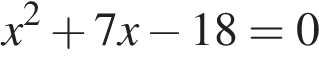 .
.
Если корней несколько, запишите их в ответ без пробелов в порядке возрастания.
7. Задание 7
В городе 70 000 жителей, причем 39% – это пенсионеры. Сколько примерно человек составляет эта категория жителей? Ответ округлите до тысяч.
8. Задание 8
На диаграмме показан возрастной состав населения Японии. Определите по диаграмме, население какого возраста преобладает.
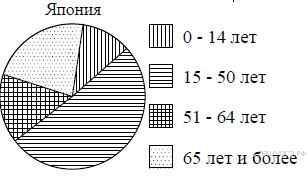
1) 0−14 лет
2) 15−50 лет
3) 51−64 лет
4) 65 лет и более
9. Задание 9
У бабушки 20 чашек: 5 с красными цветами, остальные с синими. Бабушка наливает чай в случайно выбранную чашку. Найдите вероятность того, что это будет чашка с синими цветами.
10. Задание 10
Установите соответствие между функциями и их графиками.
ФУНКЦИИ
А) 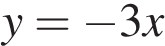
Б) 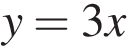
B) 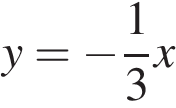
ГРАФИКИ
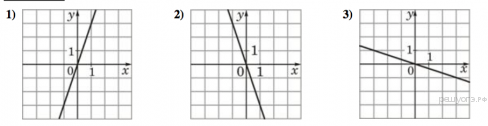 В таблице под каждой буквой укажите соответствующий номер.
В таблице под каждой буквой укажите соответствующий номер.
11. Задание 11
Последовательность задана формулой 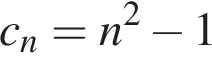 . Какое из указанных чисел является членом этой последовательности?
. Какое из указанных чисел является членом этой последовательности?
12. Задание 12
Найдите значение выражения 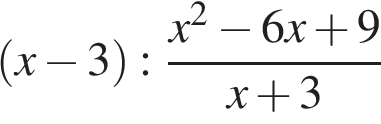 при
при 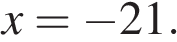
13. Задание 13
В фирме «Чистая вода» стоимость (в рублях) колодца из железобетонных колец рассчитывается по формуле 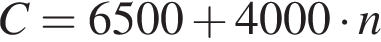 , где
, где 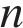 — число колец, установленных при рытье колодца. Пользуясь этой формулой, рассчитайте стоимость колодца из 11 колец.
— число колец, установленных при рытье колодца. Пользуясь этой формулой, рассчитайте стоимость колодца из 11 колец.
14. Задание 14
Решите систему неравенств
На каком рисунке изображено множество её решений?
1) 1
2) 2
3) 3
4) 4
15. Задание 15
Найдите периметр прямоугольного участка земли, площадь которого равна 800 м2 и одна сторона в 2 раза больше другой. Ответ дайте в метрах.
16. Задание 16

ABCDEFGHIJ — правильный десятиугольник. Найдите угол ECI. Ответ дайте в градусах.
17. Задание 17

Найдите ∠KOM, если градусные меры дуг KO и OM равны 112° и 170° соответственно.
18. Задание 18

В трапеции ABCD AD = 5, BC = 2, а её площадь равна 28. Найдите площадь трапеции BCNM, где MN – средняя линия трапеции ABCD.
19. Задание 19
На клетчатой бумаге с размером клетки 1х1 изображён треугольник  . Найдите длину его средней линии, параллельной стороне
. Найдите длину его средней линии, параллельной стороне  .
.
20. Задание 20
Какое из следующих утверждений верно?
1) Любой прямоугольник можно вписать в окружность.
2) Все углы ромба равны.
3) Треугольник со сторонами 1, 2, 4 существует.
21. Задание 21
Решите уравнение
22. Задание 22
По двум параллельным железнодорожным путям в одном направлении следуют пассажирский и товарный поезда, скорости которых равны соответственно 50 км/ч и 40 км/ч. Длина товарного поезда равна 1350 метрам. Найдите длину пассажирского поезда, если время, за которое он прошёл мимо товарного поезда, равно 9 минутам.
23. Задание 23
Постройте график функции Определите, при каких значениях k прямая y = kxимеет с графиком ровно одну общую точку.
24. Задание 24
Окружность с центром на стороне AC треугольника ABC проходит через вершину C и касается прямой AB в точке B. Найдите AC, если диаметр окружности равен 5,25, а AB = 9.
25. Задание 25
 Дан правильный восьмиугольник. Докажите, что если последовательно соединить отрезками середины его сторон, то получится правильный восьмиугольник.
Дан правильный восьмиугольник. Докажите, что если последовательно соединить отрезками середины его сторон, то получится правильный восьмиугольник.
26. Задание 26
Основание AC равнобедренного треугольника ABC равно 12. Окружность радиуса 7,5 с центром вне этого треугольника касается продолжения боковых сторон треугольника и касается основания AC в его середине. Найдите радиус окружности, вписанной в треугольник ABC.
Ключ
| № | Ответ |
| 1 | 3 |
| 2 | 4 |
| 3 | 4 |
| 4 | 1 |
| 5 | 8 |
| 6 | -92 |
| 7 | 27000 |
| 8 | 2 |
| 9 | 0,75 |
| 10 | 213 |
| 11 | 3 |
| 12 | 0,75 |
| 13 | 50500 |
| 14 | 2 |
| 15 | 120 |
| 16 | 72 |
| 17 | 39 |
| 18 | 11 |
| 19 | 3 |
| 20 | 1 |
| 21 | -5; 3; -3 |
Задание 21
Раскладывая на множители левую часть уравнения, получаем Таким образом, корни уравнения
Ответ: −3, 3, −5.
Задание 22
Решение.
Пассажирский поезд движется относительно товарного со скоростью 50 − 40 = 10 км/ч. Проезажая мимо товарного поезда пассажирский проезжает относительного него Следовательно, длина пассажирского поезда составляет 1500 − 1350 = 150 м.
Ответ: 150.
Задание 23
Решение.
Упростим выражение для функции:
(при).
Таким образом, получили, что график нашей функции сводится к графику функции  с выколотой точкой
с выколотой точкой
Построим график функции (см. рисунок).
Заметим, что прямая  проходит через начало координат и будет иметь с графиком функции ровно одну общую точку только тогда, когда будет проходить через выколотую точку Подставим координаты этой точки в уравнение прямой и найдём коэффициент
проходит через начало координат и будет иметь с графиком функции ровно одну общую точку только тогда, когда будет проходить через выколотую точку Подставим координаты этой точки в уравнение прямой и найдём коэффициент 
Ответ: .
Задание 24
Решение.
Пусть О — центр окружности. Радиус окружности, проведённый в точку касания, перпендикулярен касательной. Поэтому треугольник OBA — прямоугольный. Найдём OA по теореме Пифагора:
Следовательно, длина стороны  равна
равна
Ответ: 12.
Задание 25
Решение.
Рассмотрим маленькие треугольники  и , следовательно, эти треугольники равны по двум сторонам и углу. Аналогично равны между собой и остальные маленькие треугольники. Следовательно
и , следовательно, эти треугольники равны по двум сторонам и углу. Аналогично равны между собой и остальные маленькие треугольники. Следовательно
Любой угол правильного восьмиугольника равен Треугольники  и
и  — равнобедренные, углы при основаниях равны Рассмотрим развёрнутый угол
— равнобедренные, углы при основаниях равны Рассмотрим развёрнутый угол 
Аналогично все остальные углы восьмиугольника равны  следовательно восьмиугольник — правильный.
следовательно восьмиугольник — правильный.
Задание 26
Решение.
Введём обозначения, приведённые на рисунке. Лучи  и
и  — соответственно биссектрисы углов
— соответственно биссектрисы углов  и
и  , поскольку эти лучи проходят через центры вписанных окружностей.
, поскольку эти лучи проходят через центры вписанных окружностей.  — середина основания
— середина основания  следовательно Углы и равны друг другу, как углы с взаимно перпендикулярными сторонами. Рассмотрим треугольники и — они прямоугольные и имеют равные углы и , следовательно эти треугольники подобны:
следовательно Углы и равны друг другу, как углы с взаимно перпендикулярными сторонами. Рассмотрим треугольники и — они прямоугольные и имеют равные углы и , следовательно эти треугольники подобны:
Отсюда следует, что радиус вписаной окружности:
Ответ: 4,8.









 В таблице под каждой буквой укажите соответствующий номер.
В таблице под каждой буквой укажите соответствующий номер.









