Вариант 5: Тренировочный вариант ОГЭ по математике 2018г.

Вариант № 5

1. Най­ди­те зна­че­ние вы­ра­же­нию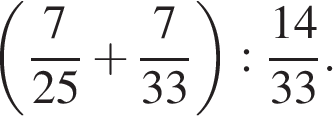  

2.  Дорожный знак, изображённый на рисунке, на­зы­ва­ет­ся «Ограничение высоты». Его уста­нав­ли­ва­ют перед мостами, тон­не­ля­ми и про­чи­ми сооружениями, чтобы за­пре­тить проезд транс­порт­но­го средства, га­ба­ри­ты которого (с гру­зом или без груза) пре­вы­ша­ют установленную высоту.

Какому из дан­ных транспортных средств этот знак за­пре­ща­ет проезд?

В от­ве­те ука­жи­те номер пра­виль­но­го варианта.

1) молоковозу вы­со­той 3770 мм

2) пожарному ав­то­мо­би­лю высотой 3400 мм

3) автотопливозаправщику вы­со­той 2900 мм

4) автоцистерне вы­со­той 3350 мм

3. Известно, что число  отрицательное. На каком из ри­сун­ков точки с ко­ор­ди­на­та­ми  рас­по­ло­же­ны на ко­ор­ди­нат­ной пря­мой в пра­виль­ном порядке?

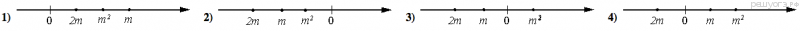
В ответе укажите номер правильного варианта.

4. Расположите в порядке убывания числа: ; ; 6.

В ответе укажите номер правильного варианта.

1) 

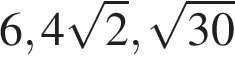
2) 

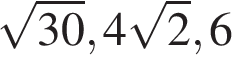
3) 

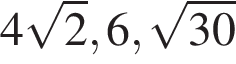
4) 

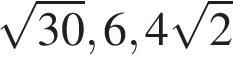
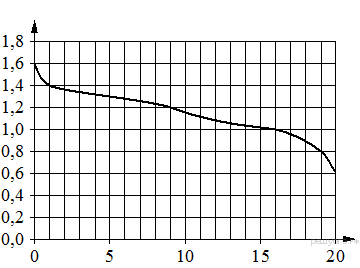
5. При работе фонарика батарейка постепенно разряжается и напряжение в электрической цепи фонарика падает. На графике показана зависимость напряжения в цепи от времени работы фонарика. На горизонтальной оси отмечено время работы фонарика в часах, на вертикальной оси — напряжение в вольтах. Определите по графику, за сколько часов работы фонарика напряжение упадёт с 1,2 В до 0,8 В.

6. Най­ди­те корни урав­не­ния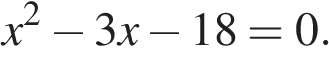 

Если кор­ней несколько, за­пи­ши­те их в ответ без пробелов в порядке возрастания.

7. На пред­при­я­тии ра­бо­та­ло 240 со­труд­ни­ков. После мо­дер­ни­за­ции про­из­вод­ства их число со­кра­ти­лось до 192. На сколь­ко про­цен­тов со­кра­ти­лось число со­труд­ни­ков пред­при­я­тия?

8. На диа­грам­ме по­ка­зан воз­раст­ной со­став на­се­ле­ния России. Опре­де­ли­те по диаграмме, население какого возраста преобладает.

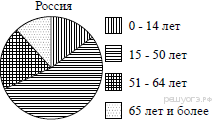
1) 0−14 лет

2) 15−50 лет

3) 51−64 лет

4) 65 лет и более

В ответ запишите номер выбранного варианта ответа.

9. Иг­раль­ную кость бро­са­ют два­жды. Най­ди­те ве­ро­ят­ность того, что оба раза вы­па­ло число, боль­шее 3.

10. На ри­сун­ке изоб­ра­же­ны гра­фи­ки функ­ций вида y = kx + b. Уста­но­ви­те со­от­вет­ствие между зна­ка­ми ко­эф­фи­ци­ен­тов k и b и гра­фи­ка­ми функ­ций.

Графики

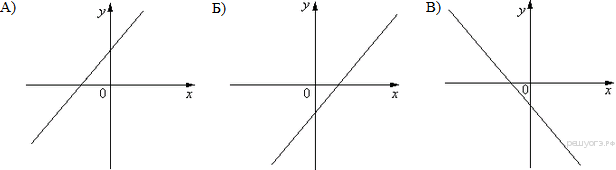
Коэффициенты

Запишите в ответ цифры, рас­по­ло­жив их в порядке, со­от­вет­ству­ю­щем буквам: 

11.Сколько на­ту­раль­ных чисел n удо­вле­тво­ря­ет не­ра­вен­ству ?

12. 

Найдите зна­че­ние вы­ра­же­ния  при x = 6,5, y = −5,2.

13.

Площадь четырёхугольника можно вы­чис­лить по фор­му­ле  где d₁ и d₂ — длины диа­го­на­лей четырёхугольника, α — угол между диагоналями. Поль­зу­ясь этой формулой, най­ди­те длину диа­го­на­ли d₂, если  а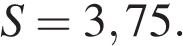 

14.На каком рисунке изображено множество решений неравенства ?

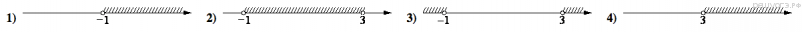
15.

В 60 м одна от дру­гой растут две сосны. Вы­со­та одной 31 м, а дру­гой — 6 м. Най­ди­те расстояние (в метрах) между их верхушками.

16. 

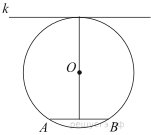
Радиус окруж­но­сти с цен­тром в точке O равен 85, длина хорды ABравна 80 (см. рисунок). Най­ди­те рас­сто­я­ние от хорды AB до па­рал­лель­ной ей ка­са­тель­ной k.

17.Боковая сто­ро­на рав­но­бед­рен­но­го тре­уголь­ни­ка равна 5. Угол при вершине, про­ти­во­ле­жа­щий основанию, равен 120°. Най­ди­те диа­метр окружности, опи­сан­ной около этого треугольника.

18.

Высота BH параллелограмма ABCD делит его сторону AD на отрезки AH = 4 и HD = 65. Диагональ параллелограмма BD равна 97. Найдите площадь параллелограмма.

19. 

На клетчатой бумаге с размером клетки 1×1 изображён ромб. Найдите длину его большей диагонали.

20.Какие из сле­ду­ю­щих утвер­жде­ний верны?

1) Впи­сан­ные углы, опи­ра­ю­щи­е­ся на одну и ту же хорду окружности, равны.

2) Если ра­ди­у­сы двух окруж­но­стей равны 5 и 7, а рас­сто­я­ние между их цен­тра­ми равно 3, то эти окруж­но­сти не имеют общих точек.

3) Если ра­ди­ус окруж­но­сти равен 3, а рас­сто­я­ние от цен­тра окруж­но­сти до пря­мой равно 2, то эти пря­мая и окруж­ность пересекаются.

4) Если впи­сан­ный угол равен 30°, то дуга окружности, на ко­то­рую опи­ра­ет­ся этот угол, равна 60°.

Если утвер­жде­ний несколько, за­пи­ши­те их номера в по­ряд­ке возрастания.

21. 

Решите си­сте­му уравнений  

22. Из пунк­тов А и В, рас­сто­я­ние между ко­то­ры­ми 19 км, вышли од­но­вре­мен­но нав­стре­чу друг другу два пе­ше­хо­да и встре­ти­лись в 9 км от А. Най­ди­те ско­рость пе­ше­хо­да, шед­ше­го из А, если из­вест­но, что он шёл со ско­ро­стью, на 1 км/ч боль­шей, чем пе­ше­ход, шед­ший из В, и сде­лал в пути по­лу­ча­со­вую оста­нов­ку.

23. 

Постройте гра­фик функции  и определите, при каких зна­че­ни­ях m пря­мая y = m не имеет с гра­фи­ком ни одной общей точки.

24. Точка H является основанием высоты BH, проведённой из вершины прямого угла B прямоугольного треугольника ABC. Окружность с диаметром BH пересекает стороны AB и CB в точках P и K соответственно. Найдите PK, если BH = 18.

25. Дана рав­но­бед­рен­ная тра­пе­ция . Точка  лежит на ос­но­ва­нии  и рав­но­уда­ле­на от кон­цов дру­го­го основания. Докажите, что  — середина ос­но­ва­ния .

26. Из вер­ши­ны пря­мо­го угла C тре­уголь­ни­ка ABC про­ве­де­на вы­со­та CP. Ра­ди­ус окруж­но­сти, впи­сан­ной в тре­уголь­ник ACP, равен 12 см, тан­генс угла ABC равен 2,4 . Най­ди­те ра­ди­ус впи­сан­ной окруж­но­сти тре­уголь­ни­ка ABC.

Решение заданий 22-26

№ 22 Решение.

Пусть ско­рость пе­ше­хо­да, шед­ше­го из А — x км/ч, тогда ско­рость вто­ро­го равна (x − 1) км/ч. Пер­вый пе­ше­ход прошёл свою часть пути за , а вто­рой про­де­лал свой путь за . Эти два вре­ме­ни равны, со­ста­вим уравнение:

Корень −3 не под­хо­дит нам по усло­вию задачи. Ско­рость пе­ше­хо­да, шед­ше­го из А, равна 6 км/ч.

Ответ: 6 км/ч.

№ 23 Решение.

Пре­об­ра­зу­ем выражение:  при условии, что x ≠−1. По­стро­им график. Пря­мая y = m не имеет с гра­фи­ком ни одной общей точки при  и 

Ответ: 

№ 24 Решение.

Угол  — вписанный, он равен 90° и опи­ра­ет­ся на дугу следовательно, дуга  равна 180°, значит, хорда  — диа­метр окруж­но­сти и 

Ответ: 18.

№ 25 Решение.

Треугольник  равнобедренный. По­это­му . В рав­но­бед­рен­ной тра­пе­ции .

Отсюда следует, что . Значит, тре­уголь­ни­ки  и  равны по двум сто­ро­нам и углу между ними. Следовательно, .

№ 26 Решение.

Рас­смот­рим угол 

Следовательно тан­ген­сы углов  и  равны.

Рас­смот­рим тре­уголь­ник  тан­генс угла — это от­но­ше­ние про­ти­во­ле­жа­ще­го ка­те­та к прилежащему, следовательно:

Пусть  —  тогда  равно  и, по тео­ре­ме Пифагора, ги­по­те­ну­за  — 

Площадь тре­уголь­ни­ка можно найти как про­из­ве­де­ние его по­лу­пе­ри­мет­ра на ра­ди­ус впи­сан­ной окружности, для пря­мо­уголь­но­го тре­уголь­ни­ка также можно найти площадь, как по­лу­про­из­ве­де­ние катетов. При­рав­няв эти выражения, со­ста­вим уравнение:

Корень ноль не под­хо­дит нам по усло­вию задачи. Сле­до­ва­тель­но  Найдём  из тре­уголь­ни­ка 

Найдём  по тео­рем Пифагора:

Как и в тре­уголь­ни­ке , в тре­уголь­ни­ке  можно найти пло­щадь двумя способами. Со­ста­вим урав­не­ние и найдём ра­ди­ус окружности, впи­сан­ной в тре­уголь­ник 

Ответ: 13.