Практическое занятие
Сечения, развертки многогранников. Различные виды многогранников.
Их изображения.
-
Теоретический этап.
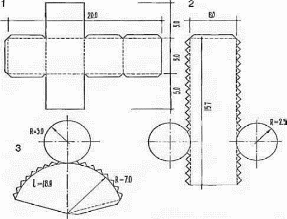
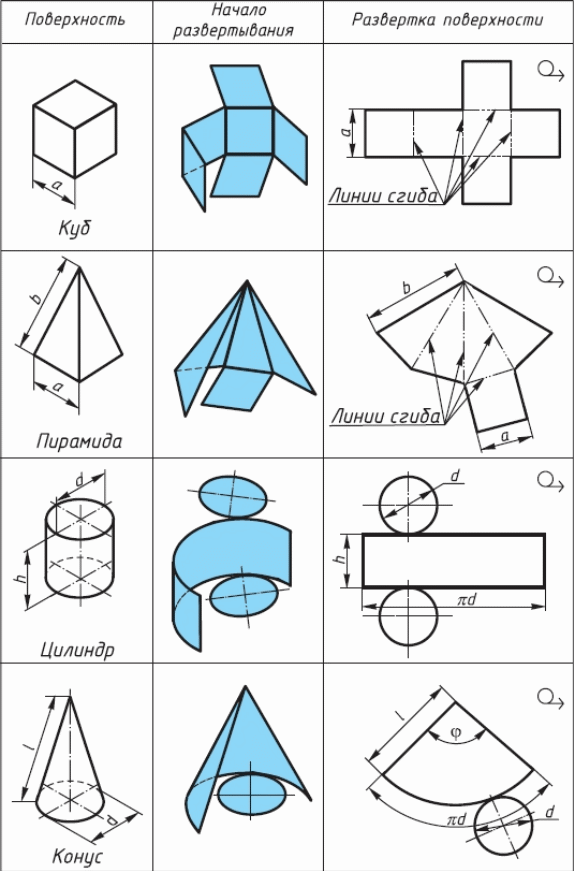
Выкройки макетов простейшей геометрической формы: 1 — куба; 2 — цилиндра; 3 — конуса
Призма
Развертка поверхности прямой призмы представляет собой плоскую фигуру, составленную из боковых граней – прямоугольников и двух равных между собой многоугольников оснований.
Для построения развертки прямой призмы – параллелепипеда, достаточно знать три размера: длину, ширину и высоту призмы (рис. 6).
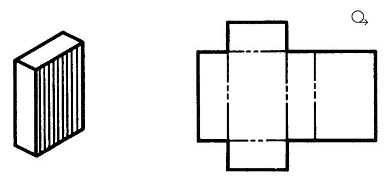
Рис. 6. Развертка поверхности параллелепипеда
Возьмём правильную прямую шестиугольную призму (рис.7). Все боковые грани призмы – прямоугольники, равные между собой по ширине а и высоте Н; основания призмы – правильные шестиугольники со стороной, равной а.
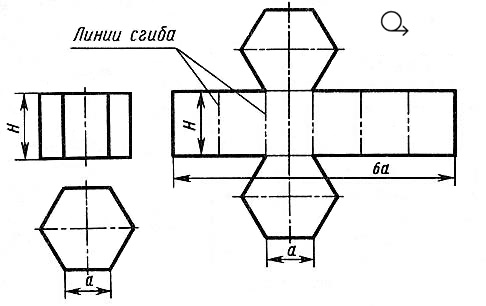
Рис. 7. Развертка поверхности прямой шестиугольной призмы
Так как истинные размеры граней нам известны, нетрудно выполнить построение развертки. Для этого на горизонтальной прямой последовательно откладывают шесть отрезков, равных стороне основания шестиугольника, т. е. 6а. Из полученных точек восставляют перпендикуляры, равные высоте призмы Н, и через конечные точки перпендикуляров проводят вторую горизонтальную прямую. Полученный прямоугольник (Н х 6а) является разверткой боковой поверхности призмы. Затем на одной оси пристраивают фигуры оснований - два шестиугольника со сторонами, равными а. Контур обводят сплошной основной линией, а линии сгиба - штрихпунктирной с двумя точками.
Подобным образом можно построить развертки прямых призм с любой фигурой в основании.
Пирамида
Развертка поверхности правильной пирамиды представляет собой плоскую фигуру, составленную из боковых граней - равнобедренных или равносторонних треугольников и правильного многоугольника основания. Для примера представлены развёртки правильной четырехугольной пирамиды (рис.8) и правильной пятиугольной пирамиды (рис. 9).
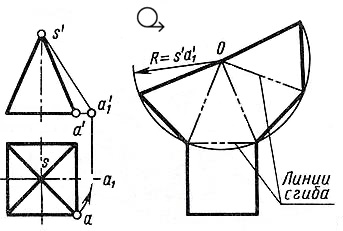
Рис. 8. Развертка поверхности правильной четырёхугольной пирамиды
Решение задачи осложняется тем, что неизвестна величина боковых граней пирамиды, так как ребра граней не параллельны ни одной из плоскостей проекций. Поэтому построение начинают с определения истинной величины наклонного ребра SA. Определив способом вращения (см. рис. 8) истинную длину наклонного ребра SA, равную S'A'1, из произвольной точки О, как из центра, проводят дугу радиусом S'A'1. На дуге откладывают четыре отрезка, равные стороне основания пирамиды, которое спроецировано на чертеже в истинную величину. Найденные точки соединяют прямыми с точкой О. Получив развертку боковой поверхности, к основанию одного из треугольников пристраивают квадрат, равный основанию пирамиды.
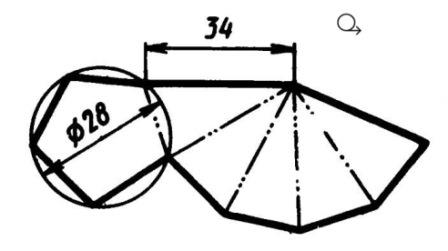
Рис. 9. Развертка поверхности правильной пятиугольной пирамиды
-
Практический этап.
Нужно выполнить развертки различных геометрических тел. У каждого обучающегося к концу урока должна быть – готовая развертка. На столах лежат схемы выполнения разверток и размеры геометрических тел.
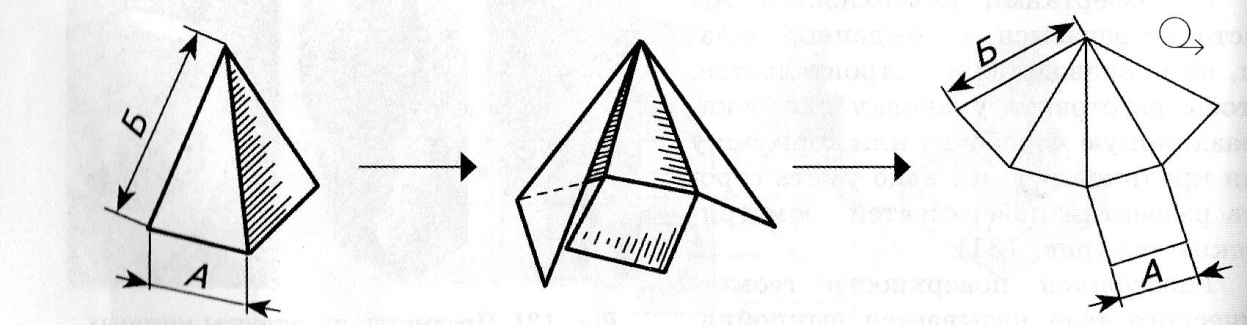
 1. Развертка пирамиды. Б = 50 мм, А = 40 мм.
1. Развертка пирамиды. Б = 50 мм, А = 40 мм.
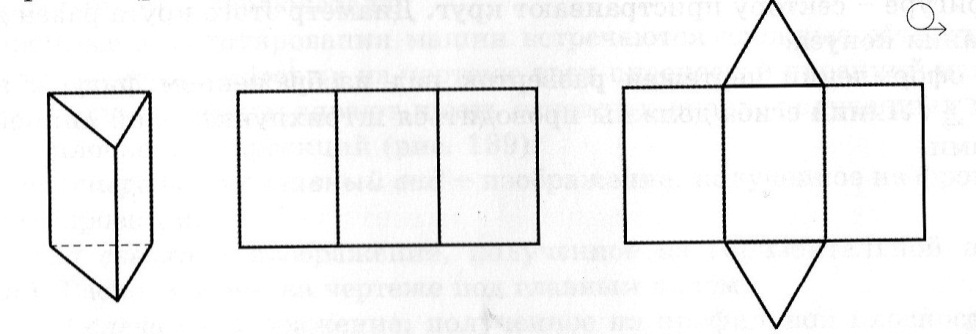
2. Развертка треугольной призмы. Высота призмы h = 40 мм, сторона основания а = 30 мм


3. Развертка куба. Сторона куба а = 30 мм.
4) Дополнительные задания*
Построить развертку многогранника на альбомном листе (или картоне) и склеить.
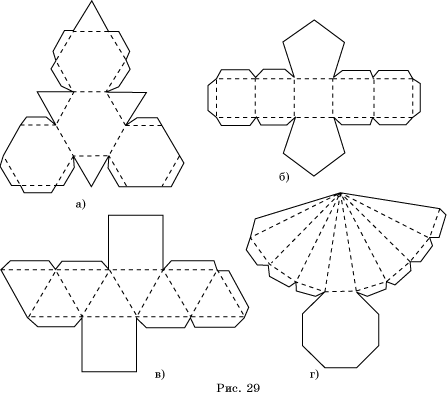











 1. Развертка пирамиды. Б = 50 мм, А = 40 мм.
1. Развертка пирамиды. Б = 50 мм, А = 40 мм.


























