Тема «Возведение в квадрат и куб суммы и разности двух произведений»
Основной задачей является:
- вывести формулы для возведения в квадрат и куб суммы и разности двух выражений; повышение вычислительной культуры учащихся и повышение исторической ценности нашей страны.
Цели:
Образовательная:
- повторить умножение одночлена на многочлен; многочлена на многочлен; разложение многочлена на множители;
- вывести формулы для возведения в квадрат и куб суммы и разности двух выражений; учиться их применять
Развивающая:
- развивать мышление, внимание, память учащихся;
- умение анализировать;
- умение выделять различные этапы решения в нестандартных заданиях.
Воспитательная:
- воспитывать аккуратность, внимательность;
- умение обобщать изученный материал;
- воспитывать патриотизм, повторение истории нашей страны.
Ход урока:
Добрый день! Сегодня необычный урок, урок путешествие назад в прошлое, вспомним или узнаем, что-то новое о истории одного города во время ВОВ. (СЛАЙД 1)
Тему урока мы с вами сформулируем чуть позже. А начнем с эпиграфа:
(СЛАЙД 2) «У математиков существует свой язык и это формулы». Это слова Софьи Васильевны Ковалевской.
У вас на партах есть рабочие листы. В них немного из истории о С.В. Ковалевской. Прочитайте.
Софья Ковалевская стала первой женщиной-математиком в России и первой в мире женщиной-профессором. Однако у нее было еще одно страстное увлечение — она писала книги. В письмах к друзьям она признавалась, что всю жизнь не могла понять, к чему она привязана больше ― к математике или литературе.
Что для вас показалось интересного?
Как вы думаете почему урок был начат со слов
Софьи Ковалевской?
(Будем изучать формулы)
Да, ребята, мы сегодня начинаем с вами изучать новую главу учебника «ФОРОМУЛЫ СОКРАЩЕННОГО УМНОЖЕНИЯ» Сегодня мы познакомимся с некоторыми формулами сокращенного умножения, а вот какими вы мне скажите, когда прочтете тему урока. Возведение в квадрат и куб суммы и разности двух произведений. (СЛАЙД 3) Как понимаете тему?
Тему урока можно записать себе в рабочий лист. А пока пишите, подумайте, какие задачи перед собой ставите. (СЛАЙД 4)
ознакомимся с формулами сокращённого умножения для квадрата и куба суммы и разности двух выражений;
научимся применять эти формулы при упрощении выражений и
решении уравнений.
Как я уже сказала ранее мы сегодня будем с вами путешествовать.
А в какой отправимся город, узнаем в процессе устного счета.
| Б | Е | Л | Г | О | Р | О | Д |
| 8р4-4р5 | -5в8-10в4+30в2 | 3а3-15а2+3а | -12х+24 | -6а3+12а | 8х-14 | 19х+37 | -12х4+8х3-4х2 |
| - 2α (3α2 - 6) | - 5b (b7 +2b3 - 6b) |
| - 6(2х - 4) | 4х(-3х3 + 2х2 - х) |
| 4(2х - 7) | 3α (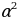 - 5α + 1) - 5α + 1) |
|
| 4р3(2р - р2) |
Ответы:
| 8р4-4р5 (Б) | (О) |
| -12х+24 (Г) | -12х4+8х3-4х2 (Д) |
| 8х-14 (Р) | 3а3-15а2+3а (Л) |
| -5в8-10в4+30в2 (Е) | -6а3+12а (О) |
В рабочих листах у вас есть выражения и есть ответы к ним. Нужно соотнести выражение с правильным ответом. Рядом с ответом буква. Расшифруйте город, в который мы отправимся.
Но перед выполнением вспомним:
Что такое одночлен? Выражения, которые являются произведениями чисел, переменных и их степеней, либо числа, переменные и их степени.
Что такое многочлен? Это сумма одночленов.
Как нам выполнить предложенное задание? (умножим одночлен на многочлен)
ГОРОД БЕЛГОРОД. (СЛАЙД 5)
Что связывает город Белгород и Великую отечественную войну? (1941-1945)
(Там шли сражения) (СЛАЙД 6)
(СЛАЙД Карта сражений) 12 июля 1943 года, под Прохоровкой (в районе деревни Прохоровки Белгородской области) началось крупнейшее танковое сражение в истории человечества. В тот же день Красная армия перешла к наступательным действиям на Курской дуге. Началось напряженное противостояние армий, умов и нервов, которое завершилось победой тех, кто защищал свою Родину. Стратегическая наступательная операция Красной армии получила имя великого русского полководца Михаила Кутузова.
Как называют человека, который защищает свою родину?
ПАТРИОТ (СЛАЙД 7) (СЛАЙД 8-10)
В ваших рабочих листах есть небольшой текст (СЛАЙД 11)
РАБОЧИЙ ЛИСТ
«Битва под Курском — одно из ключевых сражений Великой Отечественной войны, ставшее символом мужества и героизма советских воинов. Прохоровское сражение, произошедшее в ходе битвы, стало одним из самых масштабных танковых боёв в истории».
Какие качества помогли преодолеть врага в этой битве? мужество и героизм
Сейчас мы с вами вместе переведем текст на язык математики, используя формулы сокращённого умножения.
Запишем выражение, которое отражает патриотизм советских солдат в этом сражении. МУЖЕСТВО и ГЕРОИЗМ, где a — мужество, b — героизм
(a+b) Но среди нас есть более мужественные (a + b)2 (a + b)3
(a+b)2 = (a+b)(a+b)= a2+ab+ab+b2=a2+2ab+b2
(a + b)3 = (a+b)(a+b)(a+b)= (a2+2ab+b2)(a+b)=a3+ a2b+2a2b+2ab2 +ab2+ b3= a3+3a2b+3ab2+b3
Формулы учитель выводит на доске. Ученики в рабочих листах
(a + b)2=a2+2ab+b2 квадрат суммы
(a + b)3 a3+3a2b+3ab2+b3 куб суммы
«В ходе Прохоровского сражения советские танкисты проявили невероятную силу духа и стойкость. Они сражались с превосходящими силами противника, демонстрируя мастерство и отвагу».
Представьте, что каждый советский танк — это множитель, а его действия на поле боя — это произведение. Используя формулы сокращённого умножения квадрата разности и куба разности, запишите выражение, которое показывает вклад каждого танка в общую победу. где a — мастерство, b — то что мешает солдату) – нерешительность, ранение, болезнь… у каждого солдата свое мастерство…..
Упростите это выражение и объясните его смысл.
(a - b)2=(a-b)(a-b)=a2-ab-ab+b2=a2-2ab+b2 квадрат разности
(a - b)3=(a-b)(a-b)(a-b)= (a2-2ab+b2)(a-b)=a3-a2b-2a2b+2ab2+ab2-b3= =a3-3a2b+3ab2-b3 куб разности
Формулы учитель выводит на доске. Ученики в рабочих листах
(a - b)2= a2-2ab+b2 квадрат разности
(a - b)3= a3-3a2b+3ab2-b3 куб разности
В учебнике есть определения предложенных формул (стр 166-167). Прочтите это определения.
| (а + в) 2 = а2 + 2ав + в2
квадрат суммы двух выражений | Квадрат суммы двух выражений равен квадрату первого выражения, плюс удвоенное произведение первого выражения на второе и плюс квадрат второго выражения. |
| (а – в) 2 = а2 – 2ав + в2
квадрат разности двух выражений | Квадрат разности двух выражений равен квадрату первого выражения, минус удвоенное произведение первого выражения на второе и плюс квадрат второго выражения. |
| (а + в) 3 = а3 + 3а2в + 3ав2 + в3
куб суммы двух выражений | Куб суммы двух выражений равен кубу первого выражения, плюс утроенное произведение квадрата первого выражения на второе, плюс утроенное произведение первого выражения на квадрат второго, плюс куб второго выражения. |
| (а – в) 3 = а3 – 3а2в + 3ав2 – в3 куб разности двух выражений | Куб разности двух выражений равен кубу первого выражения, минус утроенное произведение квадрата первого выражения на второе, плюс утроенное произведение первого выражения на квадрат второго, минус куб второго выражения. |
Рабочий лист
Заполни пропуски.

Квадрат суммы двух выражений равен _______________ первого выражения ______ удвоенное произведение ___________________________ и плюс квадрат _____________________. (а + в)2 = _________________________.

Квадрат разности двух выражений равен _______________ первого выражения ______ удвоенное произведение ___________________________ и плюс квадрат _____________________. (а - в)2 = _________________________.
Проверяем. (СЛАЙД 12-13)
Квадрат суммы двух выражений равен квадрату первого выражения плюс удвоенное произведение первого выражения на второе и плюс квадрат второго выражения. (а + в)2 = а2 + 2· а · в + в2.
Квадрат разности двух выражений равен квадрату первого выражения минус удвоенное произведение первого выражения на второе и плюс квадрат второго выражения. (а - в)2 = а2 - 2· а · в + в2.
| Исходное выражение | Квадрат первого выражения | Удвоенное произведение первого выражения на второе | Квадрат второго выражения | Квадрат исходного выражения. |
| 2в - 3 | (2в)2 = 4в2 | 2 · 2в · 3 =12в | 32 = 9 | (2в - 3)2 = 4в2 - 12в + 9 |
| 3а - 5 |
|
|
|
|
| 0,2 с + 4 |
|
|
|
|
| 5в - 7 |
|
|
|
|

Куб суммы двух выражений равен _______________ первого выражения ______ утроенное произведение ______________первого выражения и _____________ плюс __________ произведение первого выражения и квадрата ________ плюс куб ________________ _______________.
(а + в)3 = ______________________________.
Куб суммы двух выражений равен кубу первого выражения плюс утроенное произведение квадрата первого выражения и второго плюс утроенное произведение первого выражения и квадрата второго плюс куб второго выражения. (СЛАЙД 14)

Куб разности двух выражений равен _______________ первого выражения ______ утроенное произведение ______________первого выражения и _____________ плюс __________ произведение ____________________ и квадрата второго ___________ куб ________________ _______________.
(а + в)3 = ______________________________.
(а + в)3 = a
3+3a
2b+3ab
2+b
3
Куб разности двух выражений равен кубу первого выражения минус утроенное произведение квадрата первого выражения и второго плюс утроенное произведение первого выражения и квадрата второго минус куб второго выражения (а - в)3 = a3-3a2b+3ab2-b3 (СЛАЙД 15)
| Исходное выражение | Куб первого выражения | Утроенное произведение квадрата первого выражения на второе | Утроенное произведение первого выражения на квадрат второго | Куб второго выражения | Куб исходного выражения. |
| 2с + 5 | (2с)3 = 8с3 | 3 · 4с2 · 5 =60с2 | 3 · 2с · 25 =150с | 53 = 125 | (2с + 5)3 = 8с3+60с2+150с+125 |
| 3а - 5 |
|
|
|
|
|
| 0,3 а + 2 |
|
|
|
|
|
| 4в - 6 |
|
|
|
|
|
Рефлексия: слайд СЛАЙД 17, 18







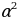 - 5α + 1)
- 5α + 1)












