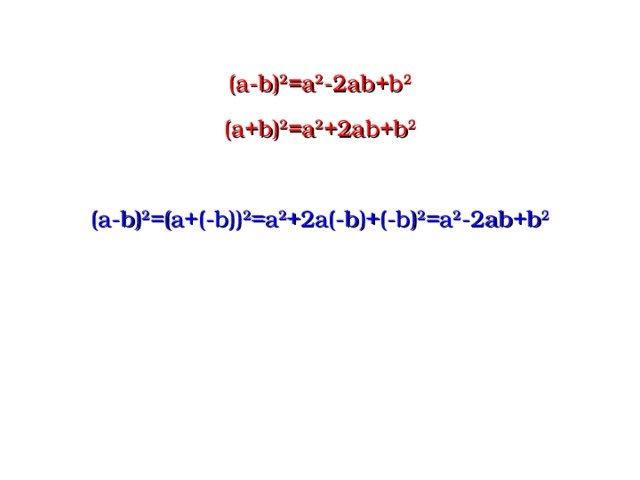Возведение в квадрат суммы и разности

ВОЗВЕДЕНИЕ В КВАДРАТ СУММЫ И РАЗНОСТИ

• ВОЗВЕДЕНИЕ В КВАДРАТ СУММЫ И РАЗНОСТИ
• ВОЗВЕДЕНИЕ В КВАДРАТ СУММЫ И РАЗНОСТИ

(a+b) 2

=

(a+b) 2 =( a+b)(a+b)

=

=a 2 +ab+ab+b 2

=a 2 +2ab+b 2

(a+b) 2 =a 2 +2ab+b 2

ФОРМУЛА КВАДРАТА СУММЫ ДВУХ ВЫРАЖЕНИЙ

КВАДРАТ СУММЫ ДВУХ ВЫРАЖЕНИЙ РАВЕН КВАДРАТУ ПЕРВОГО ВЫРАЖЕНИЯ, ПЛЮС УДВОЕННОЕ ПРОИЗВЕДЕНИЕ ПЕРВОГО И ВТОРОГО ВЫРАЖЕНИЙ, ПЛЮС КВАДРАТ ВТОРОГО ВЫРАЖЕНИЯ.

ПРИМЕР 1:

Представим выражение (5+ 3x ) 2 в виде многочлена.

a 2 +b 2 =a 2 +2ab+b 2

(5+ 3x ) 2 =5 2 +2∙5∙3 x+(3x) 2 = 25+30x+9x 2

ПРИМЕР 2 :

Возведем в квадрат сумму -2a+1

( -2a+1 ) 2

-2a

1

a 2 +b 2 =a 2 +2ab+b 2

( -2a+1 ) 2 = (-2a) 2 +2∙ (-2a) ∙ 1+1 2 = 4a 2 -4a+1

Игорь Жаборовский © 2011

UROKI MATEMATIKI .RU

(a-b) 2

=

(a-b) 2 =( a-b)(a-b)

=

=a 2 -ab-ab+b 2

=a 2 -2ab+b 2

(a-b) 2 =a 2 -2ab+b 2

ФОРМУЛА КВАДРАТА РАЗНОСТИ ДВУХ ВЫРАЖЕНИЙ

КВАДРАТ РАЗНОСТИ ДВУХ ВЫРАЖЕНИЙ РАВЕН КВАДРАТУ ПЕРВОГО ВЫРАЖЕНИЯ, МИНУС УДВОЕННОЕ ПРОИЗВЕДЕНИЕ ПЕРВОГО И ВТОРОГО ВЫРАЖЕНИЙ, ПЛЮС КВАДРАТ ВТОРОГО ВЫРАЖЕНИЯ.

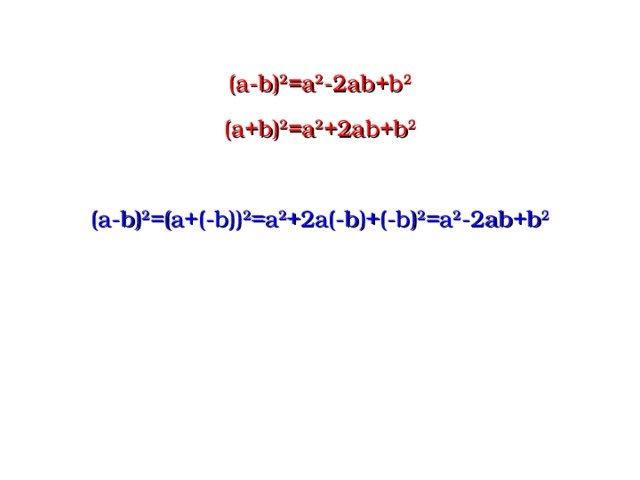
(a-b) 2 =a 2 -2ab+b 2

(a+b) 2 =a 2 +2ab+b 2

(a - b) 2 =(a+( - b)) 2 =a 2 +2a(-b)+(-b) 2 =a 2 -2ab+b 2

ПРИМЕР 3 :

Возведем в квадрат разность 4m-3

(a-b) 2 =a 2 -2ab+b 2

(4m-3) 2

(4m-3) 2 = (4m) 2 - 2∙ 4m ∙ 3+3 2 = 16m 2 -24m+9

ПРИМЕР 4 :

Представим в виде многочлена выражение :

4 x ( x-y ) -(2x-y) 2

4 x ( x-y ) -(2x-y) 2 =

=4x 2 -4xy-(4x 2 -4xy+y 2 )=

=4x 2 -4xy-4x 2 +4xy-y 2 =

=-y 2