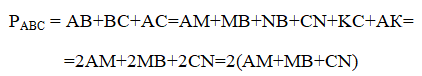Дата:
Тема: ВПИСАННАЯ ОКРУЖНОСТЬ
Задачи: ввести понятие вписанной окружности, закрепить полученные знания в ходе решения задач.
Ход урока
АКТУАЛИЗАЦИЯ ЗНАНИЙ
Сегодня мы начинаем изучать новую тему «Вписанная и описанная окружность». Перед этим проверим, насколько хорошо вы усвоили темы прошлых уроков. Выполните небольшую самостоятельную работу по вариантам.
ИЗУЧЕНИЕ НОВОГО МАТЕРИАЛА
Откройте свои тетради и запишите сегодняшнее число и тему.
Попрошу вас перейти по ссылке и посмотреть объяснение нового материала. Установите время на видео 11:05, в этот момент начинается урок геометрии.
http://1tvcrimea.ru/content/domashnee-zadanie-8-klass-istoriya-geometriya-informatika-vypusk-ot-9042020
Выполните необходимый для вас конспект, приведенный ниже.
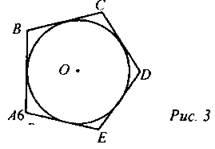
Определение. Если все стороны многоугольника касаются окружности, то окружность называется вписанной в многоугольник, а многоугольник - описанным около этой окружности.
ABCDE — описанный около окружности с центром О пятиугольник. Окружность с центром О вписана в пятиугольник ABCDE. АВ, ВС, CD, DE, АЕ касаются окружности.
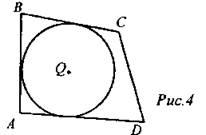
НО. Окружность с центром Q не вписана в четырехугольник ABCD, так как CD не касается окружности.
Теорема. В любой треугольник можно вписать окружность. И при том только одну.
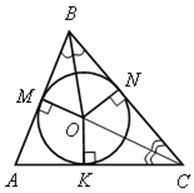
1) Центр вписанной в треугольник окружности в точке пересечения биссектрис;
2) ОМ = ON = ОK= r – радиусы вписанной окружности.
Формула. Площадь треугольника равна произведению его полупериметра на радиус вписанной окружности.
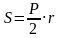 ,
,
где r – радиус вписанной окружности, P – периметр треугольника.
Замечание. В любом описанном четырехугольнике суммы противоположных сторон равны.
И наоборот. Если суммы противоположных сторон выпуклого четырехугольника равны, то в него можно вписать окружность.
ПРАКТИЧЕСКАЯ ЧАСТЬ
Откройте учебники на странице 182 и выполним все вместе № 690. Прочтите внимательно условие задачи. Давайте выполним рисунок и оформим краткую запись к задаче.
№690.
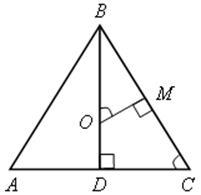
Дано: ABC – равнобедренный треугольник, О – центр вписанной окружности, BD – высота, BO:OD=12:5, АВ=ВС=60 см.
Найти: АС.
Решение.
Т.к. треугольник равнобедренный, то BD – высота, биссектриса, медиана.
Рассмотрим отношение BO:OD=12:5. Пусть k – одна часть этого отношения, тогда BO=12k, OD=5k.
ОМ=ОD как радиусы этой окружности, значит ОМ=5k.
Рассмотрим прямоугольные треугольники ВDС и ВМО. У них общий угол В, и углы BCD=BOM равны между собой (по сумме острых углов), а это значит, 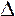 ВDС
ВDС 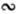
 ВМО по первому признаку. Значит их стороны пропорциональны, получим:
ВМО по первому признаку. Значит их стороны пропорциональны, получим:
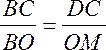
Из прямоугольного треугольника ВDС по теореме Пифагора имеем:
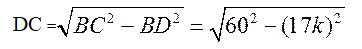
Вернемся к отношению сторон и подставим вместо сторон их значения:
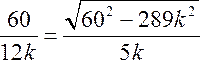
После сокращения и домножения на k, получим:
625 = 3600 – 289k2, откуда выразим 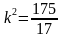
Теперь подставим это значение для нахождения DC:

И так как АС=2 DC, то АС=50 см.
Ответ: 50 см.
№ 693 (а).
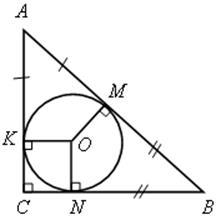
Дано: АВС – прямоугольный треугольник, О – центр вписанной окружности, АВ=26 см, r=4 см.
Найти: Р.
Решение. Докажем, что четырехугольник KONC – квадрат.
АС || ОN, так как АС  СВ и ON
СВ и ON  CВ,
CВ,
СВ || ОK, так как СВ  АС и OK
АС и OK  АС,
АС,
значит, четырехугольник KONC – прямоугольник, а так как KО=CN=r=ON=KC, то KONC – квадрат.
 АKО =
АKО =  АМО (по катету и гипотенузе), поэтому АK = АМ.
АМО (по катету и гипотенузе), поэтому АK = АМ.
 ВNO =
ВNO =  ВМО (по катету и гипотенузе).
ВМО (по катету и гипотенузе).
Распишем периметр треугольника АВС:
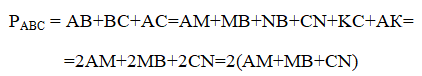
РАВС = 2(АВ + СN) = 2(26 + 4) = 60 (см)
Ответ: 60 см.
ПОДВЕДЕНИЕ ИТОГОВ УРОКА. РЕФЛЕКСИЯ
Ответьте устно на вопросы:
Когда окружность можно вписать в треугольник?
В любой ли четырехугольник можно вписать окружность?
В каком случае в четырехугольник можно вписать окружность?
Домашнее задание: №689, 693(б).










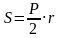 ,
,
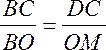
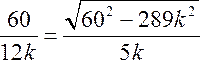
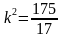


 АKО =
АKО =