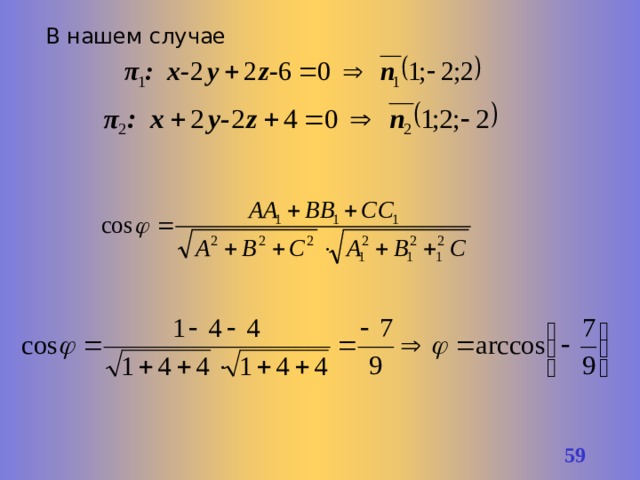Взаимное расположение прямых и плоскостей в пространстве

Взаимное расположение прямых и плоскостей в пространстве

КЭИФ I курс

Преподаватель:

Князева Светлана Евгеньевна

Математика может быть занимательной, математические фокусы — впечатляющими, отношения, в которые вступают между собой цифры — причудливыми. Числа  не управляют миром, но показывают, как  управляется мир.

Иоганн Вольфганг Гёте

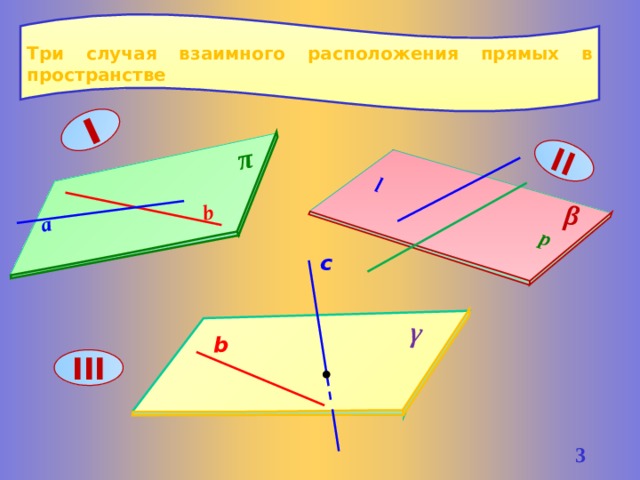
b

l

a

p

π

β

γ

I

II

Три случая взаимного расположения прямых в пространстве

c

b

III

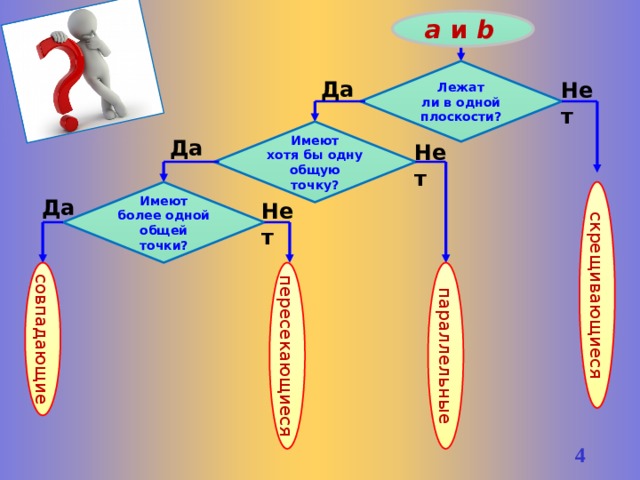
скрещивающиеся

параллельные

пересекающиеся

совпадающие

а и b

Лежат

ли в одной

плоскости?

Да

Нет

Имеют

хотя бы одну

общую

точку?

Да

Нет

Имеют

более одной

общей

точки?

Да

Нет

3

Взаимное расположение прямых в пространстве

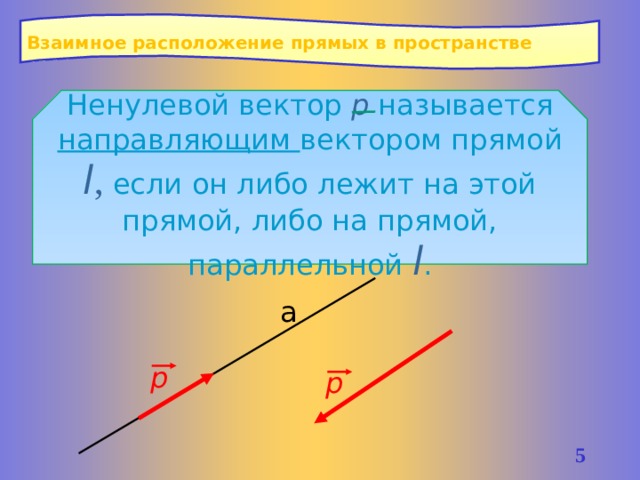
Ненулевой вектор р называется направляющим вектором прямой l , если он либо лежит на этой прямой, либо на прямой, параллельной l .

а

р

р

4

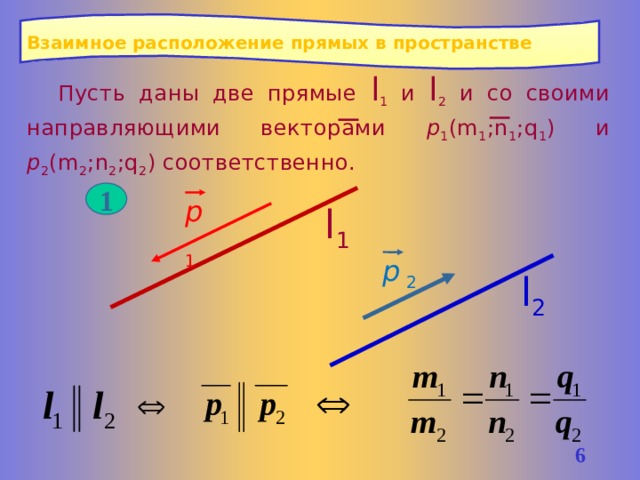
Взаимное расположение прямых в пространстве

Пусть даны две прямые l 1 и l 2 и со своими направляющими векторами р 1 (m 1 ;n 1 ;q 1 ) и р 2 (m 2 ;n 2 ;q 2 ) соответственно.

1

р 1

l 1

р 2

l 2

5

Взаимное расположение прямых в пространстве

Пусть даны две прямые l 1 и l 2 и со своими направляющими векторами р 1 и р 2 соответственно.

2

l 1

l 2

р 1

р 2

6

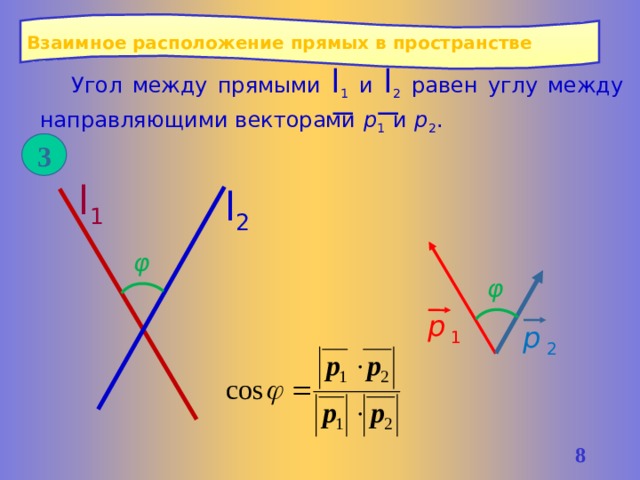
Взаимное расположение прямых в пространстве

Угол между прямыми l 1 и l 2 равен углу между направляющими векторами р 1 и р 2 .

3

l 1

l 2

φ

φ

р 1

р 2

7

n

m

α

β

A

B

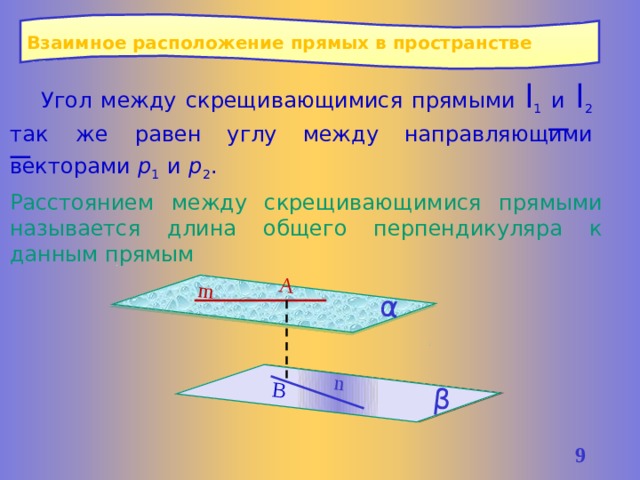
Взаимное расположение прямых в пространстве

Угол между скрещивающимися прямыми l 1 и l 2 так же равен углу между направляющими векторами р 1 и р 2 .

Расстоянием между скрещивающимися прямыми называется длина общего перпендикуляра к данным прямым

8

Геометрия полна приключений, потому что за каждой задачей скрывается приключение мысли. Решить задачу – это значит пережить приключение.

/В. Произволов/

9

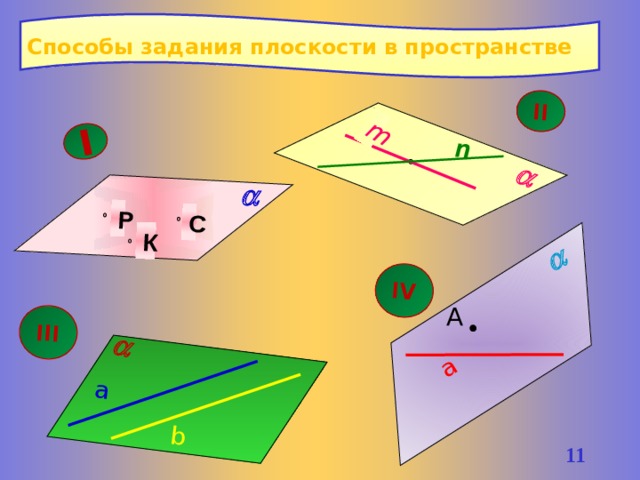
I

II





III



IV

а

b

m

Р

a

n

К



С

Способы задания плоскости в пространстве

A

9



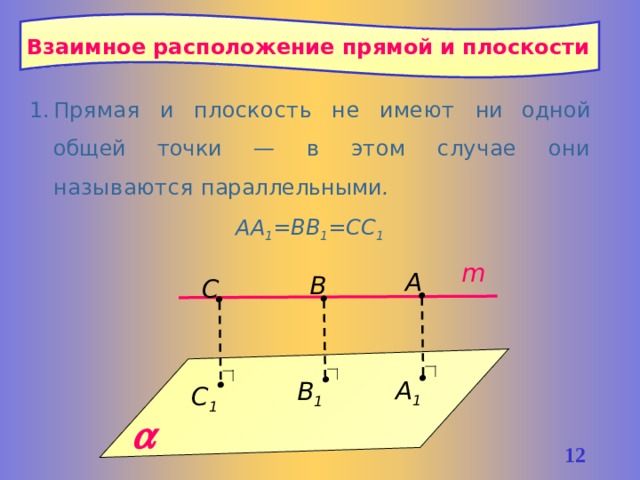
Взаимное расположение прямой и плоскости

• Прямая и плоскость не имеют ни одной общей точки — в этом случае они называются параллельными .

АА 1 =ВВ 1 =СС 1

m

А

В

С

А 1

В 1

С 1

11

а

а

В

В





К

А

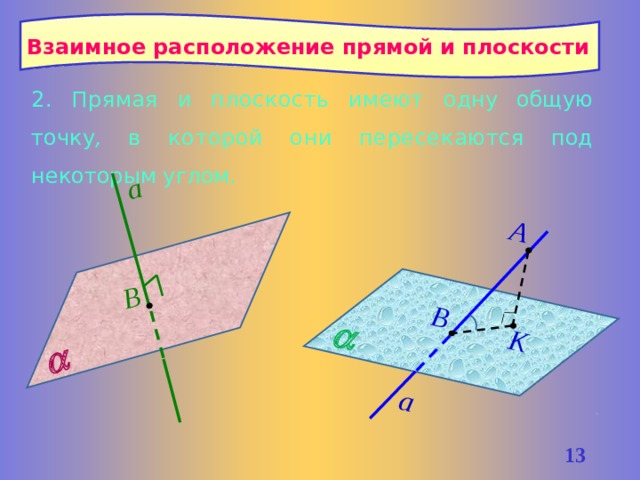
Взаимное расположение прямой и плоскости

2. Прямая и плоскость имеют одну общую точку , в которой они пересекаются под некоторым углом.

12



А

С

В

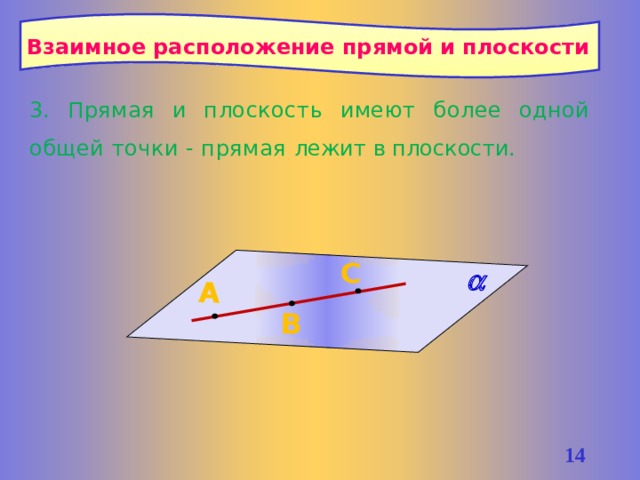
Взаимное расположение прямой и плоскости

3. Прямая и плоскость имеют более одной общей точки - прямая лежит в плоскости.

13

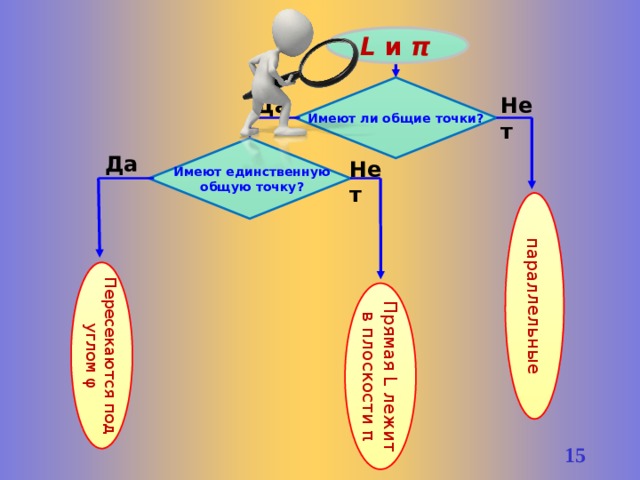
параллельные

Пересекаются под

Прямая L лежит

углом φ

в плоскости π

L и π

Имеют ли общие точки?

Да

Нет

Имеют единственную

общую точку?

Да

Нет

14

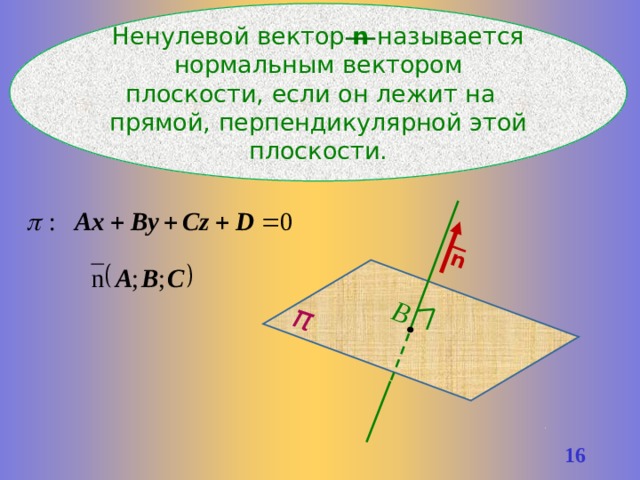
В

π

n

Ненулевой вектор n называется нормальным вектором плоскости, если он лежит на прямой, перпендикулярной этой плоскости.

15

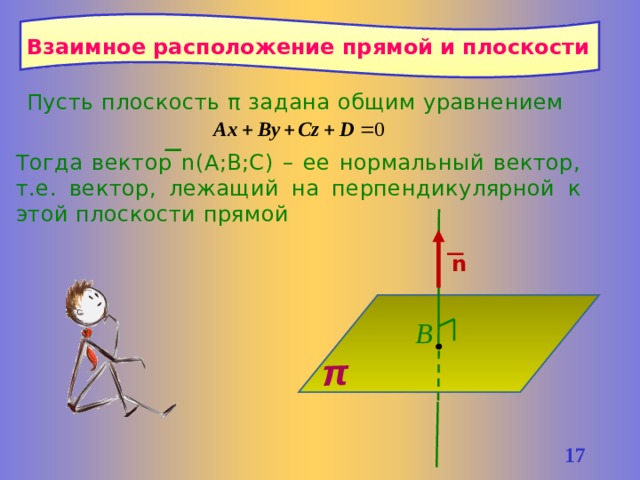
π

Взаимное расположение прямой и плоскости

Пусть плоскость π задана общим уравнением

Тогда вектор n(A;B;C) – ее нормальный вектор, т.е. вектор, лежащий на перпендикулярной к этой плоскости прямой

n

В

16

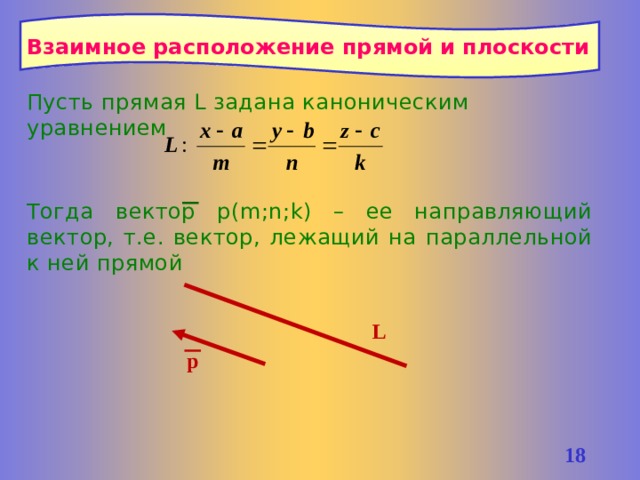
Взаимное расположение прямой и плоскости

Пусть прямая L задана каноническим уравнением

Тогда вектор р(m;n;k) – ее направляющий вектор, т.е. вектор, лежащий на параллельной к ней прямой

L

р

17

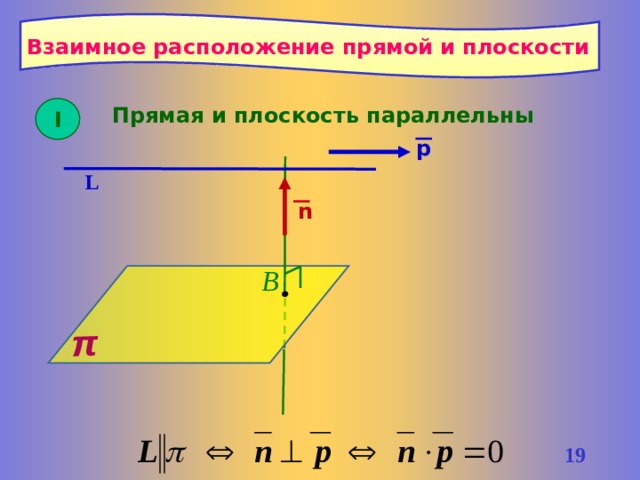
π

Взаимное расположение прямой и плоскости

I

Прямая и плоскость параллельны

p

L

n

В

18

π

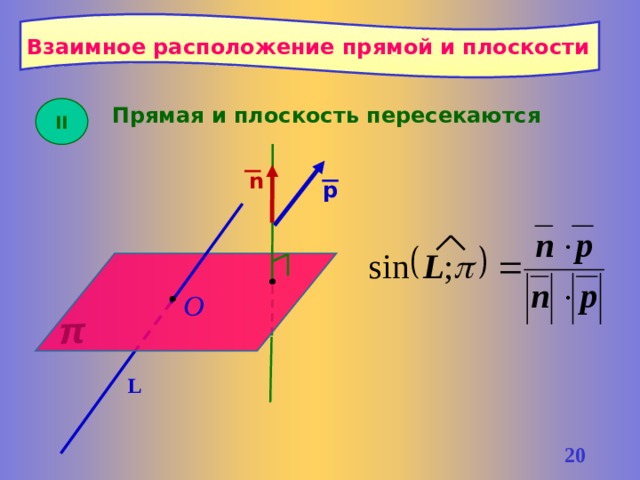
Взаимное расположение прямой и плоскости

Прямая и плоскость пересекаются

II

n

p

О

L

19

О

π

n

p

L

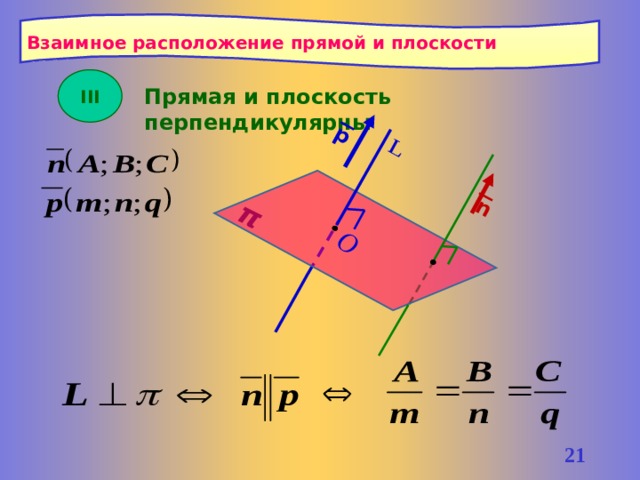
Взаимное расположение прямой и плоскости

III

Прямая и плоскость перпендикулярны

20

Пример 4

Найти точку пересечения прямой L и плоскости π, если

21

Решение

Уравнение прямой L представляет собой тройное равенство. Приравняем каждую часть этого равенства к некоторому параметру t , тогда получим систему:

21

Подставим x , y и z в уравнение плоскости и решим его:

21

Найдем x , y и z , подставляя в последнюю систему уравнений найденное значение t :

Таким образом точка M(11;10;-18) является

точкой пересечения прямой

и плоскости

21

Пример 5

Найти точку пересечения прямой L и плоскости π, если

25

Решение

Уравнение прямой L представляет собой тройное равенство. Приравняем каждую часть этого равенства к некоторому параметру t , тогда получим систему:

25

Подставим x , y и z в уравнение плоскости и решим его:

Прямая и плоскость не имеют общих точек. А, значит, они параллельны.

25

Пример 6

Найти точку пересечения прямой L и плоскости π, если

25

Решение

Уравнение прямой L представляет собой тройное равенство. Приравняем каждую часть этого равенства к некоторому параметру t , тогда получим систему:

25

Подставим x , y и z в уравнение плоскости и решим его:

Прямая и плоскость имеют бесконечно много общих

точек. А, значит, прямая лежит

в плоскости

25

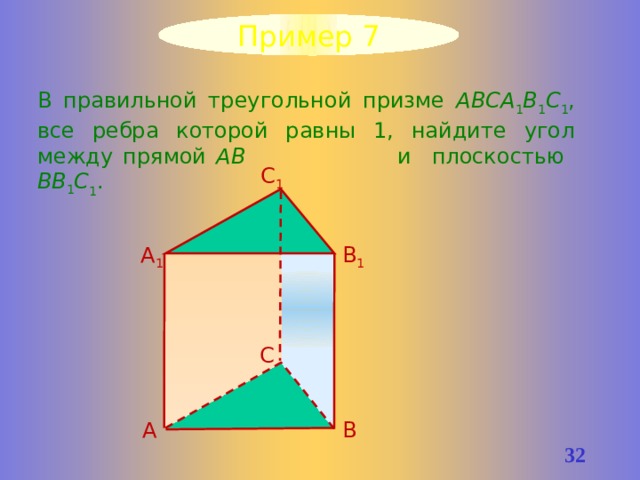
Пример 7

В правильной треугольной призме ABCA 1 B 1 C 1 , все ребра которой равны 1, найдите угол между прямой AB и плоскостью BB 1 C 1 .

С 1

А 1

В 1

С

А

В

31

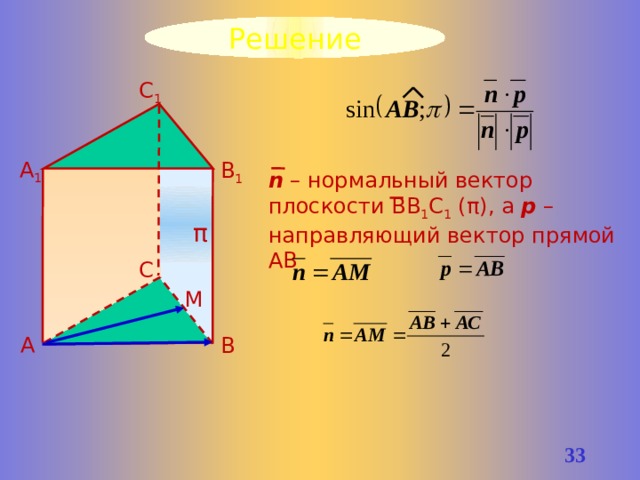
Решение

С 1

А 1

В 1

n – нормальный вектор плоскости ВВ 1 С 1 (π), а р – направляющий вектор прямой АВ

π

С

М

А

В

32

33

33

Пример 8

Дана пирамида с вершиной в точке D(1;10;8), основание которой – треугольник, построенный на векторах АВ и АС. Ребро AD перпендикулярно основанию АВС. Найдите угол между плоскостью основания АВС и боковым ребром СD.

33

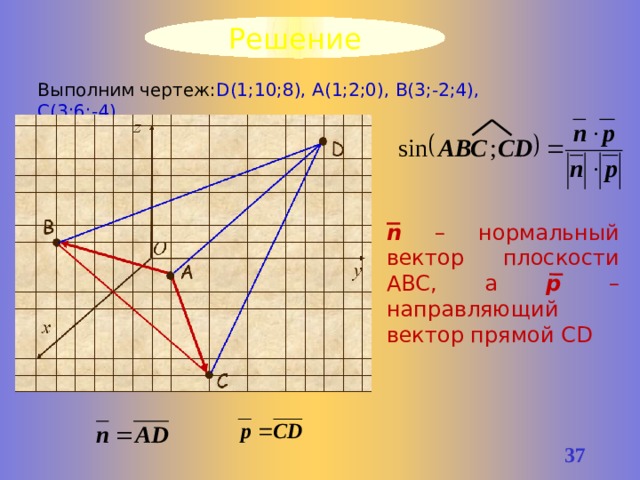
Решение

Выполним чертеж: D(1;10;8), А(1;2;0), B(3;-2;4), C(3;6;-4)

n – нормальный вектор плоскости АВС, а р – направляющий вектор прямой CD

33

D(1;10;8), А(1;2;0), B(3;-2;4), C(3;6;-4)

37

Было бы легче остановить Солнце, легче было сдвинуть Землю, чем уменьшить сумму углов в треугольнике, свести параллели к схождению и раздвинуть перпендикуляры к прямой на расхождение.

/В.Ф. Каган/

37

Взаимное расположение плоскостей

Двугранный угол между плоскостями

Двугранным углом называется фигура, образованная прямой а и двумя полуплоскостями , не принадлежащими одной плоскости, с общей границей а .

Мы знаем, что углы на плоскости (обычные углы) измеряются в градусах. А как измеряются двугранные углы?

37

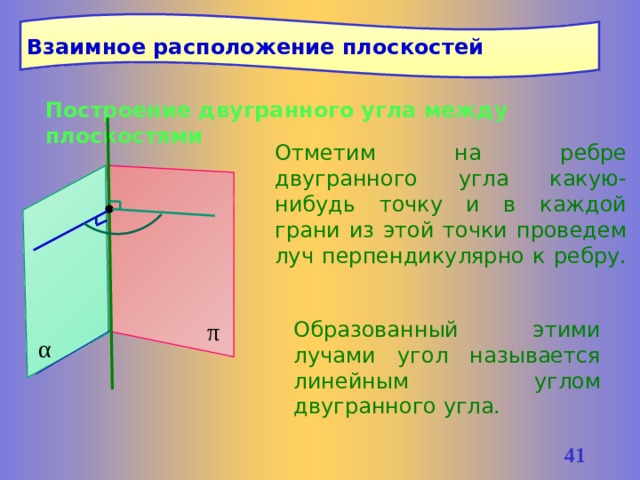
Взаимное расположение плоскостей

Построение двугранного угла между плоскостями

Отметим на ребре двугранного угла какую-нибудь точку и в каждой грани из этой точки проведем луч перпендикулярно к ребру.

Образованный этими лучами угол называется линейным углом двугранного угла.

π

α

37

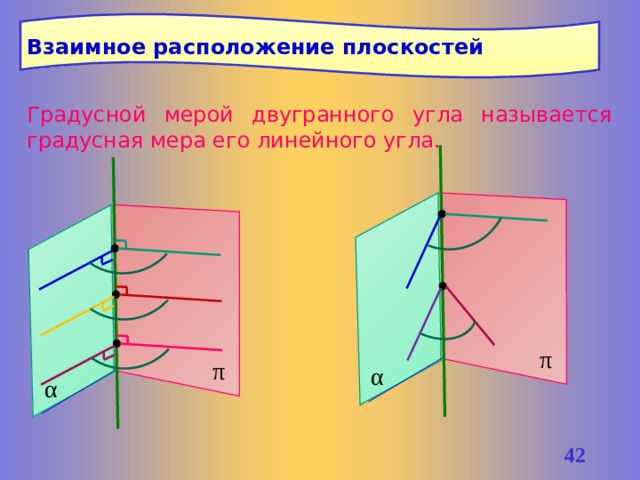
Взаимное расположение плоскостей

Градусной мерой двугранного угла называется градусная мера его линейного угла.

π

π

α

α

41

α

β

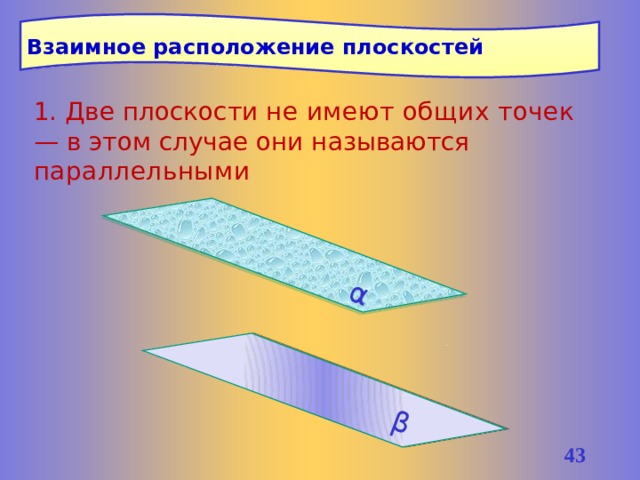
Взаимное расположение плоскостей

1. Две плоскости не имеют общих точек — в этом случае они называются параллельными

42

α

β

с

в

с

в

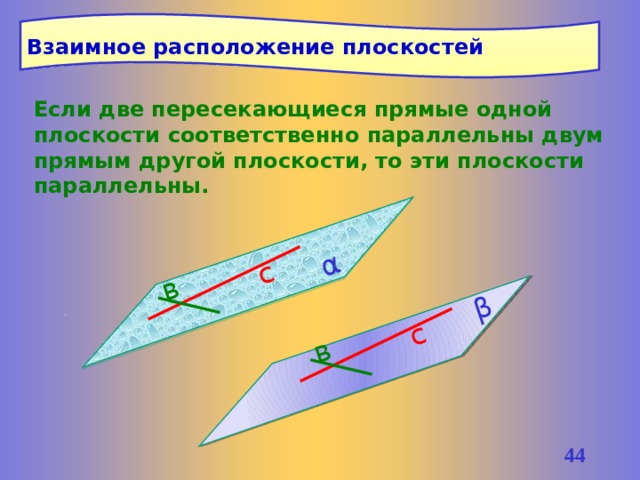
Взаимное расположение плоскостей

Если две пересекающиеся прямые одной плоскости соответственно параллельны двум прямым другой плоскости, то эти плоскости параллельны.

43

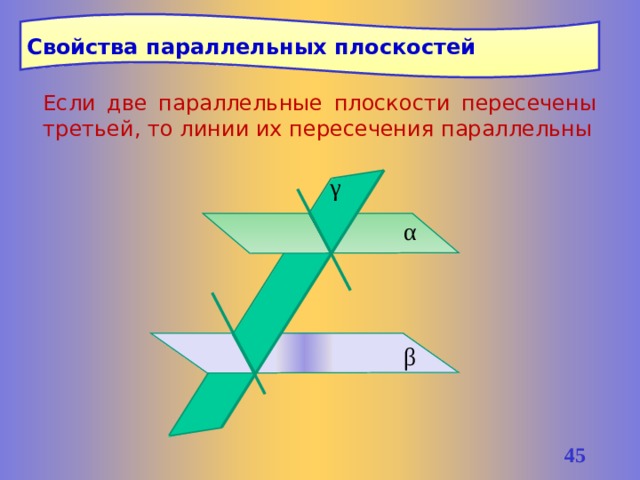
Свойства параллельных плоскостей

Если две параллельные плоскости пересечены третьей, то линии их пересечения параллельны

γ

α

β

44

α

β

А

А 1

В

В 1

С

С 1

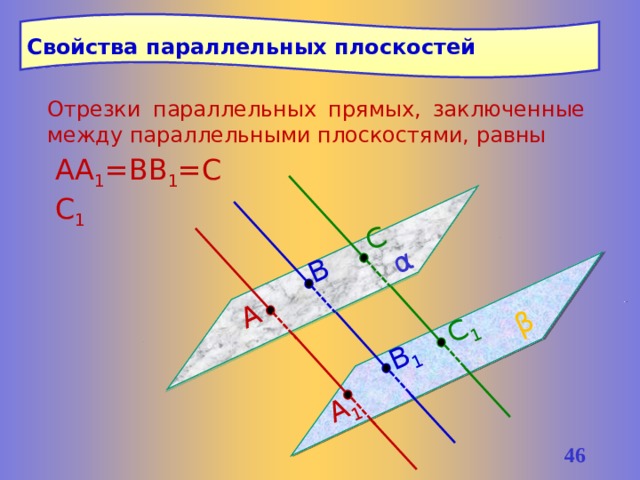
Свойства параллельных плоскостей

Отрезки параллельных прямых, заключенные между параллельными плоскостями, равны

АА 1 =ВВ 1 =СС 1

45

Взаимное расположение плоскостей

2. Две плоскости α и β пересекаются – результатом их пересечения является прямая

α

β

46

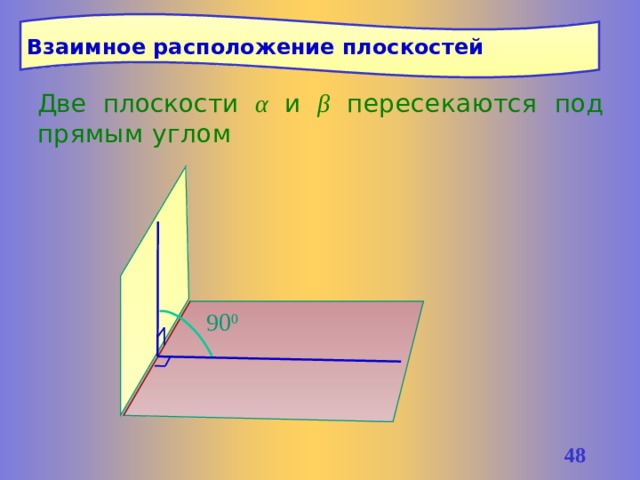
Взаимное расположение плоскостей

Две плоскости α и β пересекаются под прямым углом

90 0

47

90 0

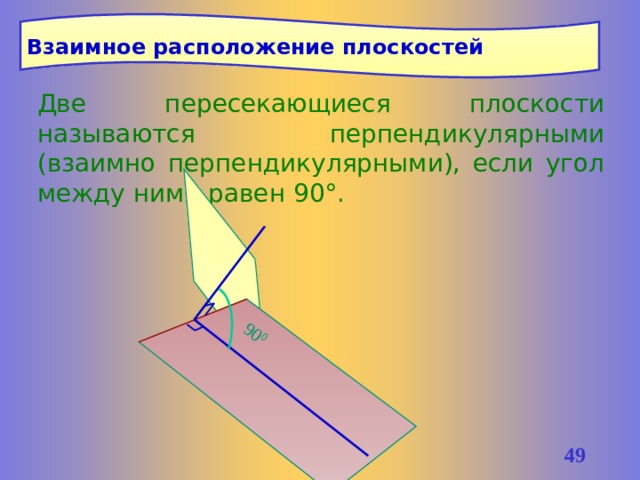
Взаимное расположение плоскостей

Две пересекающиеся плоскости называются перпендикулярными (взаимно перпендикулярными), если угол между ними равен 90°.

48

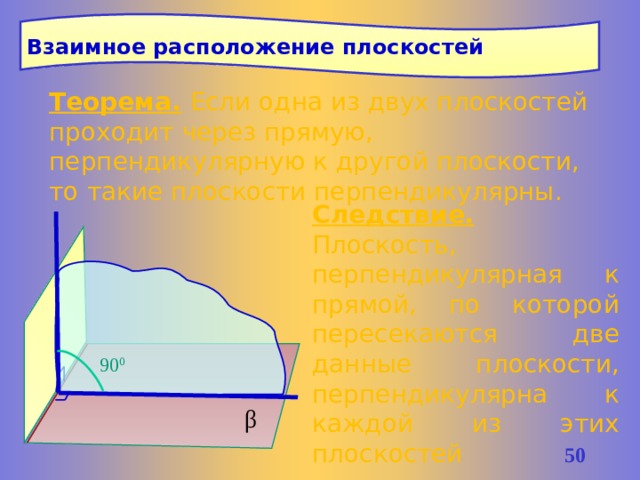
Взаимное расположение плоскостей

Теорема. Если одна из двух плоскостей проходит через прямую, перпендикулярную к другой плоскости, то такие плоскости перпендикулярны.

Следствие. Плоскость, перпендикулярная к прямой, по которой пересекаются две данные плоскости, перпендикулярна к каждой из этих плоскостей

90 0

β

49

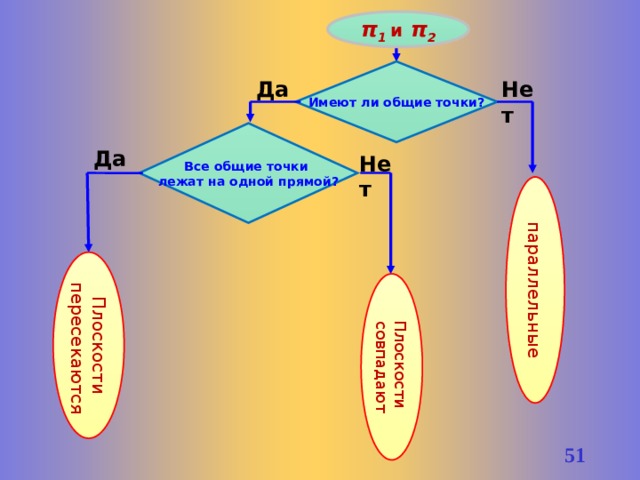
параллельные

Плоскости

Плоскости

совпадают

пересекаются

π 1 и π 2

Имеют ли общие точки?

Да

Нет

Все общие точки

лежат на одной прямой?

Да

Нет

50

π

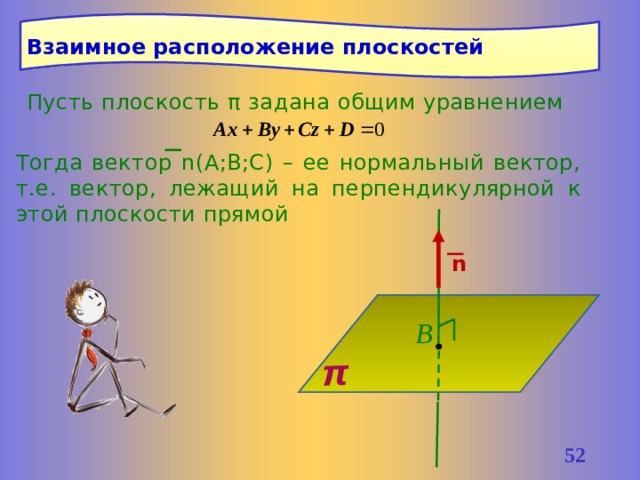
Взаимное расположение плоскостей

Пусть плоскость π задана общим уравнением

Тогда вектор n(A;B;C) – ее нормальный вектор, т.е. вектор, лежащий на перпендикулярной к этой плоскости прямой

n

В

50

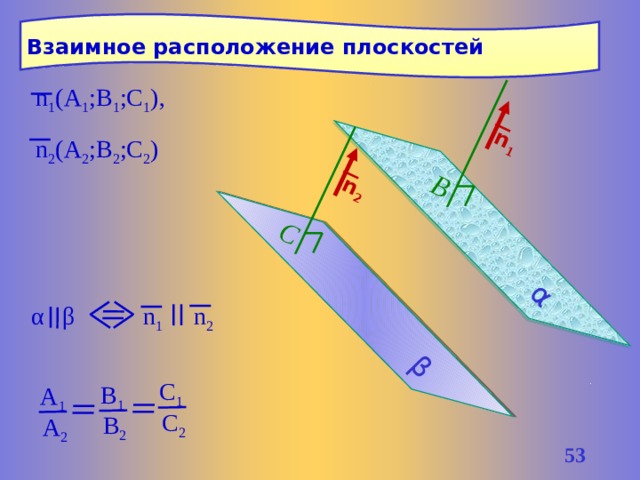
В

α

β

С

n 1

n 2

Взаимное расположение плоскостей

n 1 (A 1 ;B 1 ;C 1 ), n 2 (A 2 ;B 2 ;C 2 )

α β n 1 n 2

C 1

B 1

A 1

C 2

B 2

A 2

52

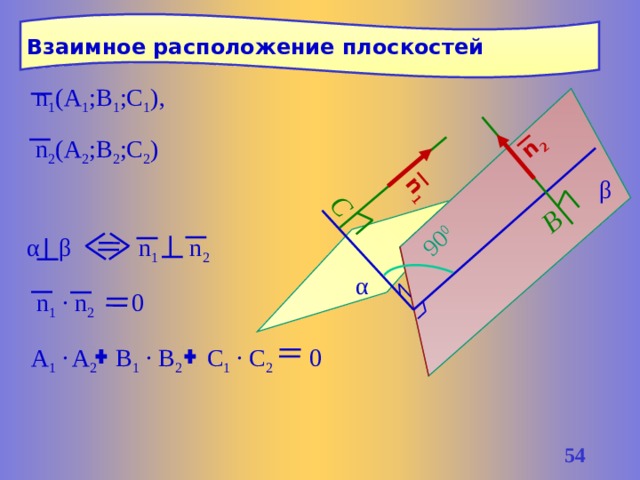
90 0

C

В

n 1

n 2

Взаимное расположение плоскостей

n 1 (A 1 ;B 1 ;C 1 ), n 2 (A 2 ;B 2 ;C 2 )

β

α β n 1 n 2

α

n 1 · n 2 0

A 1 · A 2 B 1 · B 2 C 1 · C 2 0

53

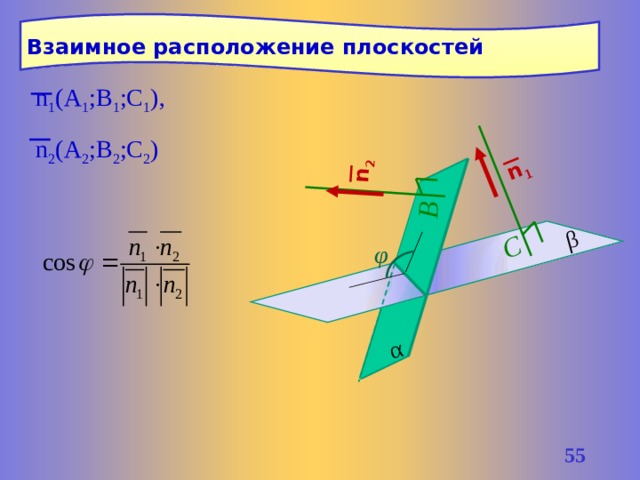
C

В

n 1

n 2

α

β

Взаимное расположение плоскостей

n 1 (A 1 ;B 1 ;C 1 ), n 2 (A 2 ;B 2 ;C 2 )

φ

54

Пример 9

Плоскости π 1, π 2 и π 3 заданы своими общими уравнениями.

• Выяснить взаимное расположение плоскостей π 1 и π 2 .
• При каком значении параметра р

а) плоскость π 3 параллельна плоскости π 1 ;

б) плоскость π 3 перпендикулярна плоскости π 2 ?

55

Решение.

55

55

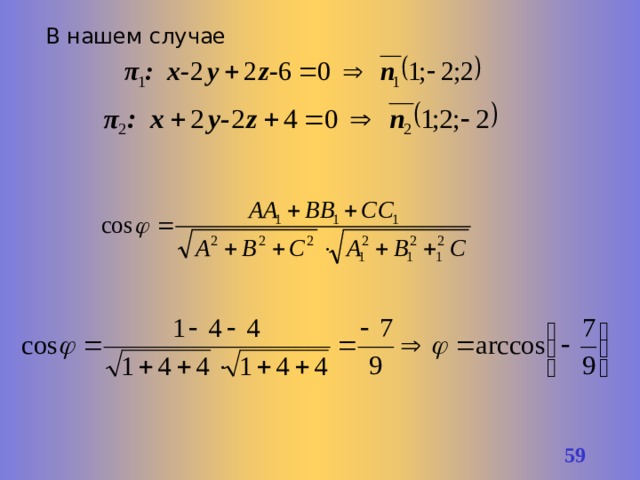
В нашем случае

55

55

55