Взаимное расположение прямых в пространстве

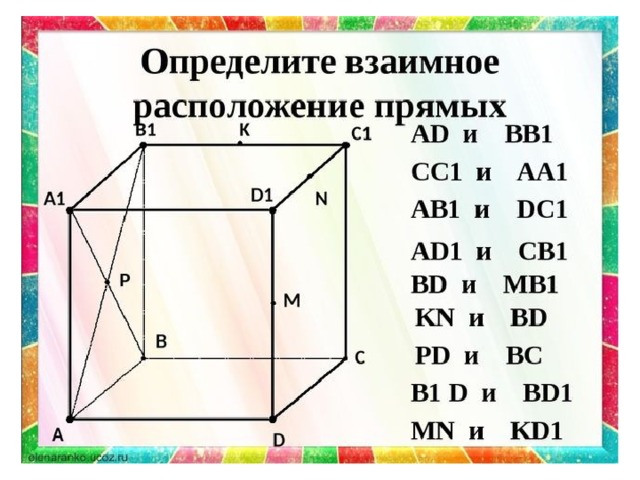
Взаимное расположение двух прямых в пространстве. Параллельность прямой и плоскости. Параллельность плоскостей.

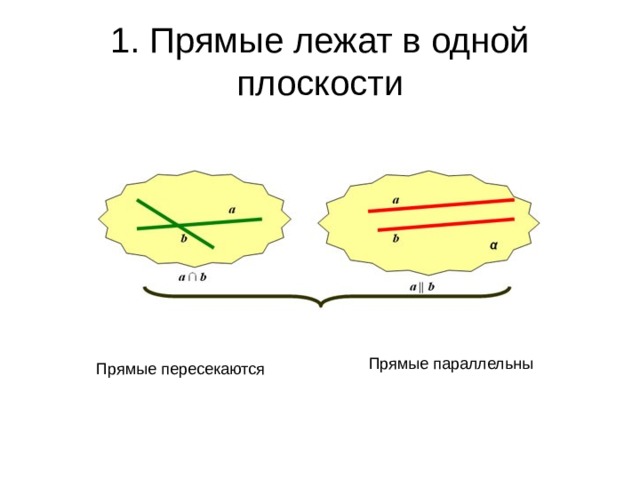
1. Прямые лежат в одной плоскости

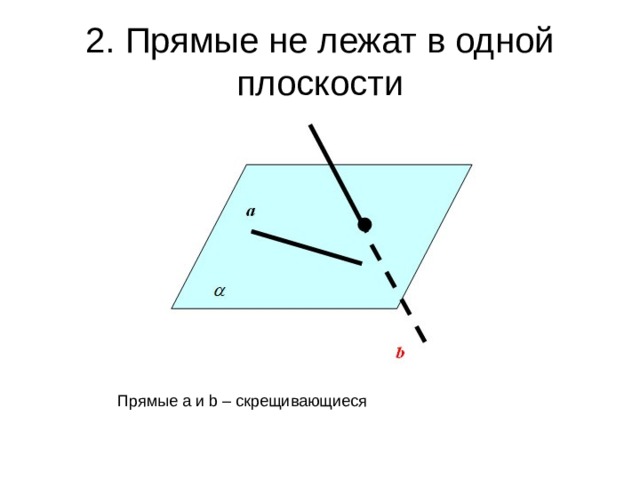
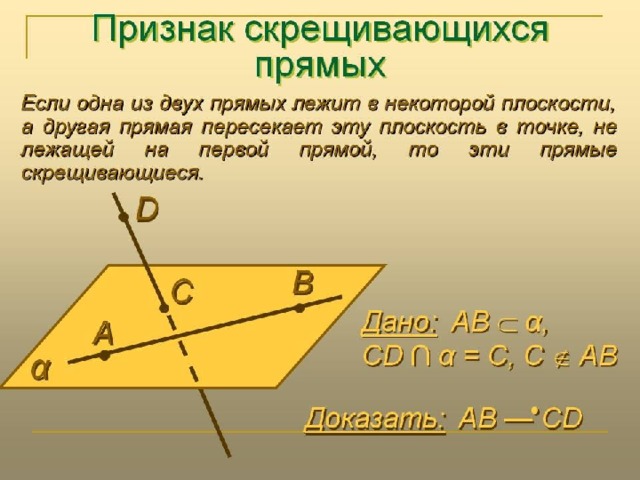
2. Прямые не лежат в одной плоскости

Прямые a и b – скрещивающиеся

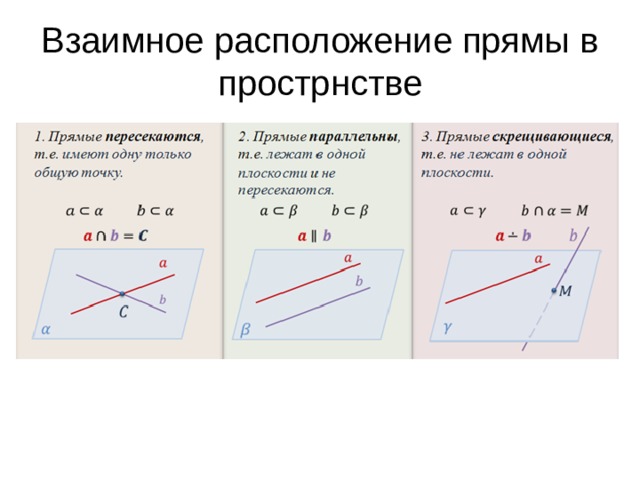
Взаимное расположение прямы в прострнстве

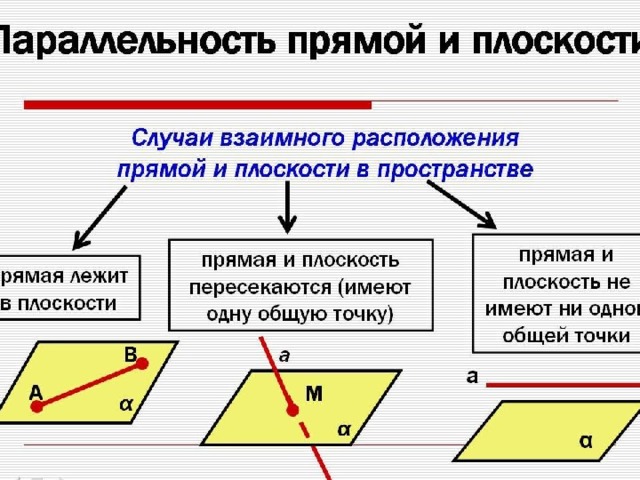
Параллельность прямой и плоскости

Прямая и плоскость называются параллельными , если они не пересекаются.

а 1

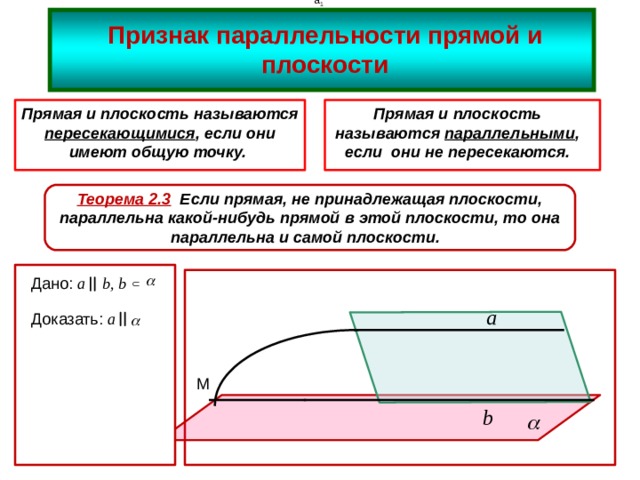
Признак параллельности прямой и плоскости

Прямая и плоскость называются параллельными , если они не пересекаются.

Прямая и плоскость называются пересекающимися , если они имеют общую точку.

Теорема 2.3 Если прямая, не принадлежащая плоскости, параллельна какой-нибудь прямой в этой плоскости, то она параллельна и самой плоскости.

Дано: a b, b

a

Доказать: a

M

b

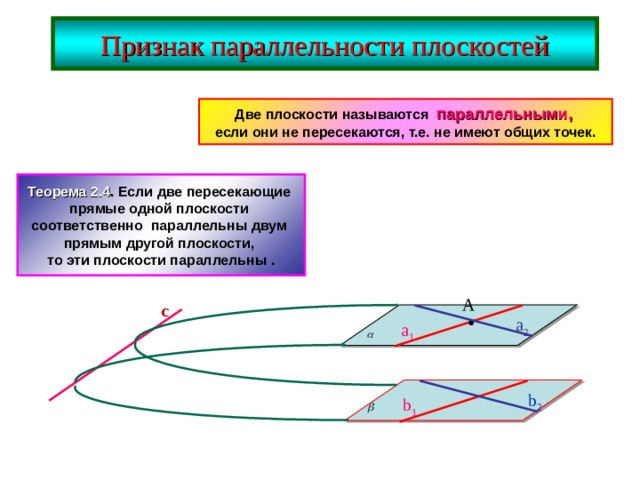
Признак параллельности плоскостей

Две плоскости называются параллельными, если они не пересекаются, т.е. не имеют общих точек.

Теорема 2.4 . Если две пересекающие

прямые одной плоскости

соответственно параллельны двум

прямым другой плоскости,

то эти плоскости параллельны .

A

c

•

a 2

a 1

b 2

b 1

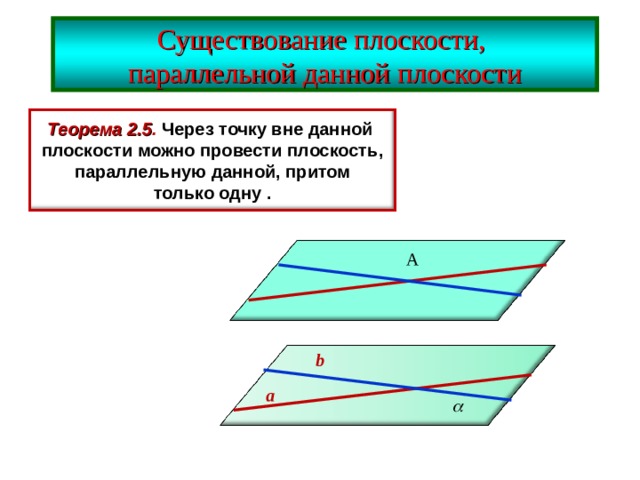
Существование плоскости,

параллельной данной плоскости

Теорема 2.5 . Через точку вне данной

плоскости можно провести плоскость,

параллельную данной, притом

только одну .

A

•

b

a

C войства параллельных плоскостей

Теорема 2. 6 . Если две параллельные

плоскости пересекаются третьей,

то прямые пересечения параллельны

между собой.

a

b

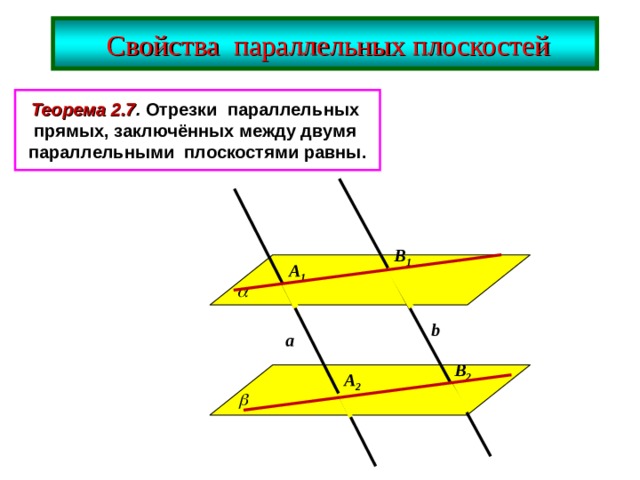
C войства параллельных плоскостей

Теорема 2.7 . Отрезки параллельных

прямых, заключённых между двумя

параллельными плоскостями равны.

B 1

A 1

b

a

B 2

A 2