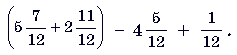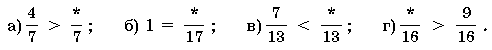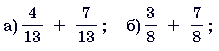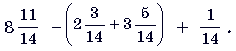Зачеты по математике 5-6 классы

Задания каждой зачетной работы направлены на проверку усвоения основных моментов соответствующей темы курса 5-го или 6-го класса. Работы состоят из двух частей: основной (1–9 задания), где представлены все те типы задач обязательного минимума, которые должны уметь решать школьники, и дополнительной (остальные задания), в которой предлагаются более сложные задания – для учащихся, претендующих на оценку «4» или «5». Таким образом, подготовка и проведение зачетов по таким текстам являются элементом технологии дифференцированного обучения.

При оценивании работ учащихся можно придерживаться следующих ориентиров:

– для получения зачета или любой положительной оценки ученик должен верно решить не менее 6 заданий основной части;
– каждое решенное задание основной части оценивается в один балл, для заданий дополнительной части число баллов указано в работах;
– оценка «3» ставится, если ученик набрал от 7 до 10 баллов; оценка «4» – если набрано от 11 до
15 баллов; оценка «5» – если учеником набрано
не менее 16 баллов.

Зачет N№ 1. Сложение и вычитание натуральных чисел.
Зачет N№ 2. Умножение и деление натуральных чисел.
Зачет N№ 3. Формулы. Измерение площадей и объемов.
Зачет N№ 4. Обыкновенные дроби.
Зачет N№ 5. Сложение и вычитание десятичных дробей.
Зачет N№ 6. Умножение и деление десятичных дробей.
Зачет N№ 7. Проценты.

Зачет №1. Сложение и вычитание натуральных чисел

Вариант № 1

1. Укажите какое из чисел больше: 6912 и 6291.
2. Даны числа: 145, 14, 541, 514, 51 и 544. Расположите эти числа в порядке возрастания.
3. Найдите:

а) разность чисел 68713 и 45687;
б) сумму чисел 23567 и 12386.

4. Вычислите: 365 – (145 – 56) +254.
5. Проверьте, правильно ли выполнены действия:

а) 45731 – 12786 = 32945;
б) 25473 + 45179 = 70662.

6. Решите уравнение 456 – у = 129.
7. В альбоме 140 марок. Причем марок с животными на 67 меньше, чем марок с цветами. Сколько марок каждого вида в альбоме?
8. Три бригады собрали 40 ц картофеля. Первая собрала 14 ц, а вторая на 7 ц больше. Сколько центнеров картофеля собрала третья бригада?
9. Коля задумал число, увеличил его на 13, а затем результат уменьшил на 6 и получил число 12. Какое число задумал Коля?
10. (3 балла) Решите уравнение   576 – (129 + у) – 11 = 105.
11. (3 балла) Запишите наибольшее двузначное число и наименьшее четырехзначное. На сколько одно больше другого?
12. (5 баллов) Найдите число, если известно, что число которое меньше самого большого трехзначного числа на 342, больше его на 23.

Вариант № 2

1. Укажите какое из чисел меньше: 5286 и 5268.
2. Даны числа: 374, 74, 34, 743, 47 и 344. Расположите эти числа в порядке убывания.
3. Найдите:

а) разность чисел 89715 и 48987;
б) сумму чисел 56877 и 16384.

4. Вычислите: 595 + (324 – 65) – 784.
5. Проверьте, правильно ли выполнены действия:

а) 71571 – 52634 = 18947;
б) 26789 + 15357 = 42146.

6. Решите уравнение х – 874 = 129.
7. В коробке 44 карандаша. Причем цветных карандашей на 16 больше, чем простых. Сколько простых и цветных карандашей в коробке?
8. Три фермерских хозяйства засеяли 36 га пшеницей. Первое хозяйство отвело под посевы пшеницы 11 га, а второе на 3 га меньше. Какова площадь, отведенная третьим хозяйством под посевы пшеницы?
9. Аня задумала число, уменьшила его на 7, а затем результат увеличила на 16 и получила число 62. Какое число она задумала?
10. (3 балла) Решите уравнение  186 + (42 + х) – 71 = 215.
11. (3 балла) Запишите наименьшее двузначное число и наибольшее трехзначное четырехзначное. На сколько одно меньше другого?
12. (5 баллов) Найдите число, если известно, что число которое больше самого маленького трехзначного числа на 173, меньше его на 37.

Зачет №2. Умножение и деление натуральных чисел

Вариант № 1

1. Найдите:

а) частное двух чисел 51208 и 148;
б) произведение чисел 206 и 193.

2. Разложите число 56 на три множителя двумя различными способами.
3. Вычислите 10355 : (459 – 52•7).
4. Найдите значение выражения: 342 + 45•х, если х = 403.
5. Один спортсмен пробежал дистанцию в 54 км за 6 ч, а другой дистанцию 72 км за 9 ч. У кого из них скорость больше?
6. Найдите куб и квадрат числа 13.
7. Решите уравнение 75•у = 900.
8. Выполните деление с остатком: 34895 на 174.
9. Скорость поезда 68 км/ч, а скорость автомобиля на 24 км/ч больше. Какое расстояние может преодолеть каждый из этих видов транспорта за 3 ч?
10. (3 балла) Выполните действия 216•24 – 121•31 + 27•51.
11. (3 балла) Неизвестное число разделили на 8. В частном получили 17, а в остатке 4. Какое это число?
12. (5 баллов) Угадайте корень уравнения х•х – 24 = 1 и сделайте проверку.

Вариант № 2

1. Найдите:

а) частное двух чисел 51208 и 148;
б) произведение чисел 326 и 109.

2. Разложите число 48 на три множителя двумя различными способами.
3. Вычислите 3540 : (107 + 47•4).
4. Найдите значение выражения: 561 – 1246 : у, если у = 14.
5. Черепаха проползла за 8 ч 2 км 40 м, а ящерица пробежала – за 5 ч расстояние, равное 14 км. У кого из них скорость больше?
6. Найдите куб и квадрат числа 17.
7. Решите уравнение 34•х = 408.
8. Выполните деление с остатком: 64798 на 231.
9. Скорость самолета 860 км/ч, а скорость аэроплана 120 км/ч больше. Какое расстояние может преодолеть каждый из этих видов транспорта за 2 ч?
10. (3 балла) Выполните действия   354•46 – 37•115 + 171•23.
11. (3 балла) Неизвестное число разделили на 17. В частном получили 5, а в остатке 11. Какое это число?
12. (5 баллов) Угадайте корень уравнения х•х – 15 – 2 = 0 и сделайте проверку.

Зачет N№ 3. Формулы. Измерения площадей и объемов

Вариант № 1

1. Найдите значение выражения по формуле 3•х + 11 – 2•у, если х = 5, а у = 7.
2. Найдите путь s, если скорость v = 23 км/ч, а время t = 3ч.
3. Найдите ширину прямоугольника, если его площадь равна 72 см², а длина 12 см.
4. Найдите объем куба, если длина его ребра 5 см.
5. Длина игровой площадки, имеющей форму прямоугольника, в 3 раза больше ширины. Найдите площадь площадки, если ширина 12 м.
6. Длина прямоугольного параллелепипеда 6 см, ширина на 2 см меньше, а высота больше ширины на 5 см. Найдите объем прямоугольного параллелепипеда.
7. Начертите квадрат со стороной 6 см и разделите его на три равные части. Найдите площадь одной такой части и ее периметр. Во сколько раз площадь части квадрата меньше площади самого квадрата?
8. Вычислите:

а) 5 кг 45 г + 900 г – 1 кг 700 г;
б) 4 м 9 дм – 180 см + 16 дм 2 см.

9. Выполните действия: 368 + 7293 : ( 587– 158) • 13.
10. (3 балла) Куб некоторого числа равен 8, чему равен квадрат этого числа?
11. (3 балла) Найдите сторону квадрата, если его площадь равна площади прямоугольника со сторонами 3 см и 12 см.
12. (5 баллов) Неизвестное число разделили на 5. Получившееся частное умножили на 20, а полученное произведение разделили на 2. Как и во сколько раз изменилось это число?

Вариант № 2

1. Найдите значение выражения по формуле 15•х – 16 : а + 4, если х = 7, а = 8.
2. Найдите скорость v, если путь s = 135 км, а время t = 3 ч.
3. Найдите длину прямоугольника, если его площадь равна 48 см², а ширина 4 см.
4. Найдите объем куба, если длина его ребра 7 см.
5. Ширина парка, прямоугольной формы в городе N в 2 раза меньше длины этой площади. Найдите площадь парка, если длина парка 28 м.
6. Длина прямоугольного параллелепипеда 9 см, ширина на 4 см меньше, а высота меньше ширины на 3 см. Найдите объем прямоугольного параллелепипеда.
7. Начертите квадрат со стороной 4 см. разделите его на четыре равные части. Найдите периметр и площадь одной такой части. Во сколько раз площадь квадрата больше площади одной такой части?
8. Вычислите:

а) 6 т 7 ц – 3 т 8 ц + 1 ц;
б) 1 м 34 дм – 45 см + 4 м 8 дм 7 см.

9. Выполните действия: 502 – (214 + 458) : 16.
10. (3 балла) Квадрат некоторого числа равен 36, чему равен куб этого числа?
11. (3 балла) найдите площадь квадрата, если его площадь равна площади прямоугольника со сторонами 16 см и 4 см.
12. (5 баллов) Неизвестное число умножили на 60, затем разделили на 15, а потом умножили на 3. Как и во сколько раз изменилось данное число?

Зачет № 4. Обыкновенные дроби

Вариант № 1

1. Укажите две правильные и две неправильные дроби со знаменателем 13; с числителем 7.
2. Вместо звездочек поставьте числа так, чтобы было верным предложение:

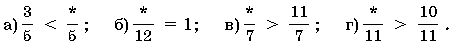
Выполните сложение (№ 3, 4):

3.
4. .

Выполните вычитание (№ 5, 6):

5.
6.

7. Столяр изготовил 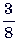заказа до обеда и 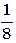заказа после обеда. Сколько ему осталось сделать деталей, если всего он должен был сделать 84 детали.

8.

а) Выделите целую часть из дроби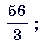
б) Запишите в виде неправильной дроби число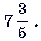

9. Рассказ и две повести занимают вместе 186 страниц. Один рассказ занимает 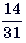книги, а повесть занимает – 86 страниц. Сколько страниц занимает второй рассказ?

10. (3 балла) Вычислите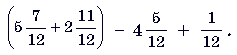 

11. (3 балла) Стороны треугольника соответственно равны 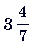cм, 5 см и 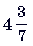см. Найдите периметр треугольника.

12. (5 баллов) Найдите число, 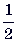которого равна 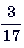от 51.

Вариант № 2

1. Укажите две правильные и две неправильные дроби со знаменателем 19; с числителем 8.
2. Вместо звездочек поставьте числа так, чтобы было верным предложение:

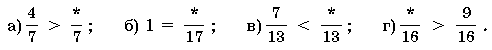
Выполните сложение (№ 3, 4):

3. 

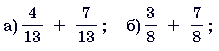
4. 

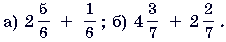
Выполните вычитание (№ 5, 6):

5. 

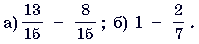
6.

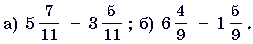
7. До полудня трактор вспахал 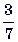  всей площади поля и 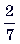после полудня. Сколько ему останется еще вспахать, если площадь всего поля – 84 га.

8. а) Выделите целую часть из дроби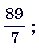 

б) Запишите в виде неправильной дроби число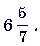

9. В парке растет 242 дерева – липы, березы и ели. Березы составляют всех деревьев, елей – 43. Сколько лип растет в парке?

10. (3 балла) Вычислите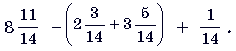

11. (3 балла) Стороны треугольника соответственно равны 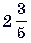см, 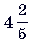см и 6 см. Найдите периметр треугольника.

12. (5 баллов) Найдите число, 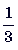  которого равна 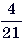от 42.

Зачет № 5. Сложение и вычитание десятичных дробей

Вариант № 1

1. Запишите в виде десятичной дроби число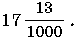

2. Сравните число:

а) 45,67 и 45,76; б) 9,2 и 9,099; в) 12,4 и 4,89.

3. Округлите число: а) 9,678 до сотых; б) 4,325 до десятых.

4. Выполните сложение: а) 45,18 + 6,2; б) 8,487 + 6,23.

5. Выполните вычитание: а) 7,89 – 4,51; б) 6,04 – 4,4.

6. Вычислите (2,24 + 7,15) – 2,83.

7. Решите уравнение 5,6 – х = 2,78.

8. Длина одного отрезка равна 14,3 см, а другой короче первого на 5,6 см. Какова длина второго отрезка?

9. Скорость теплохода по течению реки 62,8 км/ч. Собственная скорость теплохода 60,3 км/ч. Определите скорость теплохода против течения.

10. (3 балла) Найдите значение выражения  х – 3,25 – у + 6,2,   если х = 7, а у = 2,67.

11. (3 балла) Найдите периметр прямоугольника, если его длина равна 5,67 см, ширина на 2,39 см меньше. Ответ округлите до целых.

12. (5 баллов) Вместимость двух сосудов 12,8 л. Первый сосуд вмещает на 3,6 л больше, чем второй. Какова вместимость каждого сосуда?

Вариант № 2

1. Запишите в виде десятичной дроби число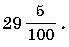

2. Сравните число:

а) 24,39 и 24,93; б) 6,3 и 6,043; в) 15,4 и 6,93.

3. Округлите число: а) 11,313 до десятых; б) 5,827 до сотых.

4. Выполните сложение: а) 24,36 + 6,4; б) 9,127 + 2,83.

5. Выполните вычитание: а) 6,73 – 3,42; б) 7,12 – 6,2.

6. Вычислите (7,13 – 3,48) + 4,54.

7. Решите уравнение х – 3,7 = 5,18.

8. Площадь одного квадрата равна 12,8 см², а площадь другого на 6,9 см² больше площади первого. Найдите площадь второго квадрата.

9. Скорость катера против течения реки 46,3 км/ч, а собственная скорость катера – 44,8 км/ч. Определите скорость катера по течению реки.

10. (3 балла) Найдите значение выражения  а + 7,65 – b – 3,4, если a = 13,2 а b = 2

11. (3 балла) Найдите периметр прямоугольника, если его ширина равна 3,42 дм, а длина на 3,39 дм больше. Ответ округлите до десятых.

12. (5 баллов) Два поля занимают площадь 156,8 га. Одно поле на 28,2 га больше другого. Найдите площадь каждого поля.

Зачет № 6. Умножение и деление десятичных дробей

Вариант № 1

1. Выполните умножение:

а) 2,1 • 7; б) 1,2 • 0,43; в) 13,9 • 0,01; г) 4,07 • 8,1.

2. Выполните деление:

а) 9, 16 : 16; б) 67 : 0,67; в) 7,5 : 0,5; г) 5,93 : 0,01.

3. Вычислите: 5,6•0,5 : 0,07 + 12,3.

Решите уравнения (№ 4, 5):

4. 0,53х – 3,4 = 7,2.

5. 32,1а – 19,6а = 1.

6. Найдите среднее арифметическое двух чисел:  12,3 и 4,6.

7. Скорость катера в стоячей воде 45,6 км/ч. Скорость течения 3,4 км/ч. Определите, какое расстояние пройдет катер, если он будет плыть 2 ч по течению и 3 ч против течения.

8. В грузовик погрузили 12 коробок по 12,4 кг в каждой и 14 коробок по 14,5 кг в каждой. Найдите массу груза.

9. Два пешехода вышли друг другу на встречу из городов, расстояние между которыми 44,8 км. Определите, через сколько часов они встретятся, если скорость одного пешехода 5,2 км/ч, а скорость другого на 0,8 км/ч больше.

10. (3 балла) Вычислите: 3 : 0,6 + 4,4 • (42,9 – 38,6).

11. (3 балла) С кондитерской фабрики отгрузили 20 коробок мармелада по 1,3 кг в коробке и 30 коробок по 1,1 кг мармелада. Сколько весит в среднем одна коробка?

12. (5 баллов) Среднее арифметическое двух чисел равно 9,46. Одно из них в 1,2 раза больше другого. Найдите оба числа.

Вариант № 2

1. Выполните умножение:  а) 5 • 4,7; б) 2,3 • 0,12; в) 15,68 • 0,1; г) 7,02 • ,34.

2. Выполните деление: а) 7,38 : 18; б) 74 : 0,74; в) 9,3 : 0,3; г) 4,26 : 0,01.

3. Вычислите: 4,6 • 0,5 : 0,25 – 6,14.

Решите уравнения (№ 4, 5):

4. 7,26 – 0,12у = 6,3

5. 9,14х – 7,89х = 1.

6. Найдите среднее арифметическое двух чисел  13,8 и 9,3.

7. Скорость моторной лодки по течению реки 36,5 км/ч, скорость течения 2,7 км/ч. определите, какое расстояние пройдет лодка, если будет плыть 2 ч против течения реки и 3 ч в озере.

8. Магазин продал 16 кг зефира по 62,5 р. за килограмм и 12 кг печенья по 38,7 р за килограмм. Сколько выручил магазин при продаже этих товаров?

9. Два мотоциклиста едут навстречу друг другу. Скорость первого 45,7 км/ч, а скорость второго на 5,5 км/ч больше скорости первого. Каково расстояние между двумя поселками, если встретились мотоциклисты через 4 ч.

10. (3 балла) Вычислите: 6 : 7,5 + (45,6 – 32,1)•6,4.

11. (3 балла) В магазин привезли 10 ящиков помидор по 3,7 кг в каждом и 40 ящиков по 6,5 кг в ящике. Сколько в среднем весит каждый ящик с помидорами?

12. (5 баллов) среднее арифметическое двух чисел равно 12,15. Одно число в 1,7 раза меньше другого. Найдите оба числа.

Зачет № 7. Проценты

Вариант № 1

1. Запишите дроби в виде процентов:  0,3; 0,01; 0,24 и 2,3.

2. Запишите проценты в виде десятичной дроби: 26%, 7%, 160%.

3. Найдите 5% от числа 240.

4. Из 76 м² общей площади квартиры кухня составляет 12%. Какова площадь кухни?

5. Содержание песка в земляной смеси составляет 20%. Какова масса земляной смеси, если песка в ней 34 кг.

6. Из углов 134°, 56°, 90°, 45°, 106° и 140° выберите тупые.

7. Постройте угол, градусная мера которого 48°.

8. Туристу нужно пройти 80 км, к концу первого дня он уже прошел 20 км. Сколько процентов всего пути преодолел турист?

9. Если к задуманному числу прибавить 30% от него, то получится число 39. Какое число задумали?

10. (3 балла) Вычислите: 7,3•2 – 10,8 : (6,8 – 5,6).

11. (3 балла) Что больше: 2% от 6 или 6% от 2?

12. (5 баллов) Найдите число, четверть которого равна 40% числа 55.

Вариант № 2

1. Запишите дроби в виде процентов:  0,02; 0,6; 3,05; 0,89.

2. Запишите проценты в виде десятичной дроби: 42%, 6% и 245%.

3. Найдите 12% от числа 560.

4. В сплаве находится медь содержание которой составляет 25%. Сколько меди в сплаве массой 76 кг?

5. Каков объем книги. Если в рассказе, который составляет 15% от общего числа страниц книги 12 страниц?

6. Из углов 13°, 90°, 180°, 123°, 29° и 89° выберите острые.

7. Постройте угол, градусная мера которого 128°.

8. Ученик решил 23 задач из 69. Сколько процентов от общего числа задач он решил?

9. Если от задуманного числа отнять 40% от него, то получится число 54. Какое число задумали?

10. (3 балла) Вычислите: 5,7 : 0,6 – ( 5,3 + 2,8)•2.

11. (3 балла) что больше: 15% от 40 или 40% от 10?

12. (5 баллов) Найдите число, треть которого составляет 50% числа 26.