ББК 65.050
ЗАДАЧА МАКСИМИЗАЦИИ ПРИБЫЛИ
А.С. Тирский, старший преподаватель кафедры «Естетственных и технических наук»,
А.С.Григорян, студент группы Эк 10 Олёкминский филиал
ФГБОУ ВПО Якутская ГСХА»,, г. Олёкминск
Как известно, математика в становлении всей экономической теории сыграла значительную роль . Практически все экономические процессы можно описать средствами математики, в частности функциональными методами. Более того , большинство экономических законов изначально выводились именно математическими способами. В наше время математика по прежнему шагает в ногу с экономикой ( равно как и с другими науками ) и упрощает и усовершенствует решение многих экономических задач. Одной из наиболее важных задач ,решаемых математическим способом является решение задачи на предельный анализ экономических процессов , те на нахождение наибольших или наименьших значений экономических величин(предельные задачи). Таких задач достаточно много и все они решаются средствами математического анализа ,а именно дифференциального исчисления . Следует заметить ,что решение таких задач может использоваться не только в теоретических исследованиях ,но и в профессиональной деятельности. Рассмотрим одну из таких задач, а именно задачу «Максимизации прибыли».
Пусть Q количество реализованного товара , R(Q) функция дохода. C(Q) функция затрат на производство товара. В реальности вид этих функций зависит в первую очередь от способа производства, организация инфраструктуры и.т.п . Прибыль от реализации произведенного товара задается формулой.П(Q)=R(Q)-C(Q).В микроэкономике известно утверждение : для ,того чтобы прибыль максимальной , необходимо , чтобы доход был максимальным , а издержки минимальными. Доказано , что в этом случае принцип можно записать в виде R'(Q)=C'(Q) . Действительно из необходимого условия экстремума для функции П(Q)=R(Q)-C(Q) следует, что 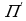 (Q)=0 откуда и получается основной принцип.
(Q)=0 откуда и получается основной принцип.
Приведем пример. Пусть R(Q)=100Q-Q2,C(Q)=Q3-37Q2+169Q+400
Тогда прибыль определяется формулойП(Q)=- Q3+36Q2-69Q-400
Производная прибыли равна: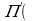 Q)=-3Q2+72Q-69. Получаем уравнение
Q)=-3Q2+72Q-69. Получаем уравнение
-3Q2+72Q-69=0 или Q2-24Q+23=0 . Решая это уравнение , получаем
Q=23 иQ=1. Исследуя на экстремум по одному из его достаточных условий, получаем: что 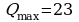 . Таким образом, чтобы прибыль был максимальным нужно производить 23 единицы продукта.
. Таким образом, чтобы прибыль был максимальным нужно производить 23 единицы продукта.
Литература:
-
Шипачев В.С. Задачник по высшей математике: Учебное пособие для вузов – М. Высшая школа, 2001.- 345с.
-
Шипачев В.С. Основы высшей математики: Учебное пособие для вузов – М: Высшая школа, 1998.- 380с.
-
Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах, в 2-х частях Ч.1,Ч.2.:Учебн. пособие для вузов – М.: Высшая школа, 1999.- 280с.







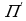 (Q)=0 откуда и получается основной принцип.
(Q)=0 откуда и получается основной принцип.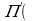 Q)=-3Q2+72Q-69. Получаем уравнение
Q)=-3Q2+72Q-69. Получаем уравнение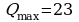 . Таким образом, чтобы прибыль был максимальным нужно производить 23 единицы продукта.
. Таким образом, чтобы прибыль был максимальным нужно производить 23 единицы продукта.



















