Задача одна - решений много

Задача одна – решений много

В преподавании математики большое место занимает решение задач. Успехи в обучении математики расцениваются главным образом по умению учащихся решать задачи. Такая высокая оценка умения решать задачи объясняется большим значением этого вида математической работы.

Действительно, решение задач оказывает большое влияние на умственное развитие детей, на развитие их мышления, внимания, воображения.

Решение задач имеет большое практическое значение: оно вооружает ученика умение производить различного рода расчета, часто встречающиеся в жизни.

На задачах выясняются и конкретизируются многие математические понятия.

Наконец, в решении задач находят свое практическое применение и закрепление, вычислительные навыки.

Для успешного решения задач от учащихся требуется известный уровень умственного развития, сообразительность, умение рассуждать, делать хотя бы простейшие умозаключения, требуется внимание и настойчивость в преодоление трудностей, более или менее развитое воображение. Но называя эти условия, нужно всегда помнить, что решение задач, в свою очередь, является самым мощным, самым действенным средством развития.

Умение решать задачи зависит от понимания учащимся связи и зависимости между теми величинами, которые даются в условии задачи. Установив зависимость между величинами, ученик должен произвести арифметические действия над числовыми значениями этих величин.

Правильно выбрав действия, ученик должен уметь правильно произвести вычисления. Неправильные вычисления приводят к невозможности решения задачи или неправильному ответу.

Задачи можно разделить на простые и составным.

На решение простых задач ученик уясняет, что такое задача и каковы ее элементы (условие, числовые данные, вопрос) на решение этих задач ученик учится понимать зависимость между величинами и правильно применять каждое арифметическое действие.

Составные задачи: когда учитель решает с учениками более сложную задачу, новую по своему содержанию или трудную для них в том или ином отношении, то он проводит учеников через следующие этапы:

• Условие усвоения задачи

• Разбор задачи

• Составление плана решения

• Решение ( вычисление)

Многие задачи решаются не одним, а несколькими способами; одни из этих способов кратки, легки, изящны, другие – трудны, громоздки. Важно сравнить и выбрать наиболее удобный.

Пример: Из двух городов одновременно вышли навстречу друг другу два поезда. Первый поезд идет со скоростью 45 км/ч , а второй – 50 км/ч. Встретились поезда через 5 часов, после начала движения. Какое расстояние между этими городами?

При первоначальном объяснении учитель дает такое решение:

I способ:

1) 45 км х 5 = 225 км прошел до встречи первый поезд

2) 50 км х 5 = 250 км прошел до встречи второй поезд

3)225 км +250 км = 475 км прошли оба поезда, то есть все расстояние между двумя городами.

Решив таким образом несколько задач, учитель показывает и другой, более краткий способ решения задач данного вида.

II способ:

1. 45 км + 50 км = 95 км проходят в час оба поезда

2. 95 км х 5 = 475 км прошли оба поезда за 5 часов

Решение одной и той же задачи двумя и более способами способствует более глубокому пониманию метода решения данной задачи: через различные варианты решения сильнее подчеркивается принцип решения.

Вообще же решение задач несколькими способами дает материал для сравнительной оценки, развивает инициативу учащихся, воспитывает самостоятельность их мышления, предприимчивость и смелость в поисках способов решения.

К различным способам решения, выдвигаемым самим учащимися в порядке их собственной инициативы, нужно относится весьма внимательно: нужно выслушать таких учеников, разбирать и оценивать их способы, поощряя тех, кто предлагает наиболее рациональные, остроумные способы.

Решим задачу несколькими способами:

ЗАДАЧА:

На гипотенузе АВ прямоугольного треугольника АВС построен квадрат АВDЕ в той полуплоскости от прямой АВ, которой не принадлежит треугольник АВС. Найдите расстояние от вершины С прямого угла до центра квадрата, если катеты ВС и АС имеют соответственно длины а и b.

РЕШЕНИЕ 1. ( ПО ТЕОРЕМЕ СИНУСОВ)

Теорема синусов:

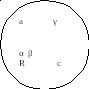
a / sin α = b / sin β = c / sin γ

Это отношение равно R,

b R – радиус описанной окружности

Пусть Q – центр построенного квадрата ( рис 1). Так как угол AQB прямой , то точка Q лежит на описанной около треугольника АВС окружности. Ее диаметром служит гипотенуза АВ. Из треугольника AQB по теореме синусов имеем:

СQ = АВ sin (α + 45º ) , где α – величина угла ВАС.

Далее получаем:

CQ = c ( sin α cos 45º + cos α sin 45º ) = (√2 / 2 ) c (a/c + b/c) = (a + b)/ √ 2

Где с = АВ

Итак, искомое расстояние CQ = (a + b)/ √ 2

РЕШЕНИЕ 2 ( ПО ТЕОРЕМЕ КОСИНУСОВ)

Т еорема косинусов:

b c² = a² + b² – 2ab cosγ

а γ

c

Из того же треугольника AQB по теореме косинусов находим:

СQ² = b² + AQ² – 2b AQ cos ( α + 45º )

Поскольку AQ² = ½ c² , то

CQ² = b² + ½ c² – 2b * с/√2 * √2/2 * ( b/c – a/c) = b² + ½ ( a² + b²) – b² + ab = ½ ( a + b)²

CQ = (a + b)/ √ 2

Р ЕШЕНИЕ 3 ( ПО ТЕОРЕМЕ ПТОЛЕМЕЯ)

Теорема Птолемея:

Во вписанном в окружность четырехугольнике сумма произведений длин противоположных сторон равно произведению длин диагоналей.

Поэтому для вписанного четырехугольника AQBC имеем:

a * AQ + b * BQ^’ = c * CQ

но AQ = BQ = c/√2 и следовательно,

( a + b) * c/√2 = c * CQ , откуда CQ = (a + b)/ √ 2

РЕШЕНИЕ 4 ( МЕТОДОМ ПЛОЩАДЕЙ)

Сумма площадей треугольников АВС и АВQ равна площади четырехугольника AQBC:

½ ab + ½ AQ² = ½ c CQ sinφ

Где φ – величина угла между прямыми АВ и СQ

Луч CQ есть биссектриса угла АСВ, так как вписанные углы ACQ и BCQопираются на равные дуги AQ и BQ

По теореме о внешнем угле треугольника φ = α + 45º

Теорема:

В нешний угол треугольника равен сумме двух внутренних углов, не смежных с ним:

β

δ = α + β

α δ

Подставив в предыдущее равенство AQ² = ½ ( a² + b²) и sinφ = √2/2 * ( a+ b)/c

( см.решение 1), получим:

ab + ½ ( a² + b²) = CQ * √2/2 (a + b)

CQ = (a + b)/ √ 2

РЕШЕНИЕ 5 ( МЕТОДОВ ГЕОМЕТРИЧЕСКИХ ПРЕОБРАЗОВАНИЙ)

Выполним поворот около центра Q квадрата на 90º:

П оворот:

Все точки фигуры поворачиваются на один и тот же угол вокруг одной и той же точки – центра поворота.

В А,

А А₁,

С С₁ ( Рис 2)

Так как 1АС₁ = 1 + 1АС₁ = 180º

Поэтому точки С, А, С₁ лежат на одной прямой.

В треугольнике СQС₁ угол СQС₁ прямой ( угол поворота)

СQ = C₁Q , CC₁ = CA + AC₁ = a + b

Следовательно из треугольника СQС₁ можно найти отношение СQ = sin 45º * CC₁

CQ = (a + b)/ √ 2

РЕШЕНИЕ 6 ( МЕТОДОМ КООРДИНАТ)

Примем прямые СА и СВ за оси Ох и Оу прямоугольной декартовой системе координат. Найдем координаты х, у точки Q. Она принадлежит биссектрисе угла АСВ ( см. решение 4) и равноудалена от точек А (b,0) и В(0,а).

Имеем систему:

х = у

( х – b)² + у² = х² + ( у – а)² ,

Откуда 2х( b – а) = b² – а²

Е сли а = b , то имеем уравнение х = у = ( а + b) /2

При а = b четырехугольник AQBC является квадратом и х = у = а, то есть координаты точки Q удовлетворяют прежнему решению.

По формуле расстояния между точками:

Расстояния между точками: АВ = √ ( х₁ – х₂ )² + (у₁ – у₂ )²

CQ = √ х² + у² = √ 2 ((а + b)/2)² = ( а +b)/ √2

CQ = (a + b)/ √ 2

РЕШЕНИЕ 7 ( ВЕКТОРНОЕ)

П оложим СА = b , СВ = а и выразим через эти векторы вектор CQ ( рис 1)

C Q = CA + AQ = b + ½ ( AB + AE) = b + ½ ( a – b) + ½ AE = ½ ( a + b) + ½ AE

П оложим АЕ = α а + βb , найдем коэффициенты α и β этого разложения, используя условия АЕ * АВ = 0 и |АЕ |= |АВ | , которые приводят к системе уравнений.

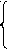
(α а + β b) ( a - b ) = 0

( α а + β b) ² = ( a - b )²

П 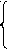оскольку ab = 0 , то эта система эквивалентна такой:

α а² - β b² =0

α ² а ² + β² b ² = a² + b ²

откуда α = b/a и β = a/b и, следовательно,

АЕ = b/a * a + a/b * b,

C Q = ½ ( a + b) + ½ ( b/a * a + a/b * b) = ½( ( ( a + b)/a) a + (( a + b)/b) b)

Наконец, CQ² = ½ ( a + b)² ,

CQ = (a + b)/ √ 2

РЕШЕНИЕ 8 ( МЕТОДОМ КОМПЛЕКСНЫХ ЧИСЕЛ

В ведем прямоугольную систему координат так же, как при решении 6. Тогда точки А, В,С будут иметь соответственно комплексные координаты b, ai, 0, причем а = а , b = b . при повороте на 90º вектор QB переходит в вектор QA . Этому повороту соответствует умножение на комплексное число i.

Поэтому имеем равенство: (ai – q )I = b – q , где q – комплексная координата точки Q.

Отсюда q = ( a + b) / ( 1 – i ).

Н аходим:

CQ² = q * q = (( a + b)/( 1 – i) ) * (( a + b) / ( 1 + i)) = ½ ( a + b )²

CQ = (a + b)/ √ 2

РЕШЕНИЕ 9 ( ЧИСТО ГЕОМЕТРИЧЕСКОЕ)

Опишем около квадрата другой квадрат со стороной а + b . Тогда искомое расстояние, очевидно, равно половине диагонали большого квадрата.

Суждение о простоте или трудности того или иного решения задачи в значительной мере субъективно. Оно существенно зависит о степени подготовленности, от уровня владения методами решения задач. При недостаточных навыках решений методом геометрических преобразований, векторным или координатным методом ученик скажет,, что первые четыре и решение 9 гораздо проще остальных. Однако решения 5 и 6 для подготовленного человека представляются ничуть не сложнее. Векторный метод для решения данной задачи оказался малоэффективным – решение 7 сложнее остальных. Но такая оценка векторного методавообще безусловна была не верна: решение многих других задач этим методом просты и изящны. Решение 8 с помощью комплексных чисел выглядит простым, однако требует специальной подготовки.

Сравнение различных решений одной задачи очень поучительною рекомендуется учителю накапливать такие решения и делать их сравнение при повторении материала.

Литература:

• Журнал «математика в школе»

№1 1992 г

№ 1 1990

№8 2004

№3 2002

• Методика преподавания арифметики