Задачи на построение

Шестнадцатое мая Классная работа Задачи на построение

Цель урока

• Повторить и систематизировать знания, умения и навыки по теме 2. Развивать творческую деятельность и пространственное представление 3.Интерес к предмету

Тест по теме «Окружность» Выберите правильный вариант ответа

1. Окружностью называется геометрическая фигура, которая

а) состоит из точек плоскости, расположенных на данном расстоянии от данной точки плоскости;

б) состоит из всех точек плоскости, расположенных на данном расстоянии от данной точки плоскости.

2. Центром окружности является

а) точка, от которой одинаково удалены некоторые точки;

б) точка, от которой одинаково удалены все точки окружности.

Тест ( продолжение)

3. Радиусом окружности называется

а) отрезок, соединяющий любую точку окружности с центром;

б) отрезок, соединяющий любую точку окружности с центром окружности.

4. Хордой окружности называется

а) отрезок, соединяющий две любые точки окружности;

б) отрезок, соединяющий две любые точки.

Тест(продолжение )

5. Диаметром окружности называется

а) прямая, проходящая через центр окружности;

б) хорда, проходящая через центр окружности.

1 - б

2 - б

3 - а

4 - а

5 - б

Оцени себя.

Если у тебя 5 верных ответов –

4 верных ответа –

3 верных ответа -

Задачи на построение

Это такие задачи, при

решении которых нужно построить геометрическую

фигуру, удовлетворяющую условию задачи с помощью циркуля и линейки без делений.

Основные задачи на построение

• Задача 1 . На данном луче от его начала отложить отрезок, равный данному.
• Задача 2 . Отложить от данного луча угол, равный данному.
• Задача 3. Построить биссектрису данного угла.
• Задача 4. Построить прямую, проходящую через данную точку и перпендикулярную к данной прямой.
• Задача 5. Построить середину данного отрезка.
• Задача 6. Построить прямую, проходящую через точку, не лежащую на данной прямой, и перпендикулярную этой прямой.

Схема решения задач на построение

• Анализ (рисунок искомой фигуры, устанавливающий связи между данными задачи и искомыми элементами; и план построения).
• Построение по намеченному плану.
• Доказательство, что данная фигура удовлетворяет условиям задачи.
• Исследование( при любых ли данных задача имеет решение, и если имеет, то сколько).

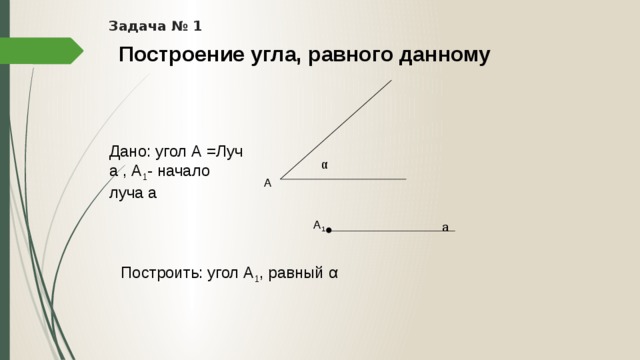
Задача № 1

Построение угла, равного данному

Дано: угол А = Луч а , А 1 - начало луча а

α

А

А 1

а

Построить: угол А 1 , равный α

Алгоритм построения

• 1.Построим окружность произвольного радиуса с центром в вершине данного угла А.
• 2.Радиусом АС проведём окружность с центром в точке А 1 – начальной точке луча а – и точку пересечения луча и окружности обозначим С 1.
• 3.Радиусом ВС проведём окружность с центром в точке С 1 и точку пересечения двух окружностей обозначим В 1 .
• 4.Проведём луч А 1 В 1. . Получим угол В 1 А 1 С 1, , равный данному. Равенство углов следует из равенства треугольников АВС и А 1 В 1 С 1. .

Задача № 2 Построение биссектрисы угла .

Дано: угол β

С

β

a

А

β

В

А

Построить биссектрису угла

Шаг 1

С

С

D

D

D

А

a

А

В

a

В

Шаг 3

Шаг 2

Описание построения задачи № 2

Шаг 1. Построим окружность произвольного радиуса с центром в точке А. Пусть В и С- точки пересечения этой окружности со сторонами угла.

Шаг 2. Радиусом АС проведём окружность с центром в точке В, тем же радиусом проведём окружность с центром в точке С. Точку пересечения этих окружностей обозначим D.

Шаг 3. Проведём луч АD, который и является биссектрисой данного угла А, равного β

Индивидуальная карточка

Индивидуальная карточка: Проверка

Домашнее задание: параграф 30-38 читать Построить тупоугольный треугольник и построить биссектрису тупого угла