"Задачи на построение сечений"

Задачи по теме «Сечения многогранников»

1. П остроить сечение прямоугольного параллелепипеда плоскостью, проходящей через три данные точки.

1. Ребра тет­ра­эд­ра равны 1. Най­ди­те пло­щадь се­че­ния, про­хо­дя­ще­го через се­ре­ди­ны че­ты­рех его ребер.

2. В пря­мо­уголь­ном па­рал­ле­ле­пи­пе­де ABCDA1B1C1D1 ребро AB=6, ребро AD=2√10, ребро AA1=4. Точка K — се­ре­ди­на ребра BB1. Най­ди­те пло­щадь се­че­ния, про­хо­дя­ще­го через точки A1, D1 и K.

3. В пря­мо­уголь­ном па­рал­ле­ле­пи­пе­де ABCDA1B1C1D1 из­вест­ны длины рёбер: AB=12, AD=9, AA1=32. Най­ди­те пло­щадь се­че­ния, про­хо­дя­ще­го через вер­ши­ны A, A1 и C.

4. В пря­мо­уголь­ном па­рал­ле­ле­пи­пе­де ABCDA1B1C1D1 из­вест­ны рёбра AB=8, AD=7, AA1=5. Точка W при­над­ле­жит ребру DD1 и делит его в от­но­ше­нии 1:4 счи­тая от вер­ши­ны D. Най­ди­те пло­щадь се­че­ния этого па­рал­ле­ле­пи­пе­да плос­ко­стью, про­хо­дя­щей через точки C, W и A1.

5. Точка E — се­ре­ди­на ребра CC1 куба ABCDA1B1C1D1. Най­ди­те пло­щадь се­че­ния куба плос­ко­стью A1BE, если ребра куба равны 2.

ПЛАН-КОНСПЕКТ УРОКА

«Задачи на построение сечений»

«Я слышу – я забываю, я вижу – я запоминаю, я делаю – я

усваиваю» (китайская мудрость)

Цели на урок:

• дидактические: формирование умения строить сечения тетраэдра и параллелепипеда, применять полученные знания для решения задач;

• развивающие: развитие умения формулировать гипотезы; развитие познавательного интереса, логического мышления, интеллектуальных способностей; формирование математической речи;

• воспитательные: воспитание у учащихся таких качеств личности как познавательная активность, самостоятельность, упорство в достижении цели, потребность в приобретении и углублении знаний, вырабатывать умение слушать и вести диалог, формирование эстетических навыков при оформлении записей в тетради.

Тип урока: урок открытия новых знаний

Структура урока:

1. Мотивационный этап.

2. Цели урока.

3. Этап изучения нового материала.

4. Этап закрепления нового материала (совместная деятельность учащихся)

5. Самостоятельная работа (индивидуальная работа учащихся)

6. Рефлексия.

7. Этап информации учащихся о домашнем задании.

Оборудование: компьютер, мультимедийный проектор, экран, презентация «Задачи на построение сечений», доска, мел, раздаточный материал с домашним заданием, индивидуальные карточки для рефлексии.

Замечание: данный урок проводится после изучения тем «Параллельность прямых и плоскостей» и «Перпендикулярность прямых и плоскостей».

ХОД УРОКА

1. Мотивационный этап. Цели урока.

Китайская мудрость гласит: «Я слышу – я забываю, я вижу – я запоминаю, я делаю – я усваиваю». Так давайте видеть и делать!!!

Для начала попробуем решить задачу.

• Каких знаний вам не хватает чтобы решить поставленную задачу?

• Какова, на ваш взгляд, тема над которой мы будем работать на уроке?

• Какие цели на урок вы можете перед собой поставить?

1. Этап изучения нового материала.

Для решения многих геометрических задач, полезно строить на рисунке их сечения различными плоскостями. Сегодня на уроке мы разберем основные приемы построения сечений тетраэдра и параллелепипеда. Уточним, сначала, что понимается под сечением.

• Как вы думаете, какие фигуры могут оказаться сечением тетраэдра? Параллелепипеда? От чего это зависит?

Прежде, чем приступить к построению сечений тетраэдра и параллелепипеда, следует иметь в виду

1. Соединять отрезком можно лишь точки, лежащие в плоскости одной грани.

1. Если секущая плоскость многогранника пересекает его параллельные грани по каким-либо отрезкам, то эти отрезки параллельны.

• Как вы думаете, почему?

• Сформулируйте свойство параллельных плоскостей.

1. Если секущая плоскость α проходит через прямую n, параллельную грани многогранника и пересекает эту грань, то линия пересечения плоскости α и этой грани параллельна прямой n.

Попробуем осознать то, что записали, отыскав ошибки в построении сечений.

1. Этап закрепления нового материала.

Итак, теоретическая часть урока подошла к концу, мы «увидели и запомнили», а теперь начинаем «делать и усваивать».

Задача 1.

• Является ли прямоугольник MNPQ квадратом? Докажите это самостоятельно.

Задача 2.

Задача 3.

Задача, с которой был начат урок.

1. Самостоятельная работа

Проверка с помощью документ-камеры двух любых работ (по одной из каждого варианта), обсуждение ошибок, если таковые были допущены, сравнение с решением, предложенным учителем (остановиться на вариантах записи решения, обсудить, что является ошибкой, какие могут быть недочеты).

1. Рефлексия «Оцени себя на уроке».

Учащимся дается индивидуальная карточка, в которой нужно подчеркнуть фразы, характеризующие работу ученика на уроке по трем направлениям. (Приложение 2)

1. Информация о домашнем задании (Приложение 1)

Решить задачи 1-4.

Индивидуальное дополнительное задание (для более подготовленных учащихся и тех, кто хочет попробовать свои силы при решении более сложных задач) – задачи 5,6.

Задачи на построение сечений

Курылева С.С., учитель математики

МОУ «Лицей №1» г. Воркуты

« Я слышу – я забываю,

я вижу – я запоминаю,

я делаю – я усваиваю»

(китайская мудрость)

Попробуем решить

В прямоугольном параллелепипеде ABCDA 1 B 1 C 1 D 1 ребро CD=2 , ребро BC=√5, ребро AA 1 =2 . Точка K – середина ребра DD 1 .

Найдите площадь сечения, проходящего через точки C, B и K.

Тема урока:

Задачи на

построение

сечений

Цели на урок:

• формирование умения строить сечения тетраэдра и параллелепипеда;

• формирование умения применять полученные знания при решения задач.

Секущая плоскость многогранника – любая плоскость, по обе стороны от которой находятся точки данного многогранника

Секущая плоскость пересекает грани многогранника по отрезкам. Многоугольник, сторонами которого являются эти отрезки называется сечением многогранника .

Сечения тетраэдра и параллелепипеда

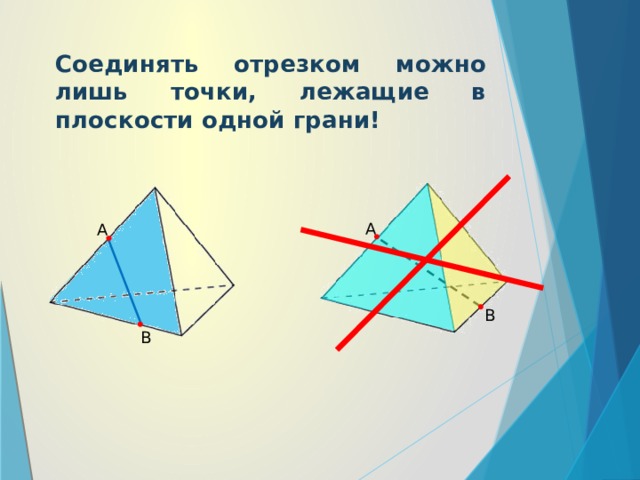
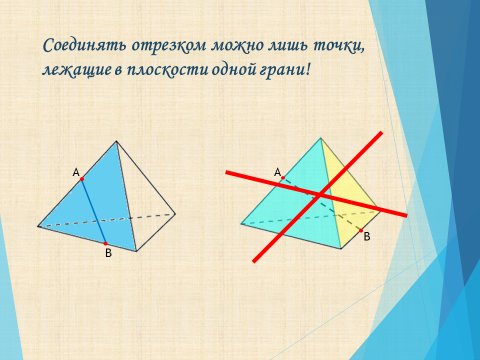
Соединять отрезком можно лишь точки, лежащие в плоскости одной грани!

А

А

В

В

Если секущая плоскость многогранника пересекает его параллельные грани по каким-либо отрезкам, то эти отрезки параллельны.

M

AB||CD

D

B

BM||CN

DM||AN

A

C

N

m||n m α∩(ABS)=m α B А n C" width="640"

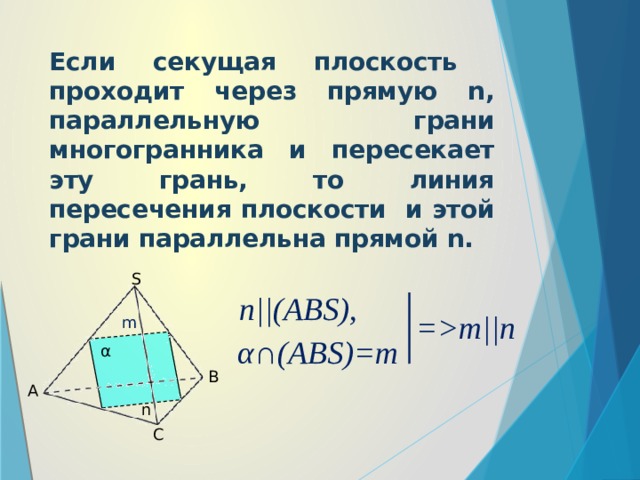
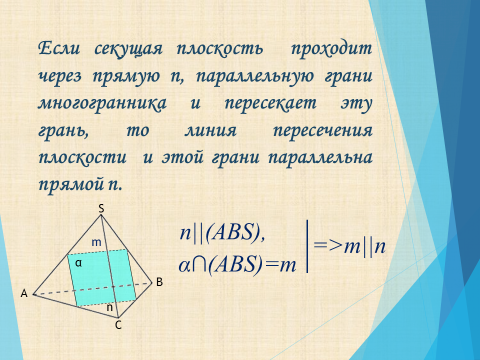
Если секущая плоскость проходит через прямую n, параллельную грани многогранника и пересекает эту грань, то линия пересечения плоскости и этой грани параллельна прямой n.

S

n||(ABS),

=m||n

m

α∩(ABS)=m

α

B

А

n

C

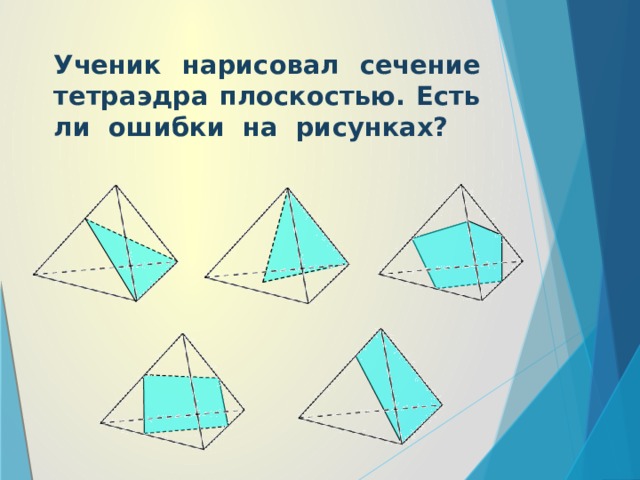
Ученик нарисовал сечение тетраэдра плоскостью. Есть ли ошибки на рисунках?

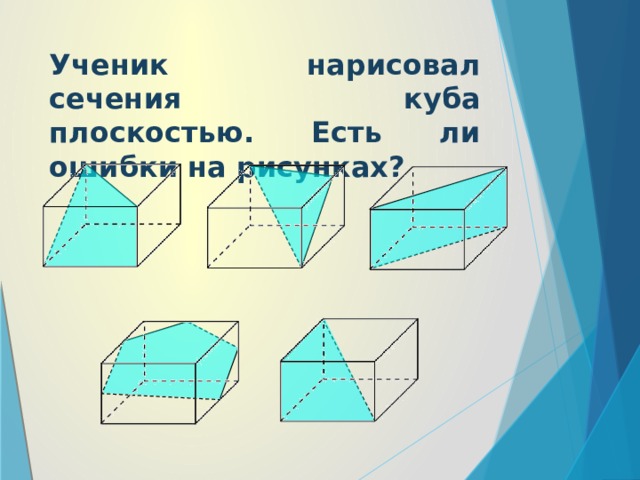
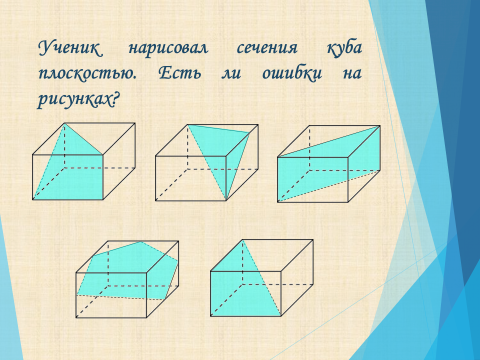
Ученик нарисовал сечения куба плоскостью. Есть ли ошибки на рисунках?

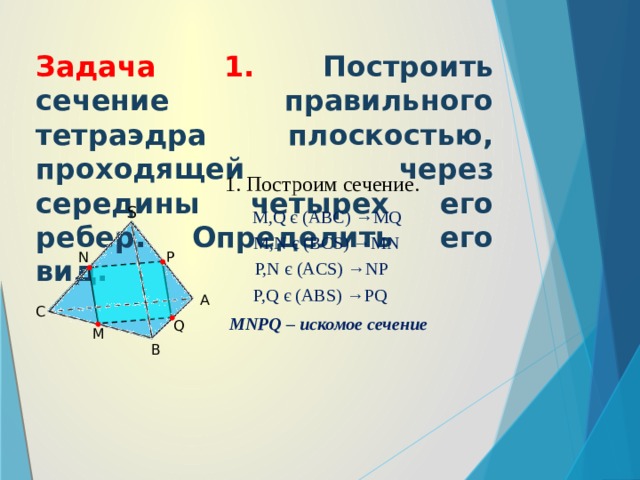
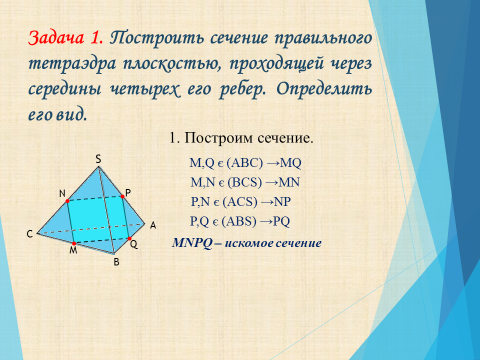
Задача 1. Построить сечение правильного тетраэдра плоскостью, проходящей через середины четырех его ребер. Определить его вид.

1. Построим сечение.

S

M,Q є (ABC) →MQ

M,N є (BCS) →MN

P

N

P,N є (ACS) →NP

P,Q є (ABS) →PQ

A

C

MNPQ – искомое сечение

Q

M

B

S

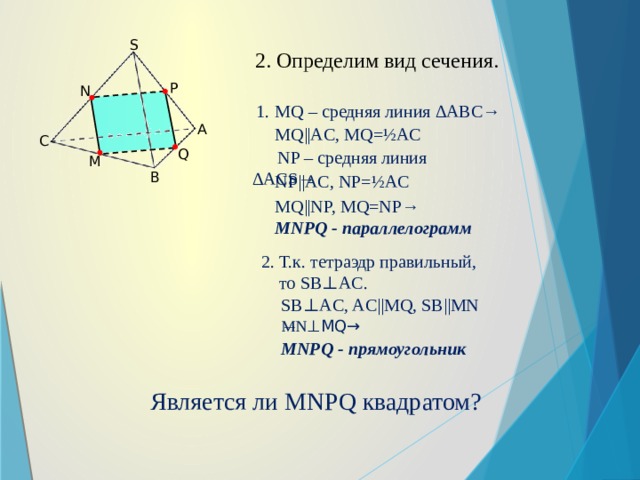
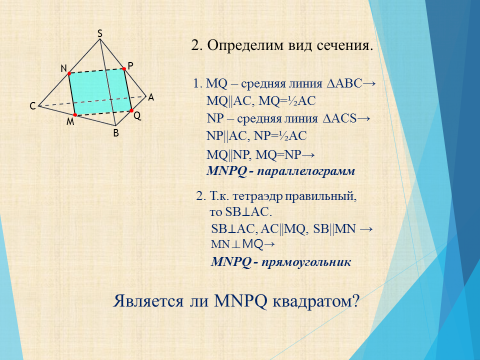
2. Определим вид сечения.

P

N

1. MQ – средняя линия ∆ABC→

A

MQ||AC, MQ=½AC

C

Q

NP – средняя линия ∆ACS→

M

B

NP||AC, NP=½AC

MQ||NP, MQ=NP→

MNPQ - параллелограмм

2. Т.к. тетраэдр правильный,

то SB⊥AC.

SB⊥AC, AC||MQ, SB||MN →

MN ⊥MQ→

MNPQ - прямоугольник

Является ли MNPQ квадратом?

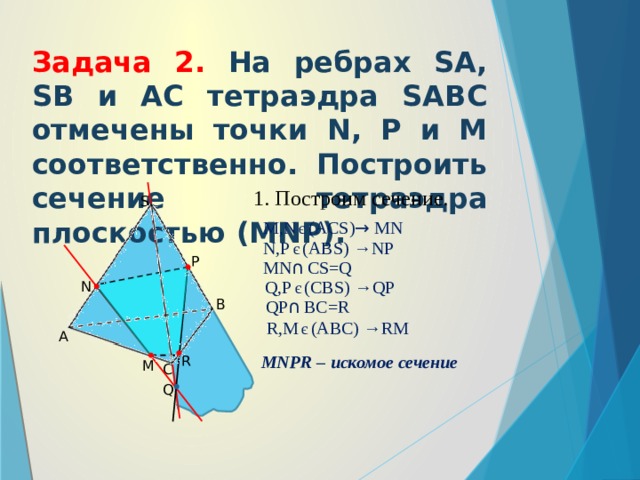
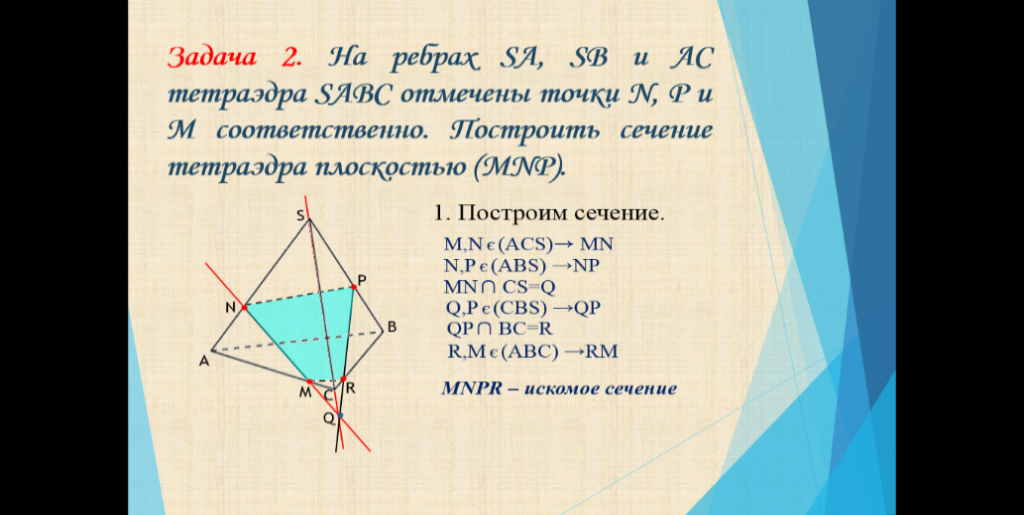
Задача 2. На ребрах SA, SB и AC тетраэдра SABC отмечены точки N, P и M соответственно. Построить сечение тетраэдра плоскостью (МNP).

1. Построим сечение.

S

M,N є (ACS) → MN

N,P є (ABS) →NP

P

MN ∩ CS=Q

Q,P є (CBS) →QP

N

QP ∩ BC=R

B

R,M є (ABC) →RM

A

MNPR – искомое сечение

R

M

C

Q

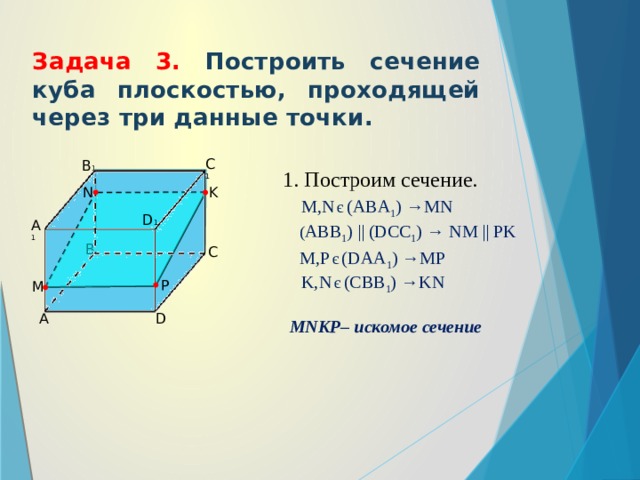
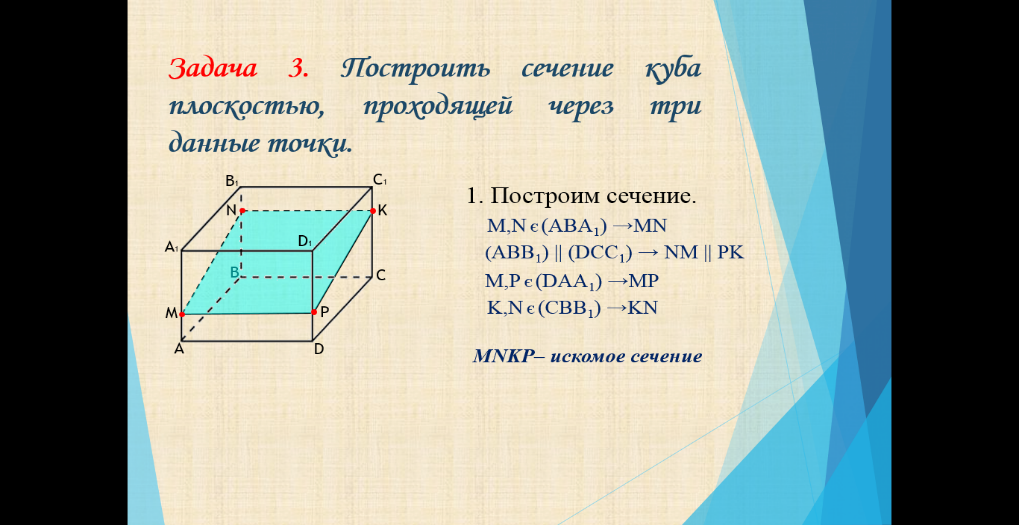
Задача 3. Построить сечение куба плоскостью, проходящей через три данные точки.

C 1

B 1

1. Построим сечение.

N

K

M,N є (ABA 1 ) →MN

D 1

A 1

( ABB 1 ) || (DCC 1 ) → NM || PK

B

C

M,P є (DAA 1 ) →MP

K,N є (CBB 1 ) →KN

P

M

A

D

MNKP– искомое сечение

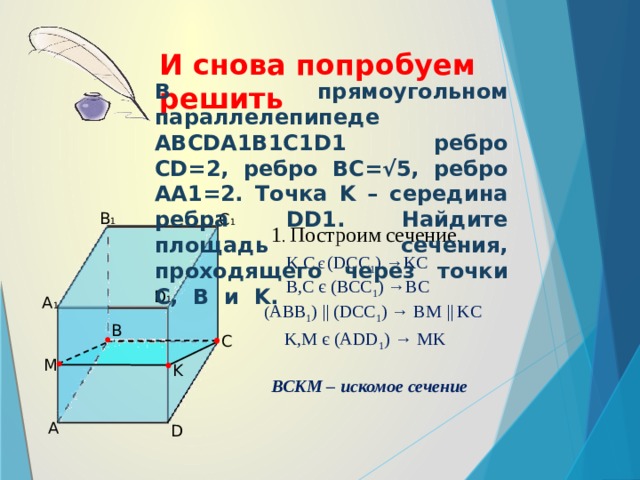
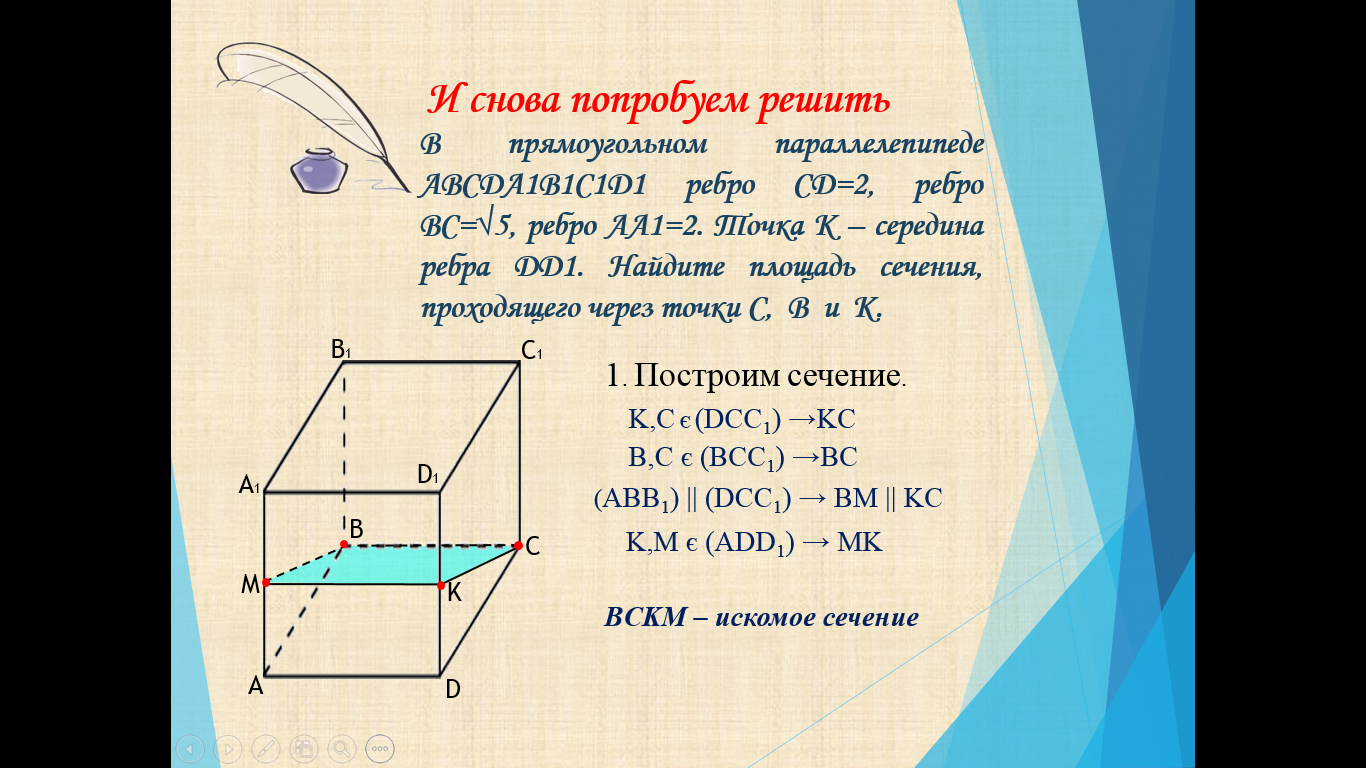
И снова попробуем решить

В прямоугольном параллелепипеде ABCDA1B1C1D1 ребро CD=2, ребро BC=√5, ребро AA1=2. Точка K – середина ребра DD1. Найдите площадь сечения, проходящего через точки C, B и K.

B 1

C 1

1 . Построим сечение .

K,C є (DCC 1 ) →KC

B,C є (BCC 1 ) →BC

D 1

A 1

( ABB 1 ) || (DCC 1 ) → BM || KC

B

K,M є (ADD 1 ) → MK

C

M

K

BCKM – искомое сечение

A

D

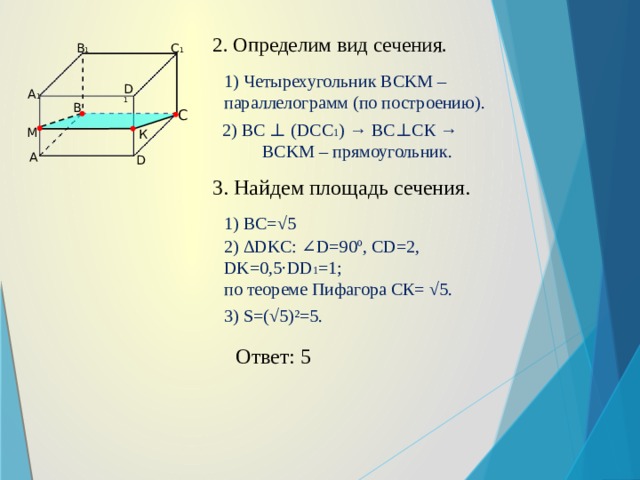
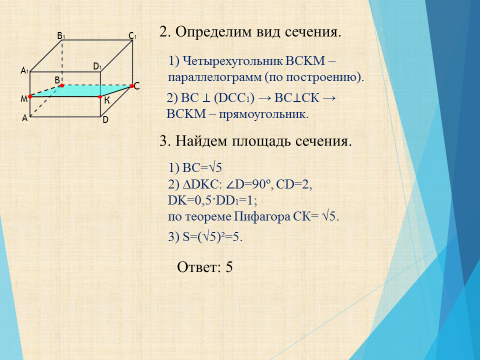
2. Определим вид сечения.

C 1

B 1

1) Четырехугольник BCKM – параллелограмм (по построению).

D 1

A 1

B

C

2) ВС ⊥ (DCC 1 ) → ВС⊥СК → BCKM – прямоугольник.

М

К

А

D

3. Найдем площадь сечения.

1) ВС=√5

2) ∆DKC: ∠D=90º, CD=2, DK=0,5·DD 1 =1;

по теореме Пифагора СК= √5.

3) S=(√5)²=5.

Ответ: 5

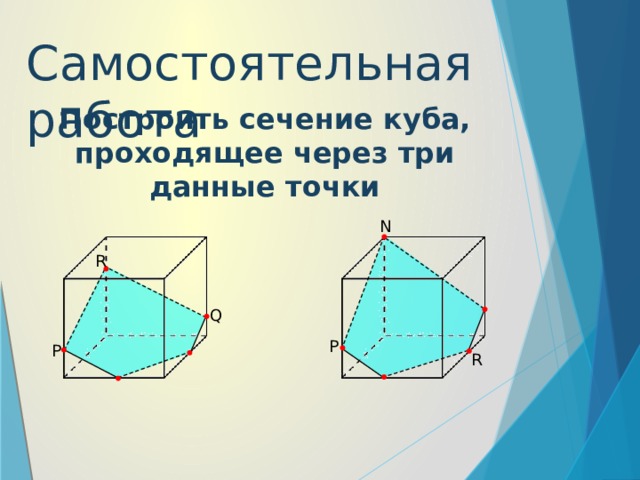
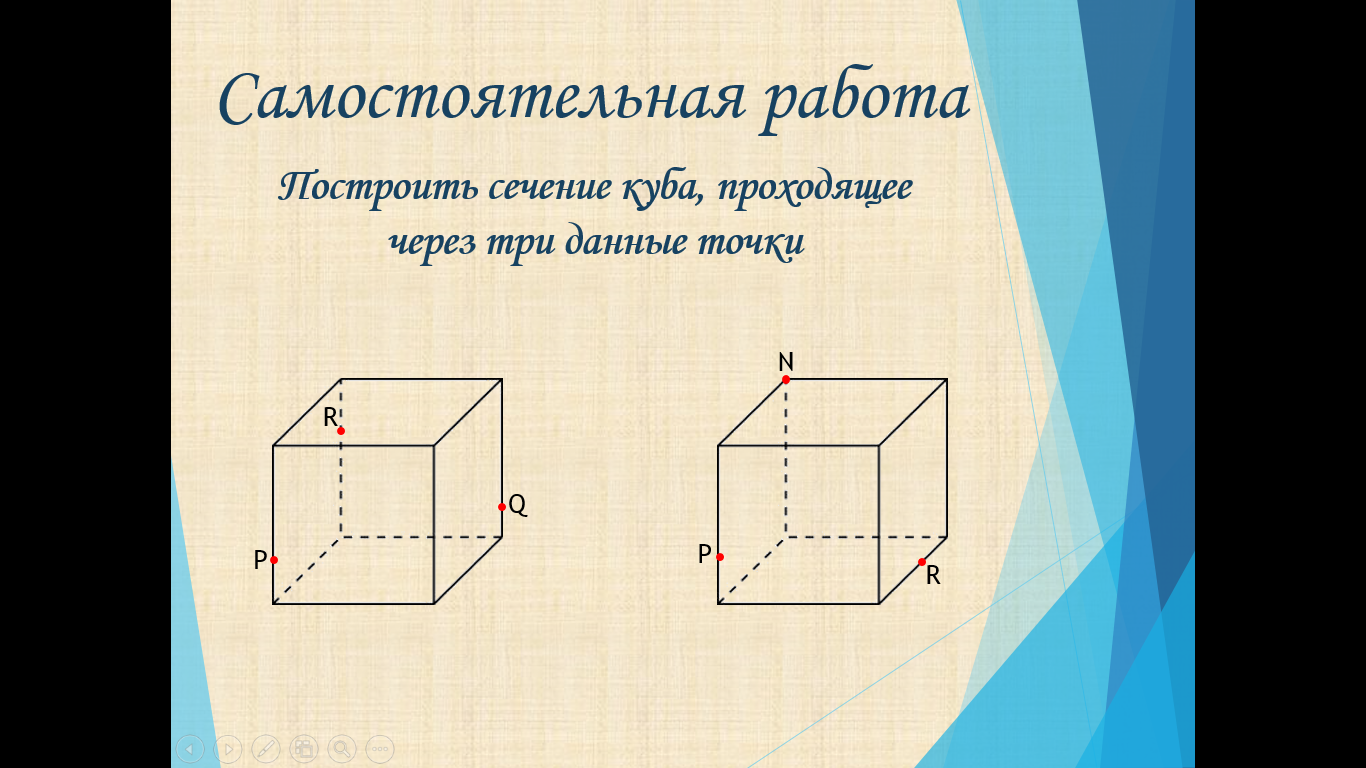
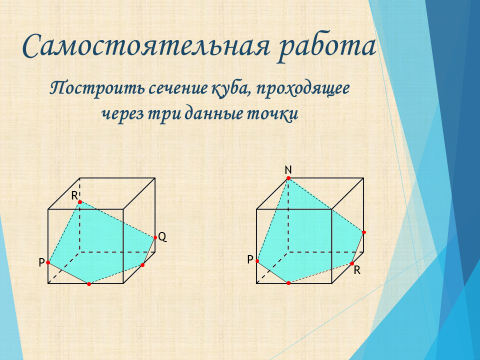
Самостоятельная работа

Построить сечение куба, проходящее через три данные точки

N

R

Q

P

P

R

Спасибо за урок!