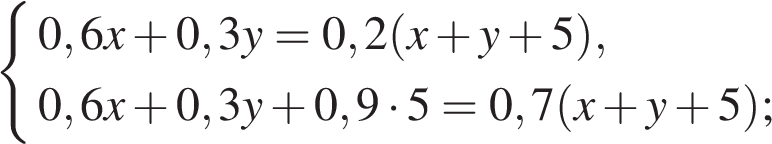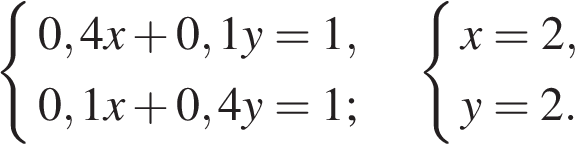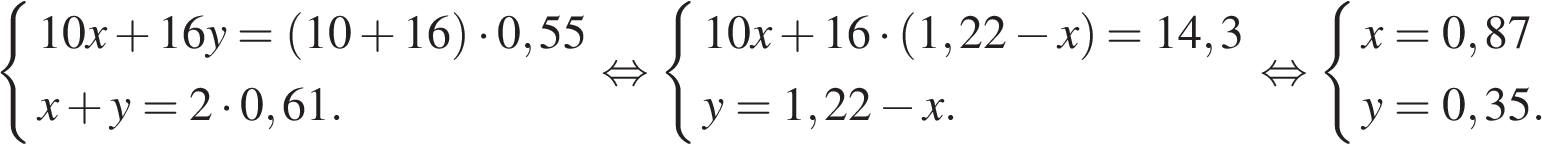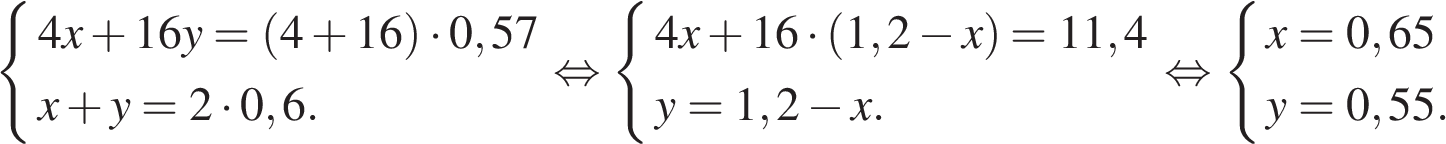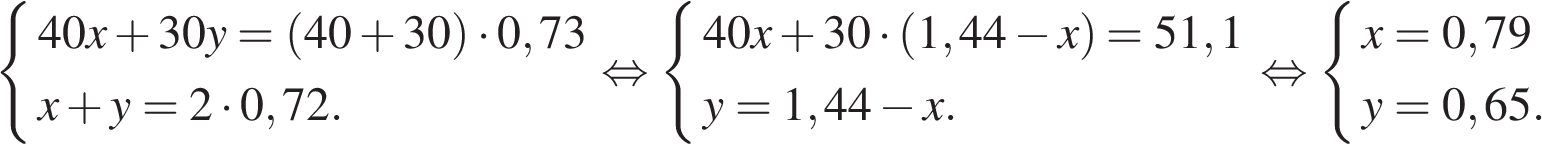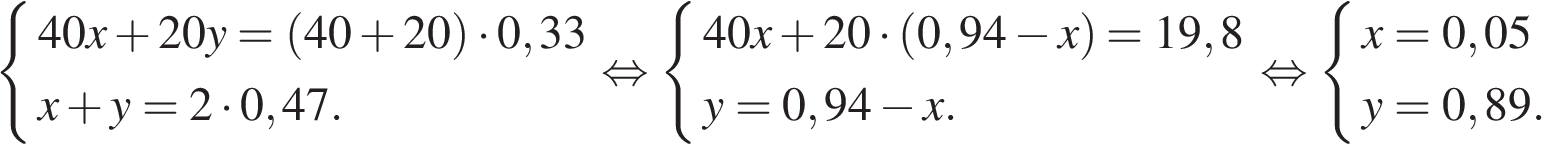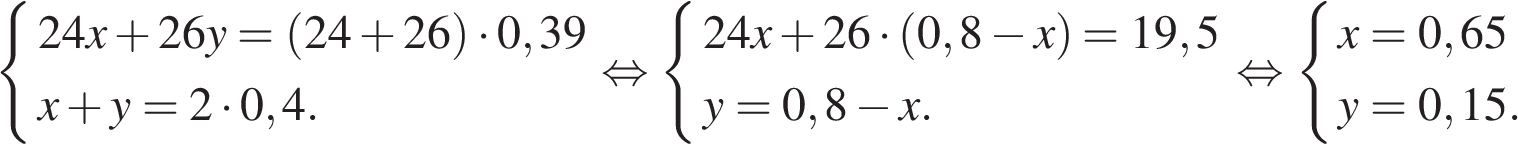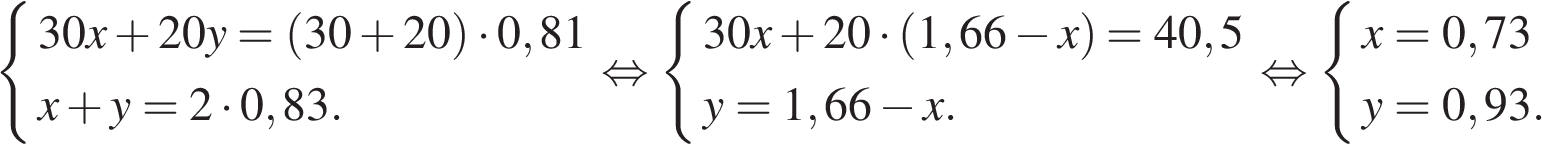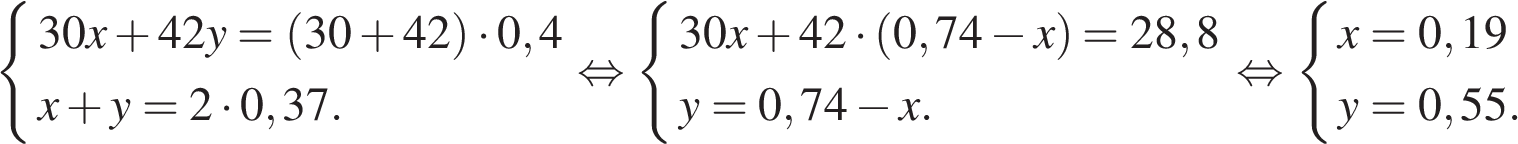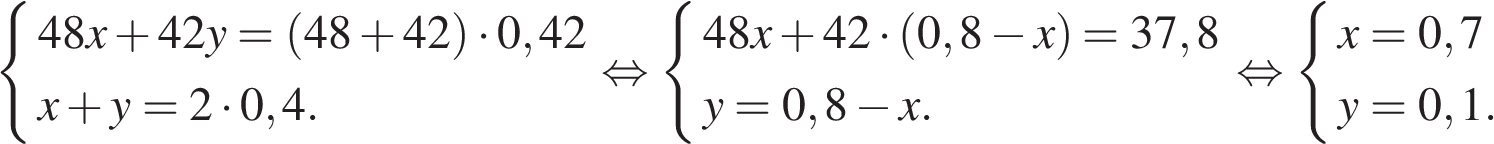Задачи на проценты, сплавы и смеси

Задачи на проценты, сплавы и смеси

1

Сме­шав 60%−ый и 30%−ый рас­тво­ры кис­ло­ты и до­ба­вив 5 кг чи­стой воды, по­лу­чи­ли 20%−ый рас­твор кис­ло­ты. Если бы вме­сто 5 кг воды до­ба­ви­ли 5 кг 90%−го рас­тво­ра той же кис­ло­ты, то по­лу­чи­ли бы 70%−ый рас­твор кис­ло­ты. Сколь­ко ки­ло­грам­мов 60%−го рас­тво­ра ис­поль­зо­ва­ли для по­лу­че­ния смеси?

2

Име­ет­ся два спла­ва с раз­ным со­дер­жа­ни­ем меди: в пер­вом со­дер­жит­ся 60%, а во вто­ром — 45% меди. В каком от­но­ше­нии надо взять пер­вый и вто­рой спла­вы, чтобы по­лу­чить из них новый сплав, со­дер­жа­щий 55% меди?

3

При сме­ши­ва­нии пер­во­го рас­тво­ра кис­ло­ты, кон­цен­тра­ция ко­то­ро­го 20%, и вто­ро­го рас­тво­ра этой же кис­ло­ты, кон­цен­тра­ция ко­то­ро­го 50%, по­лу­чи­ли рас­твор, со­дер­жа­щий 30% кис­ло­ты. В каком от­но­ше­нии были взяты пер­вый и вто­рой рас­тво­ры?

4

На пост главы ад­ми­ни­стра­ции го­ро­да пре­тен­до­ва­ло три кан­ди­да­та: Жу­равлёв, Зай­цев, Ива­нов. Во время вы­бо­ров за Ива­но­ва было от­да­но в 2 раза боль­ше го­ло­сов, чем за Жу­равлёва, а за Зай­це­ва — в 3 раза боль­ше, чем за Жу­равлёва и Ива­но­ва вме­сте. Сколь­ко про­цен­тов го­ло­сов было от­да­но за по­бе­ди­те­ля?

5

Пер­вый сплав со­дер­жит 5% меди, вто­рой — 13% меди. Масса вто­ро­го спла­ва боль­ше массы пер­во­го на 4 кг. Из этих двух спла­вов по­лу­чи­ли тре­тий сплав, со­дер­жа­щий 10% меди. Най­ди­те массу тре­тье­го спла­ва.

6

Све­жие фрук­ты со­дер­жат 80% воды, а вы­су­шен­ные — 28%. Сколь­ко сухих фрук­тов по­лу­чит­ся из 288 кг све­жих фрук­тов?

7

Сме­ша­ли не­ко­то­рое ко­ли­че­ство 10-про­цент­но­го рас­тво­ра­ не­ко­то­ро­го ве­ще­ства с таким же ко­ли­че­ством 12-про­цент­но­го рас­тво­ра ­это­го же ве­ще­ства. Сколь­ко про­цен­тов со­став­ля­ет кон­цен­тра­ция по­лу­чив­ше­го­ся рас­тво­ра?

8

Све­жие фрук­ты со­дер­жат 86 % воды, а вы­су­шен­ные — 23 %. Сколь­ко тре­бу­ет­ся све­жих фрук­тов для при­го­тов­ле­ния 72 кг вы­су­шен­ных фрук­тов?

9

Име­ют­ся два со­су­да, со­дер­жа­щие 10 кг и 16 кг рас­тво­ра кис­ло­ты раз­лич­ной кон­цен­тра­ции. Если их слить вме­сте, то по­лу­чит­ся рас­твор, со­дер­жа­щий 55% кис­ло­ты. Если же слить рав­ные массы этих рас­тво­ров, то по­лу­чен­ный рас­твор будет со­дер­жать 61% кис­ло­ты. Сколь­ко ки­ло­грам­мов кис­ло­ты со­дер­жит­ся в пер­вом рас­тво­ре?

10

Име­ют­ся два со­су­да, со­дер­жа­щие 4 кг и 16 кг рас­тво­ра кис­ло­ты раз­лич­ной кон­цен­тра­ции. Если их слить вме­сте, то по­лу­чит­ся рас­твор, со­дер­жа­щий 57% кис­ло­ты. Если же слить рав­ные массы этих рас­тво­ров, то по­лу­чен­ный рас­твор будет со­дер­жать 60% кис­ло­ты. Сколь­ко ки­ло­грам­мов кис­ло­ты со­дер­жит­ся в пер­вом рас­тво­ре?

11

Име­ют­ся два со­су­да, со­дер­жа­щие 40 кг и 30 кг рас­тво­ра кис­ло­ты раз­лич­ной кон­цен­тра­ции. Если их слить вме­сте, то по­лу­чим рас­твор, со­дер­жа­щий 73% кис­ло­ты. Если же слить рав­ные массы этих рас­тво­ров, то по­лу­чен­ный рас­твор будет со­дер­жать 72% кис­ло­ты. Сколь­ко ки­ло­грам­мов кис­ло­ты со­дер­жит­ся во вто­ром рас­тво­ре?

12

Име­ют­ся два со­су­да, со­дер­жа­щие 40 кг и 20 кг рас­тво­ра кис­ло­ты раз­лич­ной кон­цен­тра­ции. Если их слить вме­сте, то по­лу­чит­ся рас­твор, со­дер­жа­щий 33% кис­ло­ты. Если же слить рав­ные массы этих рас­тво­ров, то по­лу­чен­ный рас­твор будет со­дер­жать 47% кис­ло­ты. Сколь­ко ки­ло­грам­мов кис­ло­ты со­дер­жит­ся в пер­вом рас­тво­ре?

13

Име­ют­ся два со­су­да, со­дер­жа­щие 24 кг и 26 кг рас­тво­ра кис­ло­ты раз­лич­ной кон­цен­тра­ции. Если их слить вме­сте, то по­лу­чит­ся рас­твор, со­дер­жа­щий 39% кис­ло­ты. Если же слить рав­ные массы этих рас­тво­ров, то по­лу­чен­ный рас­твор будет со­дер­жать 40% кис­ло­ты. Сколь­ко ки­ло­грам­мов кис­ло­ты со­дер­жит­ся в пер­вом рас­тво­ре?

14

Име­ют­ся два со­су­да, со­дер­жа­щие 30 кг и 20 кг рас­тво­ра кис­ло­ты раз­лич­ной кон­цен­тра­ции. Если их слить вме­сте, то по­лу­чим рас­твор, со­дер­жа­щий 81% кис­ло­ты. Если же слить рав­ные массы этих рас­тво­ров, то по­лу­чен­ный рас­твор будет со­дер­жать 83% кис­ло­ты. Сколь­ко ки­ло­грам­мов кис­ло­ты со­дер­жит­ся во вто­ром рас­тво­ре?

15

Име­ют­ся два со­су­да, со­дер­жа­щие 22 кг и 18 кг рас­тво­ра кис­ло­ты раз­лич­ной кон­цен­тра­ции. Если их слить вме­сте, то по­лу­чит­ся рас­твор, со­дер­жа­щий 32% кис­ло­ты. Если же слить рав­ные массы этих рас­тво­ров, то по­лу­чен­ный рас­твор будет со­дер­жать 30% кис­ло­ты. Сколь­ко ки­ло­грам­мов кис­ло­ты со­дер­жит­ся в пер­вом рас­тво­ре?

16

Име­ют­ся два со­су­да, со­дер­жа­щие 30 кг и 42 кг рас­тво­ра кис­ло­ты раз­лич­ной кон­цен­тра­ции. Если их слить вме­сте, то по­лу­чим рас­твор, со­дер­жа­щий 40% кис­ло­ты. Если же слить рав­ные массы этих рас­тво­ров, то по­лу­чен­ный рас­твор будет со­дер­жать 37% кис­ло­ты. Сколь­ко ки­ло­грам­мов кис­ло­ты со­дер­жит­ся во вто­ром рас­тво­ре?

17

Име­ют­ся два со­су­да, со­дер­жа­щие 48 кг и 42 кг рас­тво­ра кис­ло­ты раз­лич­ной кон­цен­тра­ции. Если их слить вме­сте, то по­лу­чим рас­твор, со­дер­жа­щий 42% кис­ло­ты. Если же слить рав­ные массы этих рас­тво­ров, то по­лу­чен­ный рас­твор будет со­дер­жать 40% кис­ло­ты. Сколь­ко ки­ло­грам­мов кис­ло­ты со­дер­жит­ся во вто­ром рас­тво­ре?

18

Све­жие фрук­ты со­дер­жат 88 % воды, а вы­су­шен­ные — 30 %. Сколь­ко тре­бу­ет­ся све­жих фрук­тов для при­го­тов­ле­ния 6 кг вы­су­шен­ных фрук­тов?

19

Сме­ша­ли не­ко­то­рое ко­ли­че­ство 21-про­цент­но­го рас­тво­ра­ не­ко­то­ро­го ве­ще­ства с таким же ко­ли­че­ством 95-про­цент­но­го рас­тво­ра ­это­го же ве­ще­ства. Сколь­ко про­цен­тов со­став­ля­ет кон­цен­тра­ция по­лу­чив­ше­го­ся рас­тво­ра?

20

Све­жие фрук­ты со­дер­жат 93% воды, а вы­су­шен­ные — 16%. Сколь­ко сухих фрук­тов по­лу­чит­ся из 252 кг све­жих фрук­тов?

Задачи на проценты, сплавы и смеси

1. Сме­шав 60%−ый и 30%−ый рас­тво­ры кис­ло­ты и до­ба­вив 5 кг чи­стой воды, по­лу­чи­ли 20%−ый рас­твор кис­ло­ты. Если бы вме­сто 5 кг воды до­ба­ви­ли 5 кг 90%−го рас­тво­ра той же кис­ло­ты, то по­лу­чи­ли бы 70%−ый рас­твор кис­ло­ты. Сколь­ко ки­ло­грам­мов 60%−го рас­тво­ра ис­поль­зо­ва­ли для по­лу­че­ния смеси?

Ре­ше­ние.

Пусть 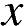  кг и   кг — массы пер­во­го и вто­ро­го рас­тво­ров, взя­тые при сме­ши­ва­нии. Тогда 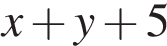  кг — масса по­лу­чен­но­го рас­тво­ра, со­дер­жа­ще­го   кг кис­ло­ты. Кон­цен­тра­ция кис­ло­ты в по­лу­чен­ном рас­тво­ре 20 %, от­ку­да

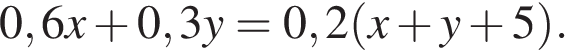
Решим си­сте­му двух по­лу­чен­ных урав­не­ний:

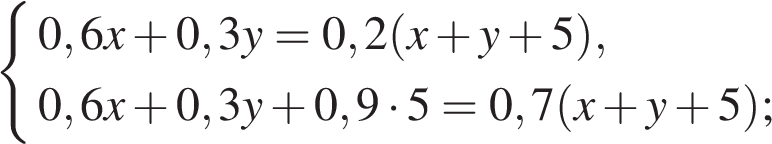
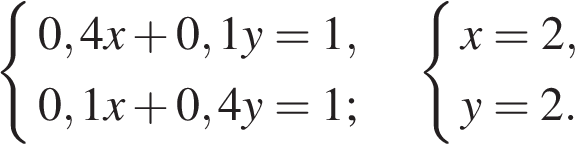
За­ме­ча­ние. Ре­ше­ние можно сде­лать не­сколь­ко проще, если за­ме­тить, что из по­лу­чен­ных урав­не­ний сле­ду­ет:  , от­ку­да  . Пер­вое урав­не­ние при­ни­ма­ет вид 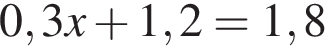 , от­ку­да  .

Ответ: 2 кг.

2. Име­ет­ся два спла­ва с раз­ным со­дер­жа­ни­ем меди: в пер­вом со­дер­жит­ся 60%, а во вто­ром — 45% меди. В каком от­но­ше­нии надо взять пер­вый и вто­рой спла­вы, чтобы по­лу­чить из них новый сплав, со­дер­жа­щий 55% меди?

Ре­ше­ние.

Пусть пер­вый сплав взят в ко­ли­че­стве x кг, тогда он будет со­дер­жать 0,6x кг меди, а вто­рой сплав взят в ко­ли­че­стве y кг, тогда он будет со­дер­жать 0,45y кг меди. Со­еди­нив два этих спла­ва, по­лу­чим сплав меди мас­сой x + y, по усло­вию за­да­чи он дол­жен со­дер­жать 0,55(x + y) меди. Сле­до­ва­тель­но, можно со­ста­вить урав­не­ние:

Вы­ра­зим x через y:

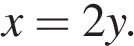
Сле­до­ва­тель­но, от­но­ше­ние, в ко­то­ром нужно взять спла­вы:

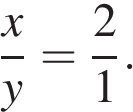
Ответ: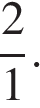 

3. При сме­ши­ва­нии пер­во­го рас­тво­ра кис­ло­ты, кон­цен­тра­ция ко­то­ро­го 20%, и вто­ро­го рас­тво­ра этой же кис­ло­ты, кон­цен­тра­ция ко­то­ро­го 50%, по­лу­чи­ли рас­твор, со­дер­жа­щий 30% кис­ло­ты. В каком от­но­ше­нии были взяты пер­вый и вто­рой рас­тво­ры?

Ре­ше­ние.

Пусть пер­вый рас­твор взят в ко­ли­че­стве 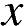  грамм, тогда он со­дер­жит 0,2 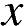 грамм чи­стой кис­ло­ты, а вто­рой рас­твор взят в ко­ли­че­стве   грамм, тогда он со­дер­жит 0,5  грамм чи­стой кис­ло­ты. При сме­ши­ва­нии двух этих рас­тво­ров по­лу­чит­ся рас­твор мас­сой 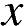  +   грамм, по усло­вию за­да­чи, он со­дер­жит 0,3(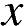  +  ) чи­стой кис­ло­ты. Сле­до­ва­тель­но, можно со­ста­вить урав­не­ние:

Вы­ра­зим 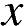  через  :  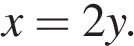 Сле­до­ва­тель­но, от­но­ше­ние, в ко­то­ром были взяты рас­тво­ры: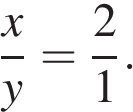 

Ответ: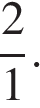 

4. На пост главы ад­ми­ни­стра­ции го­ро­да пре­тен­до­ва­ло три кан­ди­да­та: Жу­равлёв, Зай­цев, Ива­нов. Во время вы­бо­ров за Ива­но­ва было от­да­но в 2 раза боль­ше го­ло­сов, чем за Жу­равлёва, а за Зай­це­ва — в 3 раза боль­ше, чем за Жу­равлёва и Ива­но­ва вме­сте. Сколь­ко про­цен­тов го­ло­сов было от­да­но за по­бе­ди­те­ля?

Ре­ше­ние.

За­ме­тим, что по­бе­ди­те­лем на вы­бо­рах ока­жет­ся Зай­цев. Пусть ко­ли­че­ство го­ло­сов, от­дан­ных за Зай­це­ва равно 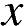 . Тогда за Жу­равлёва и Ива­но­ва вме­сте от­да­ли  . Про­цент го­ло­сов, от­дан­ных за Зай­це­ва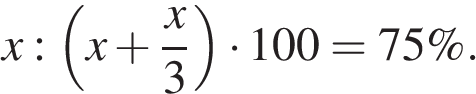  

Ответ: 75%.

5. Пер­вый сплав со­дер­жит 5% меди, вто­рой — 13% меди. Масса вто­ро­го спла­ва боль­ше массы пер­во­го на 4 кг. Из этих двух спла­вов по­лу­чи­ли тре­тий сплав, со­дер­жа­щий 10% меди. Най­ди­те массу тре­тье­го спла­ва.

Ре­ше­ние.

Пусть масса пер­во­го спла­ва x кг. Тогда масса вто­ро­го спла­ва (x + 4) кг, а тре­тье­го — (2x + 4) кг. В пер­вом спла­ве со­дер­жит­ся 0,05x кг меди, а во вто­ром — 0,13(x + 4) кг. По­сколь­ку в тре­тьем спла­ве со­дер­жит­ся 0,1(2x + 4) кг меди, со­ста­вим и решим урав­не­ние:

От­ку­да 

Масса тре­тье­го спла­ва равна 16 кг.

Ответ:16 кг.

6. Све­жие фрук­ты со­дер­жат 80% воды, а вы­су­шен­ные — 28%. Сколь­ко сухих фрук­тов по­лу­чит­ся из 288 кг све­жих фрук­тов?

Ре­ше­ние.

Све­жие фрук­ты со­дер­жат 20% пи­та­тель­но­го ве­ще­ства, а вы­су­шен­ные — 72%. В 288 кг све­жих фрук­тов со­дер­жит­ся 0,2 · 288 = 57,6 кг пи­та­тель­но­го ве­ще­ства. Такое ко­ли­че­ство пи­та­тель­но­го ве­ще­ства будет со­дер­жать­ся в 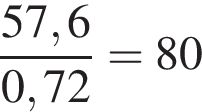  кг вы­су­шен­ных фрук­тов.

Ответ: 80.

Ответ: 80

7. Сме­ша­ли не­ко­то­рое ко­ли­че­ство 10-про­цент­но­го рас­тво­ра­ не­ко­то­ро­го ве­ще­ства с таким же ко­ли­че­ством 12-про­цент­но­го рас­тво­ра ­это­го же ве­ще­ства. Сколь­ко про­цен­тов со­став­ля­ет кон­цен­тра­ция по­лу­чив­ше­го­ся рас­тво­ра?

Ре­ше­ние.

Пусть взяли 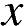  г 10-про­цент­но­го рас­тво­ра, тогда взяли и  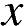 г 12-про­цент­но­го рас­тво­ра. Кон­цен­тра­ция рас­тво­ра — масса ве­ще­ства, раз­делённая на массу всего рас­тво­ра. В пер­вом рас­тво­ре со­дер­жит­ся  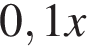 г, а во вто­ром —  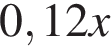 г Кон­цен­тра­ция по­лу­чив­ше­го­ся рас­тво­ра равна  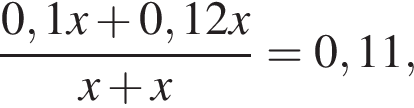 или 11%.

Ответ: 11%.

8. Све­жие фрук­ты со­дер­жат 86 % воды, а вы­су­шен­ные — 23 %. Сколь­ко тре­бу­ет­ся све­жих фрук­тов для при­го­тов­ле­ния 72 кг вы­су­шен­ных фрук­тов?

Ре­ше­ние.

За­ме­тим, что сухая часть све­жих фрук­тов со­став­ля­ет 14%, а вы­су­шен­ных — 77%. Зна­чит, для при­го­тов­ле­ния 72 кг вы­су­шен­ных фрук­тов тре­бу­ет­ся 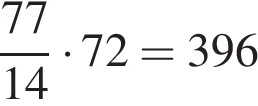  кг све­жих.

Ответ: 396 кг.

9. Име­ют­ся два со­су­да, со­дер­жа­щие 10 кг и 16 кг рас­тво­ра кис­ло­ты раз­лич­ной кон­цен­тра­ции. Если их слить вме­сте, то по­лу­чит­ся рас­твор, со­дер­жа­щий 55% кис­ло­ты. Если же слить рав­ные массы этих рас­тво­ров, то по­лу­чен­ный рас­твор будет со­дер­жать 61% кис­ло­ты. Сколь­ко ки­ло­грам­мов кис­ло­ты со­дер­жит­ся в пер­вом рас­тво­ре?

Ре­ше­ние.

Пусть кон­цен­тра­ция пер­во­го рас­тво­ра — х, кон­цен­тра­ция вто­ро­го рас­тво­ра — y. Со­ста­вим си­сте­му урав­не­ний со­глас­но усло­вию за­да­чи:

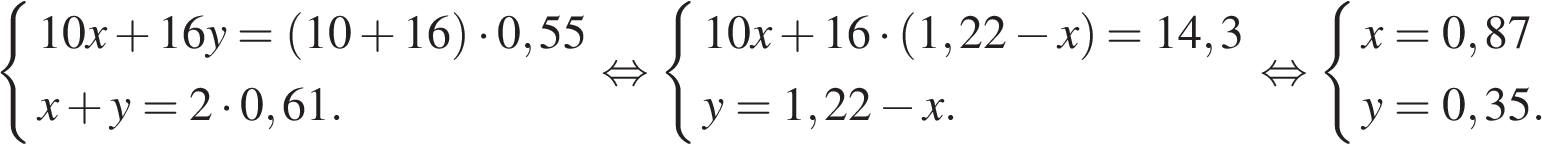
Таким об­ра­зом, в пер­вом рас­тво­ре со­дер­жит­ся 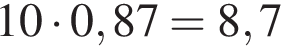  ки­ло­грам­ма кис­ло­ты.

Ответ: 8,7.

Ответ: 8,7

10. Име­ют­ся два со­су­да, со­дер­жа­щие 4 кг и 16 кг рас­тво­ра кис­ло­ты раз­лич­ной кон­цен­тра­ции. Если их слить вме­сте, то по­лу­чит­ся рас­твор, со­дер­жа­щий 57% кис­ло­ты. Если же слить рав­ные массы этих рас­тво­ров, то по­лу­чен­ный рас­твор будет со­дер­жать 60% кис­ло­ты. Сколь­ко ки­ло­грам­мов кис­ло­ты со­дер­жит­ся в пер­вом рас­тво­ре?

Ре­ше­ние.

Пусть кон­цен­тра­ция пер­во­го рас­тво­ра - х, кон­цен­тра­ция вто­ро­го рас­тво­ра - y. Со­ста­вим си­сте­му урав­не­ний со­глас­но усло­вию за­да­чи:

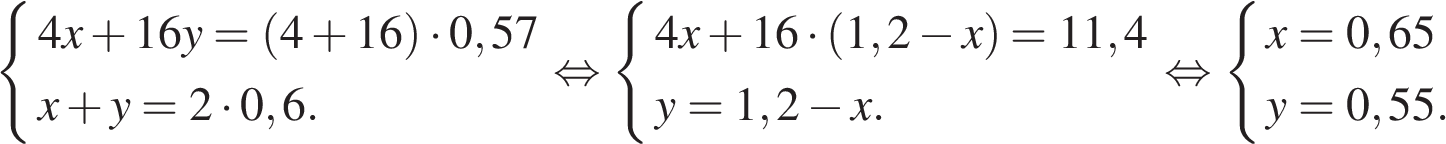
Таким об­ра­зом, в пер­вом рас­тво­ре со­дер­жит­ся 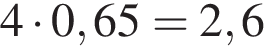  ки­ло­грам­ма кис­ло­ты

Ответ: 2,6

Ответ: 2,6

11. Име­ют­ся два со­су­да, со­дер­жа­щие 40 кг и 30 кг рас­тво­ра кис­ло­ты раз­лич­ной кон­цен­тра­ции. Если их слить вме­сте, то по­лу­чим рас­твор, со­дер­жа­щий 73% кис­ло­ты. Если же слить рав­ные массы этих рас­тво­ров, то по­лу­чен­ный рас­твор будет со­дер­жать 72% кис­ло­ты. Сколь­ко ки­ло­грам­мов кис­ло­ты со­дер­жит­ся во вто­ром рас­тво­ре?

Ре­ше­ние.

Пусть кон­цен­тра­ция пер­во­го рас­тво­ра - х, кон­цен­тра­ция вто­ро­го рас­тво­ра - y. Со­ста­вим си­сте­му урав­не­ний со­глас­но усло­вию за­да­чи:

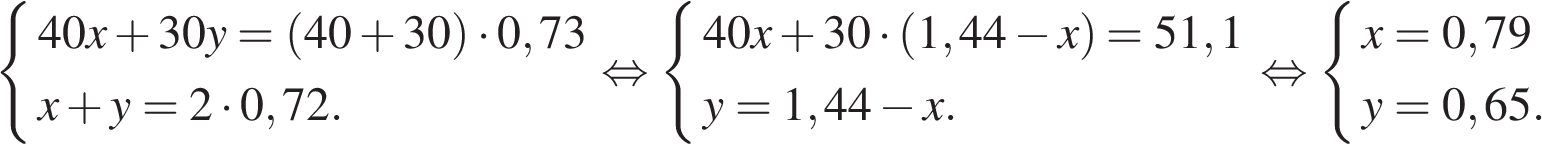
Таким об­ра­зом, во вто­ром рас­тво­ре со­дер­жит­ся   ки­ло­грам­ма кис­ло­ты

Ответ: 19,5

Ответ: 19,5

12. Име­ют­ся два со­су­да, со­дер­жа­щие 40 кг и 20 кг рас­тво­ра кис­ло­ты раз­лич­ной кон­цен­тра­ции. Если их слить вме­сте, то по­лу­чит­ся рас­твор, со­дер­жа­щий 33% кис­ло­ты. Если же слить рав­ные массы этих рас­тво­ров, то по­лу­чен­ный рас­твор будет со­дер­жать 47% кис­ло­ты. Сколь­ко ки­ло­грам­мов кис­ло­ты со­дер­жит­ся в пер­вом рас­тво­ре?

Ре­ше­ние.

Пусть кон­цен­тра­ция пер­во­го рас­тво­ра — х, кон­цен­тра­ция вто­ро­го рас­тво­ра — y. Со­ста­вим си­сте­му урав­не­ний со­глас­но усло­вию за­да­чи:

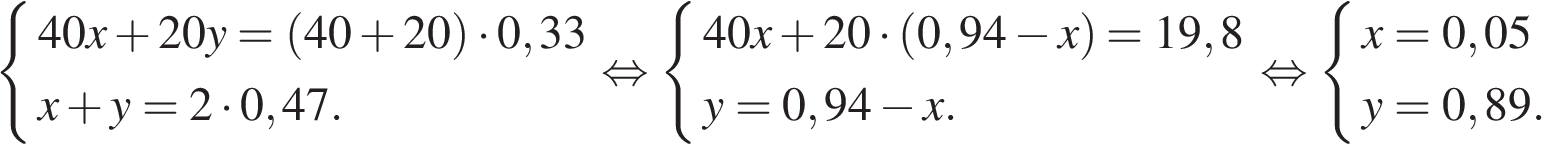
Таким об­ра­зом, во пер­вом рас­тво­ре со­дер­жит­ся 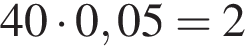  ки­ло­грам­ма кис­ло­ты.

Ответ: 2.

Ответ: 2

13. Име­ют­ся два со­су­да, со­дер­жа­щие 24 кг и 26 кг рас­тво­ра кис­ло­ты раз­лич­ной кон­цен­тра­ции. Если их слить вме­сте, то по­лу­чит­ся рас­твор, со­дер­жа­щий 39% кис­ло­ты. Если же слить рав­ные массы этих рас­тво­ров, то по­лу­чен­ный рас­твор будет со­дер­жать 40% кис­ло­ты. Сколь­ко ки­ло­грам­мов кис­ло­ты со­дер­жит­ся в пер­вом рас­тво­ре?

Ре­ше­ние.

Пусть кон­цен­тра­ция пер­во­го рас­тво­ра - х, кон­цен­тра­ция вто­ро­го рас­тво­ра - y. Со­ста­вим си­сте­му урав­не­ний со­глас­но усло­вию за­да­чи:

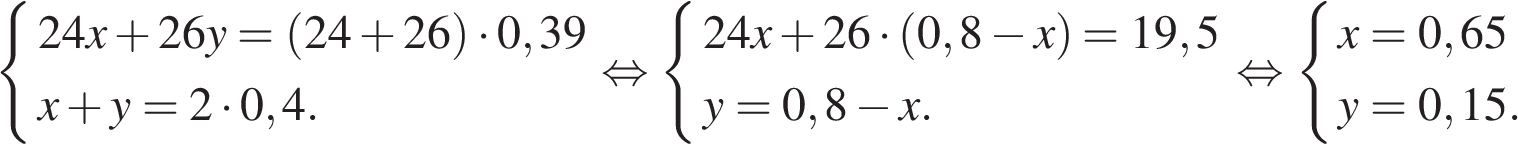
Таким об­ра­зом, во вто­ром рас­тво­ре со­дер­жит­ся 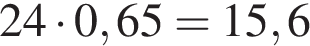  ки­ло­грам­ма кис­ло­ты

Ответ: 15,6

Ответ: 15,6

14. Име­ют­ся два со­су­да, со­дер­жа­щие 30 кг и 20 кг рас­тво­ра кис­ло­ты раз­лич­ной кон­цен­тра­ции. Если их слить вме­сте, то по­лу­чим рас­твор, со­дер­жа­щий 81% кис­ло­ты. Если же слить рав­ные массы этих рас­тво­ров, то по­лу­чен­ный рас­твор будет со­дер­жать 83% кис­ло­ты. Сколь­ко ки­ло­грам­мов кис­ло­ты со­дер­жит­ся во вто­ром рас­тво­ре?

Ре­ше­ние.

Пусть кон­цен­тра­ция пер­во­го рас­тво­ра - х, кон­цен­тра­ция вто­ро­го рас­тво­ра - y. Со­ста­вим си­сте­му урав­не­ний со­глас­но усло­вию за­да­чи:

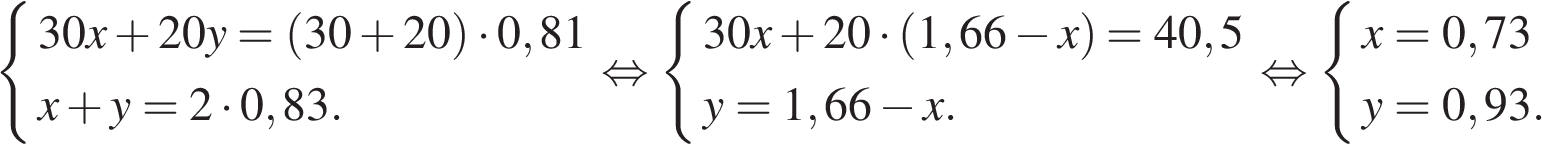
Таким об­ра­зом, во вто­ром рас­тво­ре со­дер­жит­ся 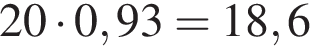  ки­ло­грам­ма кис­ло­ты

Ответ: 18,6

Ответ: 18,6

15. Име­ют­ся два со­су­да, со­дер­жа­щие 22 кг и 18 кг рас­тво­ра кис­ло­ты раз­лич­ной кон­цен­тра­ции. Если их слить вме­сте, то по­лу­чит­ся рас­твор, со­дер­жа­щий 32% кис­ло­ты. Если же слить рав­ные массы этих рас­тво­ров, то по­лу­чен­ный рас­твор будет со­дер­жать 30% кис­ло­ты. Сколь­ко ки­ло­грам­мов кис­ло­ты со­дер­жит­ся в пер­вом рас­тво­ре?

Ре­ше­ние.

Пусть кон­цен­тра­ция пер­во­го рас­тво­ра - х, кон­цен­тра­ция вто­ро­го рас­тво­ра - y. Со­ста­вим си­сте­му урав­не­ний со­глас­но усло­вию за­да­чи:

Таким об­ра­зом, в пер­вом рас­тво­ре со­дер­жит­ся 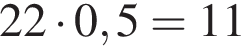  ки­ло­гра­мов кис­ло­ты

Ответ: 11

Ответ: 11

16. Име­ют­ся два со­су­да, со­дер­жа­щие 30 кг и 42 кг рас­тво­ра кис­ло­ты раз­лич­ной кон­цен­тра­ции. Если их слить вме­сте, то по­лу­чим рас­твор, со­дер­жа­щий 40% кис­ло­ты. Если же слить рав­ные массы этих рас­тво­ров, то по­лу­чен­ный рас­твор будет со­дер­жать 37% кис­ло­ты. Сколь­ко ки­ло­грам­мов кис­ло­ты со­дер­жит­ся во вто­ром рас­тво­ре?

Ре­ше­ние.

Пусть кон­цен­тра­ция пер­во­го рас­тво­ра - х, кон­цен­тра­ция вто­ро­го рас­тво­ра - y. Со­ста­вим си­сте­му урав­не­ний со­глас­но усло­вию за­да­чи:

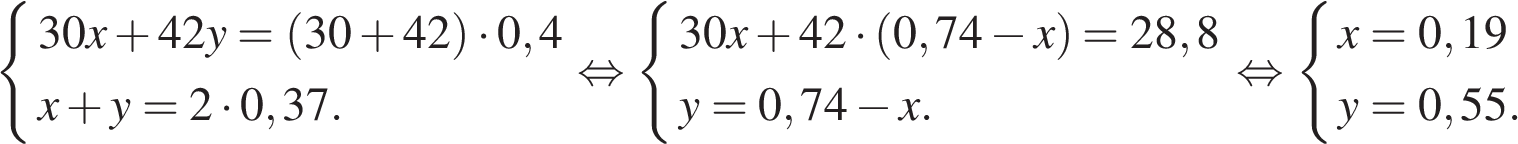
Таким об­ра­зом, во вто­ром рас­тво­ре со­дер­жит­ся 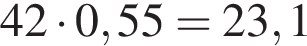  ки­ло­грам­мов кис­ло­ты

Ответ: 23,1

Ответ: 23,1

17. Име­ют­ся два со­су­да, со­дер­жа­щие 48 кг и 42 кг рас­тво­ра кис­ло­ты раз­лич­ной кон­цен­тра­ции. Если их слить вме­сте, то по­лу­чим рас­твор, со­дер­жа­щий 42% кис­ло­ты. Если же слить рав­ные массы этих рас­тво­ров, то по­лу­чен­ный рас­твор будет со­дер­жать 40% кис­ло­ты. Сколь­ко ки­ло­грам­мов кис­ло­ты со­дер­жит­ся во вто­ром рас­тво­ре?

Ре­ше­ние.

Пусть кон­цен­тра­ция пер­во­го рас­тво­ра - х, кон­цен­тра­ция вто­ро­го рас­тво­ра - y. Со­ста­вим си­сте­му урав­не­ний со­глас­но усло­вию за­да­чи:

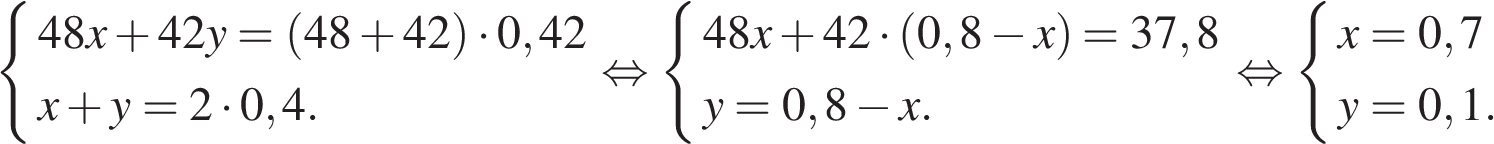
Таким об­ра­зом, во вто­ром рас­тво­ре со­дер­жит­ся 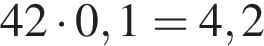  ки­ло­грам­ма кис­ло­ты

Ответ: 4,2

Ответ: 4,2

18. Све­жие фрук­ты со­дер­жат 88 % воды, а вы­су­шен­ные — 30 %. Сколь­ко тре­бу­ет­ся све­жих фрук­тов для при­го­тов­ле­ния 6 кг вы­су­шен­ных фрук­тов?

Ре­ше­ние.

За­ме­тим, что сухая часть све­жих фрук­тов со­став­ля­ет 12%, а вы­су­шен­ных — 70%. Зна­чит, для при­го­тов­ле­ния 6 кг вы­су­шен­ных фрук­тов тре­бу­ет­ся 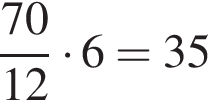  кг све­жих.

Ответ: 35 кг.

Ответ: 35

19. Сме­ша­ли не­ко­то­рое ко­ли­че­ство 21-про­цент­но­го рас­тво­ра­ не­ко­то­ро­го ве­ще­ства с таким же ко­ли­че­ством 95-про­цент­но­го рас­тво­ра ­это­го же ве­ще­ства. Сколь­ко про­цен­тов со­став­ля­ет кон­цен­тра­ция по­лу­чив­ше­го­ся рас­тво­ра?

Ре­ше­ние.

Пусть взяли 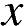  г 21-про­цент­но­го рас­тво­ра, тогда взяли и  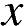 г 95-про­цент­но­го рас­тво­ра. Кон­цен­тра­ция рас­тво­ра — масса ве­ще­ства, раз­делённая на массу всего рас­тво­ра. В пер­вом рас­тво­ре со­дер­жит­ся  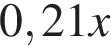 г, а во вто­ром —   г Кон­цен­тра­ция по­лу­чив­ше­го­ся рас­тво­ра равна 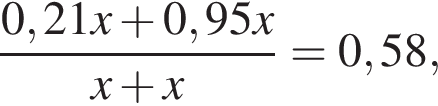  или 58%.

Ответ: 58.

Ответ: 58

20. Све­жие фрук­ты со­дер­жат 93% воды, а вы­су­шен­ные — 16%. Сколь­ко сухих фрук­тов по­лу­чит­ся из 252 кг све­жих фрук­тов?

Ре­ше­ние.

Све­жие фрук­ты со­дер­жат 7% пи­та­тель­но­го ве­ще­ства, а вы­су­шен­ные — 84%. В 252 кг све­жих фрук­тов со­дер­жит­ся 0,07 · 252 = 17,64 кг пи­та­тель­но­го ве­ще­ства. Такое ко­ли­че­ство пи­та­тель­но­го ве­ще­ства будет со­дер­жать­ся в 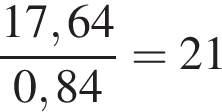  кг вы­су­шен­ных фрук­тов.

Ответ: 21.