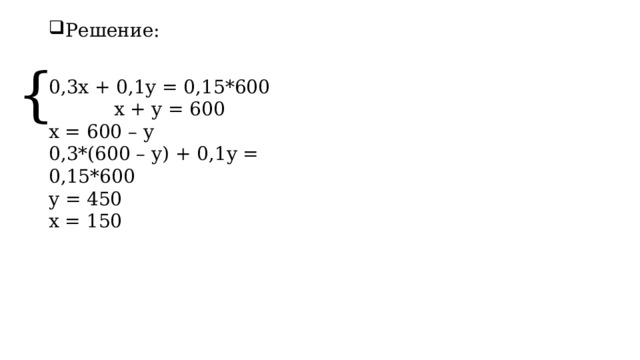Просмотр содержимого документа
«Задачи на проценты, сплавы, смеси»

Задачи на проценты, сплавы, смеси

Задача 1: Смешали 30% раствор соляной кислоты с 10% раствором и получили 600 гр 15% раствора. Сколько гр каждого раствора было взято?
- О чем говориться в задаче: о процессе смешивания 2-х растворов; о растворах: 30% раствор соляной кислоты, 10% раствор соляной кислоты, 600 гр 15% раствора соляной кислоты.
- Какой процесс: процесс смешивания двух растворов.
- Что именно говорится об этом процессе: об этом процессе говорится, что было взято два раствора соляной кислоты и смешав их, получили 3 раствор.

- Что известно об этом процессе?
- Первый раствор - 30% соляной кислоты;
- Второй раствор - 10% соляной кислоты;
- Получившийся третий раствор - 600 гр 15% соляной кислоты.
- Пусть x - масса первого раствора;
- Пусть y - масса второго раствора.

- Что требуется найти в задаче?
В задаче требуется найти массы первого и второго раствора, учитывая, что при их смешивании получилось 600 гр 15% раствора. То есть - найти x и y.

- Обозначения: x – масса первого раствора, y - масса второго раствора.
- Уравнения:
0,3x + 0,1y = 0,15*600 или 0,3x + 0,1y = 0,15*600
{
{
0,3x + 0,1y = 0,15*600
x + y = 600
0,3x + 0,1y = 0,15*600
x + y = 600
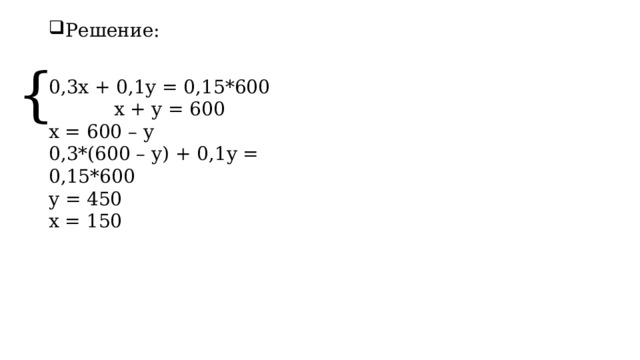
{
0,3x + 0,1y = 0,15*600
x + y = 600
x = 600 – y
0,3*(600 – y) + 0,1y = 0,15*600
y = 450
x = 150

- Ответ: чтобы получить 600 гр 15% раствора соляной кислоты, необходимо взять 450 гр 30% раствора соляногй кислоты и 150 гр 10% раствора соляной кислоты.

- План работы решения задачи:
- Определили состояния веществ и процессы, которые происходят с ними (3 состояния и 1 процесс);
- Записали, что именно говорится о них (первый 30% раствор соляной кислоты, второй 10% раствор соляной кислоты, получившийся третий 600 гр 15% раствор соляной кислоты);
- Составили уравнения для того, чтобы ответить на вопрос задачи (сколько гр каждого раствора было взято);
- Решили систему уравнений;
- Записали ответ.

Задача 2: От пристани A к пристани B, расстояние между которыми равно 110 км, отправился с постоянной скоростью первый теплоход, а через 1 час после этого следом за ним со скоростью на 1 км/ч большей отправился второй. Найдите скорость второго теплохода, если в пункт B он прибыл одновременно с первым.

- О чем говорится в задаче: о двух процессах; первый теплоход и второй теплоход.
- Какой процесс: процессы движения двух теплоходов.
- Что именно говорится об этих процесах: что первый теплоход вышел из пункта А в пункт В с постоянной скоростью, а второй теплоход вышел по тому же маршруту спустя 1 час после первого.

- 1 процесс: первый теплоход вышел из пункта А в пункт В,расстояние между которыми равно 110км, с постоянной скоростью.
Пусть x – 1 - скорость первого теплохода.
- 2 процесс: второй теплоход вышел по тому же маршруту спустя 1 час после первого теплохода. Скорость второго на 1 км/ч больше первого теплохода.
Пусть x - скорость второго теплохода.
x-1 110 110/(x – 1)
x 110 110/x

- Что требуется найти в задаче:
В здаче требуется найти скорость второго теплохода. То есть - x.

- Обозначения: x - скорость второго теплохода, x –1 - скорость первого теплохода.
- Уравнение: так как первый теплоход находился в пути больше второго теплохода на 1 час, уравнение может иметь следующий вид.
110/(x – 1) - 110/x = 1

110/(x – 1) - 110/x = 1
(110x – 110x + 110)/x(x – 1) = 1
110/x(x – 1) = 1
x - x –110 = 0
D = 1 + 440 = 441
x = (1 + 21)/2 = 11
x = (1 – 21)/2 = -10 – не удовлетворяет условию задачи
2
1
2

- Ответ: скорость второго теплохода равна 11 км/ч.

- План работы решения задачи:
- Выявили 2 процесса (процессы движения двух теплоходов);
- Записали, что именно говорится о них (1 процесс - первый теплоход вышел из пункта А в пункт В,расстояние между которыми равно 110км, с постоянной скоростью, 2 процесс -второй теплоход вышел по тому же маршруту спустя 1 час после первого теплохода. Скорость второго на 1 км/ч больше первого теплохода);
- Составили уравнение, для того чтобы ответить на вопрос задачи (чему равна скорость второго теплохода);
- Решили уравнение;
- Записали ответ.

Задача 3: На изготовление 475 деталей первый рабочий тратит на 6 часов меньше, чем второй рабочий на изготовление 550 таких же деталей. Известно, что первый рабочий за час делает на 3 детали больше, чем второй. Сколько деталей в час делает первый рабочий?

- О чем говориться в задаче: о двух процессах; первый рабочий изготавливает детали, второй рабочий изготавливает детали.
- Какой процесс: процесс изготовления деталей, то есть работы двух рабочих.
- Что именно говорится об этих процессах: что первый рабочий изготавливает свои детали, затрачивая на это меньше часов, чем второй рабочий на изготовление своих деталей.

- 1 процесс: первый рабочий изготавливал - 475 деталей; за час делает на 3 детали больше чем второй рабочий.
Пусть x - количество деталей, которые делает первый рабочий за час.
- 2 процесс: второй рабочий изготавливает - 550 деталей.
Тогда, x-3 - количество деталей, которые делает второй рабочий за час.
x 475 475/x
x-3 550 550/(x-3)

- Что требуется найти в задаче?
В задаче требуется найти количество деталей, которые делает первый рабочий за час. То есть найти - x.

- Обозначения: x - количество деталей, которые делает первый рабочий за час.
- Уравнение: так как на изготовление 475 деталей первый рабочий тратит на 6 часов меньше, чем второй рабочий на изготовление 550 деталей, уравнение можно составить следующим образом.
475/x + 6 = 550/(x - 3)

475/x + 6 = 550/(x - 3)
(475 + 6x)/x = 550/(x – 3)
475x – 1425 + 6x - 18x = 550x
6x -93x – 1425 = 0
2x -31x – 475 = 0
D = 961 + 3800 = 4761
x = (31 + 69)/4 = 25
x = (31-69)/4 = -9,5 – не удовлетворяет условию задачи
2
2
2
1
2

- Ответ: первый рабочий делает 25 деталей в час.

- План работы решения задачи:
- Выявили 2 процесса (изготовление деталей);
- Записали, что именно говорится о них (1 процесс - первый рабочий изготавливает 475 деталей, 2 процесс - второй рабочий изготавливает 550 деталей; также известно, что первый рабочий за час делает на 3 детали больше, чем второй);
- Составили уравнение, для того чтобы ответить на вопрос задачи (сколько деталей в час делает первый рабочий);
- Решили уравнение;
- Записали ответ.