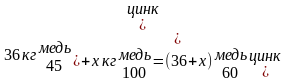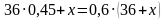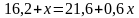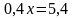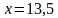Муниципальное общеобразовательное автономное учреждение средняя общеобразовательная школа №9 городского округа город Нефтекамск Республики Башкортостан
Исследовательская работа: Решение задач на смеси и сплавы
Выполнила: Яруллина Алина ученица 6б класса МОАУ СОШ №9
Руководитель Курбанова Зульфира Васимовна учитель математики
г. Нефтекамск
2021
ОГЛАВЛЕНИЕ
ВВЕДЕНИЕ 3
1. ТЕОРЕТИЧЕСКАЯ ЧАСТЬ 6
1.1 Из истории процентов 6
1.2 Основные типы задач на проценты 8
2. РЕШЕНИЕ ЗАДАЧ 9
2.1 Задачи на сплавы 9
2.2 Задачи на смеси 14
2.3 Задачи на «принцип сухого вещества» 19
ЗАКЛЮЧЕНИЕ 22
СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ 23
ВВЕДЕНИЕ
В любом открытии есть 99 % труда и потения
И только 1% таланта и способностей.
Л. Магницкий
Проценты – одно из математических понятий, которые часто встречаются в повседневной жизни. Так, часто мы слышим по телевидению, что, например, в выборах приняли участие 52,5% избирателей, рейтинг победителя хит-парада равен 75%, промышленное производство сократилось на 11,3%, уровень инфляции составляет 8% в год, банк начисляет 12% годовых и т.д.
Часто встречаются проценты и в периодической печати, в школьных учебниках и в другой информации.
Я перелистала учебники и заметили, что в каждом учебнике встречаются проценты, но чаще всего информацию в процентах можно увидеть в учебнике географии, истории, биологии, математики. Например, в учебнике географии читаю «Леса Башкортостана занимают более 40 % территории республики», а в учебнике истории – «Из центра рассылались указания: «Там, где проводится коллективизация, 3-5 процентов крестьян должны быть объявлены кулаками».
Все газеты и журналы публикуют рекламу, которая тоже не обходится без процентов.
Объявление в газете
«Слуховые аппараты стоят 1500 руб.
Скидка 10% только пенсионерам».
Проценты можно увидеть также и на этикетках, например,
«Кефир Жирность 1%». (Приложение 1)
Взрослые пользуются процентами при оформлении кредитов или при вкладах сбережений в банк.
Мои 3 брата и одна сестра сдавали ЕГЭ и объясняли старшие младшим, как решаются задачи на сплавы и растворы и от них же услышала о «методе сухого вещества» при решении задач. Для выяснения этих вопросов мы провели тестирование «Знакомы ли вы с процентами?»
Результаты тестирования
| Вопрос | Ученики (12 человек) | Взрослые (22 человека) |
| верно | неверно | верно | неверно |
| 1.Что такое процент? А. одна сотая величины Б. одна десятая величины В. не знаю | 42% | 58% | 100% | 0% |
| 2. Цена товара увеличилась на 20%. Сколько будет стоить товар, если его первоначальная цена была 150 рублей? А. 170р. Б.180р. В. не известно | 66% | 34% | 100% | 0% |
| 3. Цена товара уменьшилась в два раза. На сколько процентов произошло снижение цены? А. 50% Б. 5% В. не знаю | 50% | 50% | 100% | 0% |
| 4. Сравните 52% от 60 и 60% от 52 А. больше Б. меньше В. равно | 42% | 58% | 75% | 25% |
| 5. В городских новостях прозвучало сообщение: цена одного товара, пользовавшегося повышенным спросом, в течение года выросла с 18 до 28 р., т. е. почти на 30%. Верный ли вывод сделан о росте цены? А. да Б. нет | 66% | 34% | 77% | 23% |
| 6. На весенней распродаже в магазине товар стоимостью 350 рублей уценили на 40%, а через неделю ещё на 5%. В супермаркете такой же товар уценили на 5%, а через неделю ещё – на 40%. А на ярмарке этот же товар уценили на 45%. Где выгоднее купить товар? А. в магазине Б. в супермаркете В. на ярмарке | 58% | 42% | 77% | 23% |
| 7. Нужны ли вам знания о процентах? А. да Б. нет В. не знаю | 75% | 25% | 100% | 0% |
Рис.1.Ученики Рис 2. Взрослые
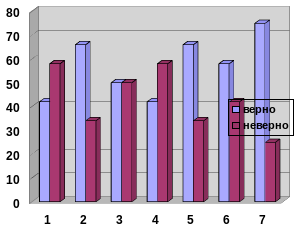
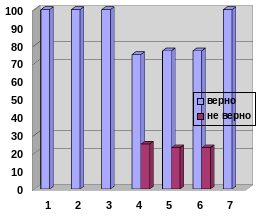
Анализируя данные тестирования, можно сделать вывод, что знания по теме «Процент» у взрослых лучше, чем у учеников.
На основании выше изложенного мы сделали выводы:
Оказывается, проценты встречаются:
-
на работе у взрослых, в школе, на рекламных щитах,
-
на экранах телевизора, в периодической печати;
-
Нельзя сегодня людям без знаний процентов!
Цель нашей работы:
Доказать, что тема «Проценты» актуальна во все времена
Задачи:
-
Изучить и проанализировать сведения из различных источников о процентах
-
Систематизировать полученные сведения
-
Изучить решение задач на смеси и сплавы
Объект исследования: процент.
Предмет исследования: использование данного объекта в жизни
Метод исследования: систематизация и обработка данных.
1. ТЕОРЕТИЧЕСКАЯ ЧАСТЬ 1.1 Из истории процентов
Задачи: изучить историю происхождения процентов, систематизировать знания о процентах.

Школьный этимологический словарь русского языка
ПРОЦЕНТ. Заимств. в Петровскую эпоху из нем. яз., где Procent
pro centum «за сто», см. про, сто, цент.
ПРО. Общеслав. Того же корня, что др.-прус. pra "через, для", греч.
pro "перед, до" и т. д.
СТО. Общеслав. индоевроп. характера. Общеслав. sъto родственно авест. satəm, лат. centum, тохар. känt и т. д.
ЦЕНТ. Заимств. во второй половине XIX в. из англ. яз., где cent "сотая доля доллара" centum "сто". См. сто.
ПРОЦЕНТ (от лат . pro centum - за сто), сотая доля числа; обозначается знаком %.
Слово «процент» происходит от латинских слов pro centum, что буквально означает «сто ста». Проценты дают возможность легко сравнивать между собой части целого, упрощают расчёты и поэтому очень распространены.
Широко начали использоваться проценты в Древнем Риме, но идея процентов возникла много раньше - вавилонские ростовщики уже умели находить проценты (но они считали не «со ста», а «с шестидесяти», так как в Вавилоне пользовались шестидесятеричными дробями).
В 1685 году в Париже была издана книга «Руководство по коммерческой арифметике» Матье де ла Порта. В одном месте речь шла о процентах, которые тогда обозначали «cto» (сокращенно от cento). Однако наборщик принял это «cto» за дробь и напечатал «%». Так из-за опечатки этот знак вошёл в обиход.
После этой ошибки многие математики также стали употреблять знак %
для обозначения процентов, и постепенно он получил всеобщее признание.
Были известны проценты и в Индии.
Индийские математики вычислили проценты, применяя так называемое тройное правило, то есть пользуясь пропорцией.
В Европе в средние века расширилась торговля и, следовательно, особое внимание обращалось на умение вычислять проценты. Тогда приходилось рассчитывать не только проценты, но и проценты с процентов (сложные проценты). Часто конторы и предприятия для облегчения расчетов разрабатывали особые таблицы вычисления процентов. Эти таблицы держались в тайне, составляли коммерческий секрет фирмы. Впервые таблицы были опубликованы в 1584 году Симоном Стевином.
Историческая справка

Нидерландский математик и инженер. Родился в Брюгге в 1548г. В молодости работал счетоводом. В 1571-1581гг. путешествовал по Европе. С 1581г. жил в Лейдене, Дельфте, Гааге. Преподавал в Лейденском университете, служил инженером в армии принца Оранского. Последние годы жизни работал инспектором водных сооружений. Умер в 1620 год.
1.2 Основные типы задач на проценты
Полезно знать: Чтобы выразить проценты десятичной дробью, нужно число, стоящее перед знаком %, разделить на 100.
65% -0,65 150% -1,5 0,13% - 0,0013
Основные типы задач
1 тип.
Чтобы найти, сколько процентов одно число составляет от другого, нужно первое число разделить на второе и полученную дробь записать в виде процентов.
Пример. Определить процент посещаемости школьников 25 декабря, если из 44 учеников школы присутствовали 34.
34/44=0,77 - 77%
2 тип
Чтобы найти указанное число процентов от данного числа, нужно данное число умножить на проценты, выраженные десятичной дробью.
Пример. Согласно российским законам заработок человека облагается подоходным налогом, который составляет 13% заработка. Какую сумму в качестве подоходного налога должен заплатить человек, заработавший 12740 рублей?
13% - 0,13
12740*0,13=1656,2р.
3 тип
Если дано, сколько процентов от искомого числа составляет данное число, то, чтобы найти искомое число, нужно заменить проценты десятичной дробью и разделить на эту дробь данное число.
Пример. Рабочему выдали 30% от заработной платы, что составило 4250 р. Сколько рублей составляет вся заработная плата?
30% - 0,3
4250/0,3=14166,67р
Замечание. Задачи можно решить и другими способами, но кажется, что данным способом эти задачи решать удобнее.
2. РЕШЕНИЕ ЗАДАЧ
2.1 Задачи на сплавы
Задача №1
Имеется два сплава меди и свинца. Один сплав содержит 15% меди, а другой – 65% меди. Сколько нужно взять каждого сплава, чтобы получилось 200г сплава, содержащего 30% меди?
-
Рассмотрим решение задач с применением таблицы. Таблица для решения задач имеет вид:
| Наименование веществ, растворов, смесей, сплавов | Процентное содержание меди (доля содержания вещества) | Масса раствора (смеси, сплава) | Масса вещества |
| Первый сплав | 15% = 0,15 | x, г | 0,15* x |
| Второй сплав | 65% = 0,65 | (200 – x) г | 0,65*(200 – x) =130 – 0,65 x |
| Получившийся сплав | 30% = 0,3 | 200 г | 200*0,3 = 60 |
Сумма масс меди в двух первых сплавах (то есть в первых двух строчках) равна массе меди в полученном сплаве (третья строка таблицы)
0,15 x + 120 – 0,65 x = 60.
Решив это уравнение, получаем x = 140. При этом значения x выражение 200 – x = 60. Это означает, что первого сплава надо взять 140г, а второго 60 г.
-
Рассмотрим решение этой же задачи с помощью следующей модели. Изобразим каждый из растворов в виде прямоугольника, разбитого на два фрагмента (по числу составляющих элементов). Для того чтобы показать, что происходить смешивание веществ, поставим знак «+» между первым и вторым прямоугольниками, а знак «=» между вторым и третьим прямоугольниками показывает, что третий раствор в результате смешивание первых двух. Полученная схема имеет вид:
медь медь медь

Решение:
Пусть x г – масса первого сплава. Тогда (200 – x)г – масса второго сплава. Дополнительным последнюю схему этими выражениями. Получим следующую схему:
медь медь медь

x г (200 – x)г 200 г.
Сумма масс меди в двух первых сплавах (то есть слева от знака равенства) равна массе меди в полученном третьем сплаве (справа от знака равенства):
0,15 x + 0,65 ∙ (200 – x) = 0,3 ∙ 200.
Решив это уравнение, получаем x = 140. При этом значении x выражение 200 – x =60. Это означает, что первого сплава надо взять 140 г, а второго – 60г.
Ответ: 140г, 60г.
-
Старинный способ решения задач на смеси, сплавы и растворы. Впервые о нем было упомянуто в первом печатном учебнике математики Леонтия Магницкого. Ввиду большой простоты предложенный способ применялся купцами и ремесленниками при решении различных практических задач. Но в задачниках и различных руководствах для мастеров и торговцах никаких обоснований и разъяснений не приводилось. Просто давался рецепт решения: либо, как в предыдущей задаче, рисовалась схема, либо словесно описывалась последовательность действий – поступай так и получишь ответ.
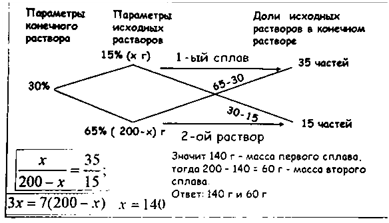
Изображаем каждую смесь (сплав) в виде прямоугольника, разбитого на фрагменты, количество которых соответствует количеству составляющих эту смесь (этот сплав) элементов.
Задача №2. Сплавили 2 кг цинка и меди, содержащего 20% цинка, и 6 кг сплава цинка и меди, содержащего 40% цинка. Найдите процентную концентрацию меди в получившемся сплаве.
Изобразим каждый сплав в виде прямоугольника, разбитого на два фрагмента (по числу составляющих элементов). На модели отобразим характер операции: сплавление – знак «+», после двух прямоугольников поставим знак «=», показывая, что третий сплав получен в результате сплавления первых двух.
Заполняем получившиеся прямоугольники в соответствие с условием задачи:
1) Указываем компоненты сплава, сохраняя порядок соответствующих букв.
2) Вписываем процентное содержание соответствующего компонента. Процентное содержание второго компонента равно разности 100% и процентного содержания первого.
3) Перед прямоугольником записываем массу (или объём) соответствующего сплава (или компонента).
Представим этот процесс в виде следующей схемы:
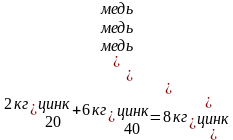
Решение.
Пусть процентная концентрация меди в получившемся сплаве х. Найдём процентное содержание второго компонента. Дополним схему этими выражениями:
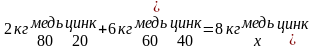
Так как по меди известны все компоненты, то составим уравнение:
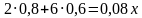
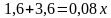
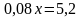
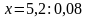
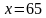
Ответ: 65%.
Задача №4. Сплавляется лом двух сортов с содержанием никеля 5% и 40%. Сколько нужно взять металла второго из этих сортов, чтобы получить 140т стали с содержанием 30% никеля?
x т – металла второго сорт, (140 – x) т – металла первого сорта.
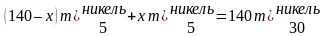
Составим уравнение: 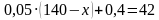
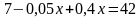
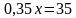
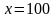
Ответ: 100
Задача №4. Кусок сплава меди и цинка массой в 36 кг содержит 45% меди. Какую массу меди нужно добавить к этому куску, чтобы полученный новый сплав содержал 60% меди?
Решение.
х кг – меди нужно добавить, а 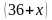 кг масса нового сплава.
кг масса нового сплава.
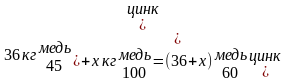
Составим уравнение: 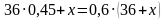
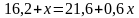
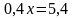
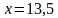
Ответ: 13,5 кг.
Задача №5 В 1 кг сплава меди и олова содержится 45% олова. Сколько граммов меди надо добавить к этому сплаву, чтобы процентное содержание олова в новом сплаве стало равным 15%?
Решение.
х г – меди надо добавить, а  масса нового сплава.
масса нового сплава.
Составим уравнение по меди:



Ответ: 2000 г.
Задача №6. Бронза является сплавом меди и олова (в разных пропорциях). Кусок бронзы, содержащий 1/12 часть олова, сплавляется с другим куском, содержащим 1/10 часть олова. Полученный сплав содержит 1/11 часть олова. Найдите вес второго куска, если вес первого равен 84 кг.
Решение.
х кг – вес второго куска.
Составим уравнение:  х=
х=




Ответ: 70 кг.
Задача №7. У ювелира два одинаковых по массе слитка, в одном из которых 36% золота, а в другом 64%. Сколько процентов золота содержится в сплаве, полученном из этих слитков?
Решение.
х – масса слитка, а у% – золота в полученном сплаве.
Составим уравнение:


Ответ: 50%.
Задача №8. К некоторому количеству сплава меди с цинком, в котором эти металлы находятся в отношении 2:3, добавили 4 кг чистой меди. В результате получили новый сплав, в котором медь и цинк относятся как 2:1. Сколько килограмм нового сплава получилось?
Решение.
Прежде чем составлять схему, уточним, что в первом сплаве медь составляет  , а в полученном новом сплаве -
, а в полученном новом сплаве -  . Обозначим массу полученного сплава х кг, и, внеся указанные части в соответствующие фрагменты схемы, получаем:
. Обозначим массу полученного сплава х кг, и, внеся указанные части в соответствующие фрагменты схемы, получаем:
Нетрудно составить уравнение, подсчитав количество меди слева от знака неравенства, и приравняв его к количеству меди, справа от него. Получаем уравнение: Решив его, получаем искомое значение: х=9.
Замечание. Можно было составить уравнение на основе подсчета массы цинка в обеих частях неравенства. Для этого внесем в схему необходимые данные:
1)если в первом сплаве медь составляет часть  , то цинк –
, то цинк –  ;
;
2) если в полученном сплаве медь составляет часть  , то цинк –
, то цинк –  .
.
Уравнение в этом случае имеет вид:  Это уравнение равносильно предыдущему.
Это уравнение равносильно предыдущему.
Ответ: х=9кг.
2.2 Задачи на смеси
Задача №1 У хозяйки было 100г 70%-ого уксуса. Сколько граммов воды нужно добавить, что бы получить уксус 10%-ой концентрации?
-
Рассмотрим решение задач с применением таблицы. Таблица для решения задач имеет вид:
| Наименование веществ, растворов, смесей, сплавов | Процентное содержание меди (доля содержания вещества) | Масса раствора (смеси, сплава) | Масса вещества |
| Раствор 70%-го уксуса | 70% = 0,7 | 100 г | 0,7* x |
| Вода | 0% = 0 | x, г | 0 |
| Получившийся раствор | 10% = 0,1 | (x + 100) г | 0,1*(x + 100) |
Количество уксуса в старом и новом растворах не изменяется, учитывая это, составляем уравнение:
медь медь медь

Решение:
Пусть x г – масса первого сплава. Тогда (200 – x)г – масса второго сплава. Дополнительным последнюю схему этими выражениями. Получим следующую схему:
вода уксус вода вода уксус

x мл (1000 – x)мл 1000 мл.
01 * (x + 100) = 0,7 * 100
x = 600 г
Ответ: 600 г
Рассмотрим решение это задачи с помощью пропорции
масса процентная концентрация


Зависимость между массой и процентной концентрацией обратно пропорциональная, так как если уменьшить концентрацию уксуса в несколько раз, то масса во столько же раз увеличится. Условно обозначим такую зависимость противоположно направленными стрелками. Запишем пропорцию:
 ;
;  ;
;  ;
;  .
.
Ответ: 600 г.
Задача №2. У хозяйки было некоторое количество 70%-ной уксусной кислоты. После того, как она добавила в кислоту 3200 г воды, у неё получился 6%-ный уксус. Сколько граммов 70%-ной уксусной кислоты было первоначально у хозяйки?
Решение.
Пусть х граммов 70%-ной уксусной кислоты было первоначально, а
 г–масса полученного 6%-ного уксуса. Условие задачи имеет следующий вид:
г–масса полученного 6%-ного уксуса. Условие задачи имеет следующий вид:
масса процентная концентрация

Запишем пропорцию:
;  ;
; 

Ответ: 300 граммов.
Задача №3. В лаборатории изготовили 1 кг 16% солевого раствора. Через неделю из этого раствора испарилось 200 г воды. Определите процентное содержание соли в новом растворе.
Решение.
Пусть х процентное содержание соли в новом растворе.

Узнаем массу нового раствора после испарения воды:  .
.
Условие задачи имеет следующий вид:
масса процентная концентрация
↓
Запишем пропорцию:
 ;
;  ;
;  ;
; 
Ответ: 20% соли в новом растворе.
Задача №4. Для консервирования 10 кг баклажан необходимо 0,5 л столового уксуса (10% раствор уксусной кислоты). У хозяйки имеется уксусная эссенция (80% раствор уксусной кислоты). Сколько миллилитров уксусной эссенции понадобится хозяйке для консервирования 20 кг баклажан?
Решение.
Для консервирования 20кг баклажан понадобится 1л или 1000мл столового уксуса (10% раствор уксусной кислоты).
Условие задачи имеет следующий вид:
объём процентная концентрация
Запишем пропорцию:
 ;
;  ;
;  ;
; 
Ответ: 125 миллилитров.
Задача №5. Имеется 10 литров 60%-ного раствора соли. Сколько литров воды нужно долить, чтобы получить 40%-ный раствор соли?
Решение.

 ;
;  ;
;  ;
; 

Ответ: 5 литров.
Задача №6. Имеется 1 грамм 69%-ной уксусной кислоты. Сколько граммов воды нужно долить, чтобы получить 3%-ный раствор уксуса?
Решение.

 ;
;  ;
;  ;
; 
Ответ: 22 грамма.
Задача №7. У хозяйки есть 5 кг сахарного сиропа 50% концентрации. Сколько литров кипячёной воды необходимо добавить для получения сиропа 40% концентрации?
Решение.


 ;
;  ;
;  ;
; 

Ответ: 1,25 литров.
Задача №8. Кислый маринад для консервирования овощей содержит 24% столового уксуса (10% раствор уксусной кислоты). У хозяйки имеется уксусная эссенция (80% раствор уксусной кислоты). Сколько процентов уксусной эссенции должно содержаться в аналогичном маринаде?
Решение.
 ;
;  ;
;  ;
; 
Ответ: 3% уксусной эссенции.
Задача №9. По рецепту засолки огурцов на каждые 10 л рассола необходимо добавить 1 л столового уксуса (10% раствор уксусной кислоты). У хозяйки имеется уксусная эссенция (80% раствор уксусной кислоты). Сколько миллилитров уксусной эссенции понадобится хозяйке для приготовления 5 л рассола?
Решение.

↓
 ;
;  ;
;  ;
; 
125 мл для 10 л рассола, то для 5 л рассола 
Ответ: 62,5 миллилитров.
Задача №10. Морская вода содержит 4% (по массе) соли. Сколько килограммов чистой воды надо выпарить из 30 кг морской воды, чтобы содержание соли в последней составляло 12%?
Решение.
х кг чистой воды нужно выпарить.
↓
 ;
;  ;
;  ;
; 
Ответ: 20 кг чистой воды нужно выпарить.
Задача №11. Морская вода содержит 5% (по массе) соли. Сколько килограммов пресной воды надо прибавить к 40 кг морской воды, чтобы содержание соли в последней составляло 2%?
Решение.
х кг пресной воды нужно прибавить.
↓
 ; ;
; ;  ;
; 
Ответ: 60 кг пресной воды.
2.3 Задачи на «принцип сухого вещества»
1. Свежие абрикосы содержат 80% воды по массе, а курага (сухие абрикосы)- 12% воды. Сколько понадобится килограммов свежих абрикосов, чтобы получить 10 кг кураги?
Решение.
Будем рассматривать абрикосы как смесь некого «сухого вещества» и воды. При хранении и усушке масса «сухого вещества» не изменяется, поэтому найдём его процентную концентрацию в свежих абрикосах и в кураге:
 сухого вещества в свежих абрикосах.
сухого вещества в свежих абрикосах.
Составим таблицу: масса процентная концентрация сухого вещества
↓
Запишем пропорцию:
 ;
;  ;
;  ;
; 
Ответ: 44 кг свежих абрикосов.
2. Абрикосы при сушке теряют 60% своей массы. Сколько процентов воды содержат свежие абрикосы, если в сушёных абрикосах 25% воды?
Решение.
Узнаем концентрацию абрикос после сушки: 
 х кг масса свежих абрикос, то кураги 0,4х кг.
х кг масса свежих абрикос, то кураги 0,4х кг.
Находим процентную концентрацию «сухого вещества»:
В свежих абрикосах «сухое вещество» возьмём за , а в кураге вычислим
, а в кураге вычислим

Составим таблицу: масса процентная концентрация сухого вещества
↓
Запишем пропорцию и найдём  :
:
 ;
;
30% сухого вещества в свежих абрикосах, тогда воды 100-30=70%
Ответ: 70% воды содержат свежие абрикосы.
3. В свежих яблоках 80% воды, а в сушёных – 20%. На сколько процентов уменьшается масса яблок при сушке?
Решение.
Находим «сухое вещество» в свежих и сушёных яблоках:
 «сухого вещества» в свежих яблоках.
«сухого вещества» в свежих яблоках.
 «сухого вещества» в сушёных.
«сухого вещества» в сушёных.
Пусть .
Составим таблицу:
↓
Запишем пропорцию и найдём  :
:
 ;
;  ;
; 
Так как масса свежих яблок была  , а сушёных стала узнаем, на сколько же килограммов уменьшилась масса при сушке:
, а сушёных стала узнаем, на сколько же килограммов уменьшилась масса при сушке:
 , а
, а 
Ответ: на 75%.
4. Свежесрезанные грибы содержат 90% воды. После длительного хранения 120 кг грибов на складе содержание воды в них уменьшилось до 84%. Какой стала масса грибов после хранения?
Решение.
.
↓
 ;
;  ;
; 
Ответ: 75 кг стала масса после хранения.
5. Свежая клюква состоит на 99% из воды. Заготовители собрали 500 кг клюквы и сдали её на склад. После длительного хранения на складе содержание воды в клюкве уменьшилось до 96%. Сколько килограммов весит клюква после хранения?
Решение.
 сухого вещества в клюкве.
сухого вещества в клюкве.
 сухого вещества стало в клюкве после длительного хранения.
сухого вещества стало в клюкве после длительного хранения.
↓
 ;
; 
Ответ: 125 кг.
6. Зёрна свежей кукурузы содержат 40% влаги, а кукурузные хлопья – 8% влаги. Сколько килограммов свежей кукурузы нужно переработать, чтобы получить 15 кг кукурузных хлопьев?
Решение.
 сухого вещества в свежей кукурузе.
сухого вещества в свежей кукурузе.
 сухого вещества в кукурузных хлопьях.
сухого вещества в кукурузных хлопьях.
↓
 ;
;
Ответ: 23 кг.
7. Свежие грибы по весу содержат 90% воды, а сухие 12% воды. Сколько получится сухих грибов из 22 кг свежих?
Ответ:2,5 кг.
ЗАКЛЮЧЕНИЕ
Если вы хотите участвовать в большой жизни, то наполняйте свою голову математикой, пока есть к тому возможность. Она окажет вам потом огромную помощь во всей вашей работе.
М.И Калинин
Работа закончена. Проведенная работа нам была интересна. Выявили, что проценты глубоко проникли во все сферы нашей жизни:
-
пищевую промышленность,
-
фармакологию,
-
нефтяную промышленность,
-
ювелирной,
-
строительной,
-
химической и.т.д.
Познавая много нового и интересного, мы поняли, чтобы разбираться в более сложных ситуациях, связанных с процентами, нужны знания из экономики. Подводя итог работы, приходим к выводу, что данная тема – актуальна. Как появились проценты, как изменялись, что несли народам и как влияли на их жизнь? Это интересно и актуально сегодня.
В своем исследовании мы думаем, что доказали, что тема « Проценты» актуальна во все времена и особенно в настоящее время. Думаем, что неправы наши сверстники, которые считают, что им не нужны знания о процентах. Без элементарных знаний по этой теме не сможешь ориентироваться в современной жизни.
СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ
1. Е.А.Семенко и др.Обобщающее повторение курса алгебры и начал анализа. Краснодар: «Просвещение-Юг», 2005.Ч.1. – 156с
2. Е.А.Семенко и др.Тестовые задания для подготовки к ЕГЭ – 2008 по математике.. Краснодар: «Просвещение-Юг», 2008.Ч.2. – 103с
3. Е.А.Семенко и др.Тестовые задания для подготовки к ЕГЭ – 2008 по математике.. Краснодар: «Просвещение-Юг», 2006.Ч 3. – 121с
4. Хоркина Н.А, Как помочь ученикам решать логарифмические уравнения и неравенства. МПГУ
5. Д,Гущин Сборник заданий по алгебре для подготовки к ЕГЭ и конкурсным экзаменам. Пособие для учителей./Париж, СПб: Стетоскоп, ВВМ, 2008. – 114с
6.Высоцкий И.Р., Гущин Д.Д. Интенсивный курс подготовки к ЕГЭ.М.: Айрис – пресс,2004.-304с.
7.Высоцкий И.Р., Гущин Д.Д. и др. ЕГЭ 2010. Математика. Универсальные материалы для подготовки учащихся /ФИПИ – М.: Интеллект-Центр, 2010. – 96с.
8. Математика в школе №№ 4,5 1998г.
9. 2. И.Ф. Шарыгин. Факультативный курс по математике. Решение задач. Учебное пособие для 10 класса средней школы. Москва «Просвещение» 1989.
10. Ткачук Лариса Андреевна, учитель математики МОУ лицея №4 г.Ейска Краснодарского края, Интернет ресурсы.
учитель математики МОУ лицея №4 г.Ейска Краснодарского края, Интернет ресурсы.












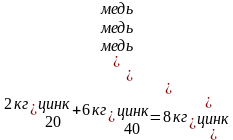
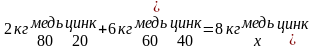
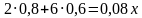
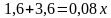
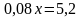
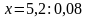
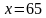
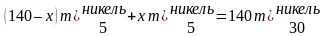
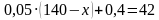
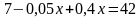
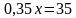
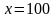
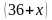 кг масса нового сплава.
кг масса нового сплава.