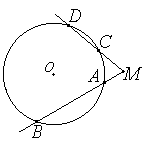| 1. Найдите больший угол равнобедренной трапеции ABCD, если диагональ АС образует с основанием AD и боковой стороной АВ углы, равные 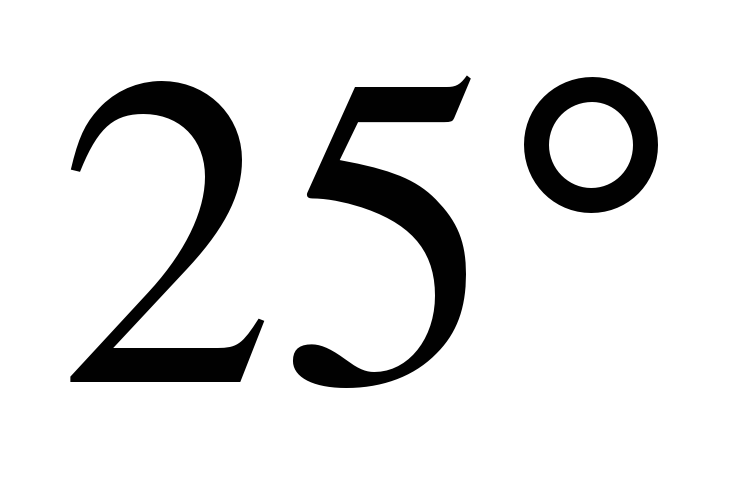 и и  соответственно. соответственно. | 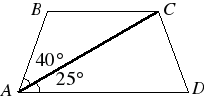
|
| 2. Найдите угол 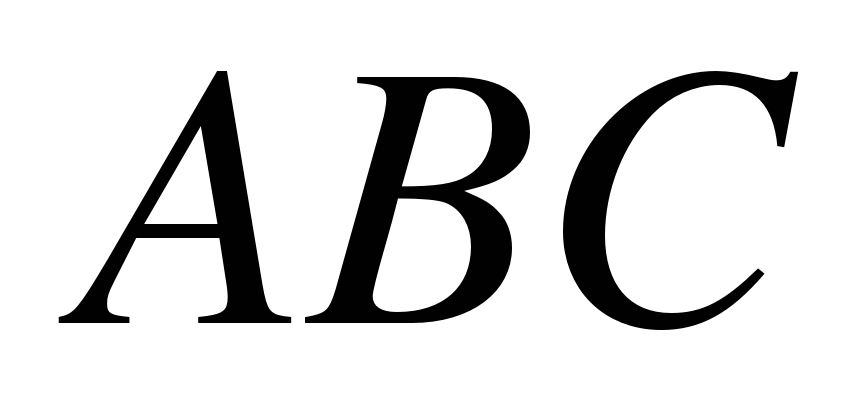 равнобедренной трапеции равнобедренной трапеции 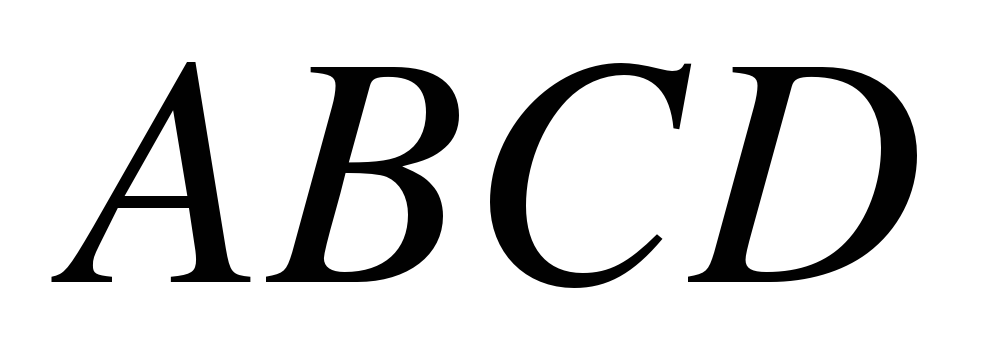 , если диагональ , если диагональ 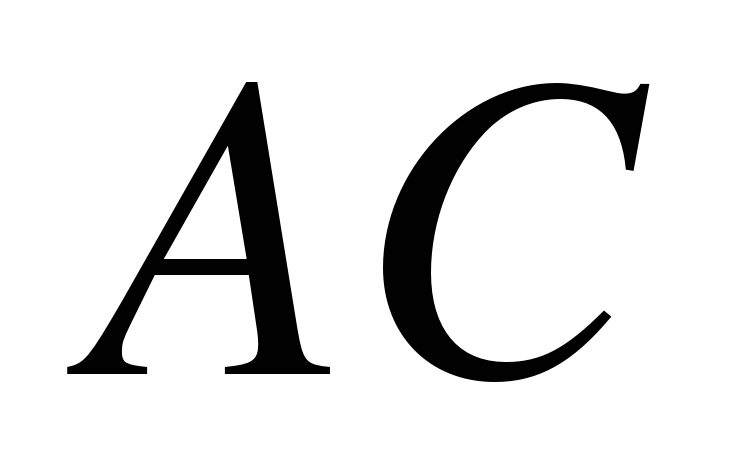 образует с основанием образует с основанием  и боковой стороной и боковой стороной 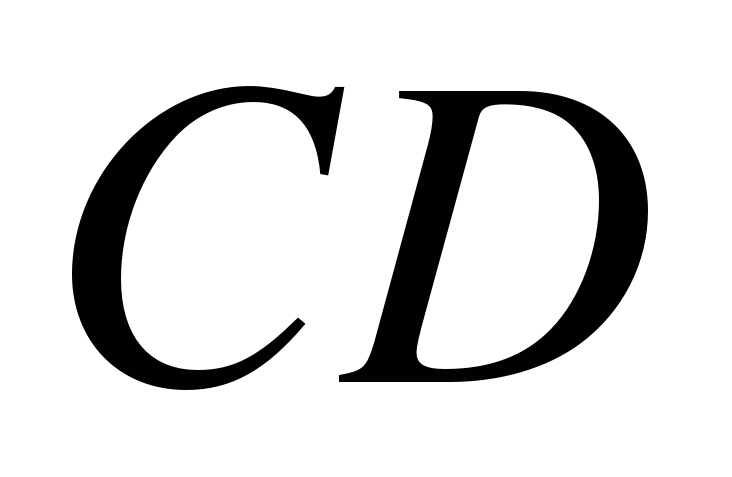 углы, равные углы, равные  и и  соответственно. соответственно. | 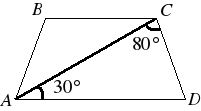
|
| 3. В трапеции средняя линия равна 12, меньшее основание 5. Найдите длину большего основания. |
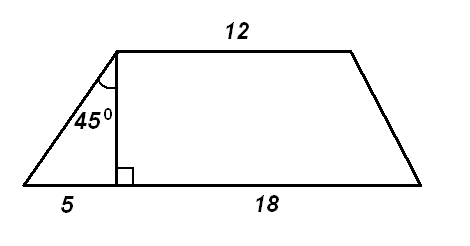
| 4. Найдите площадь трапеции, изображённой на рисунке.
| 
|
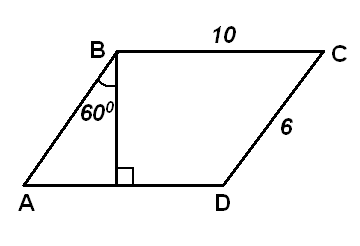
| 5. Найдите площадь параллелограмма, изображённого на рисунке.
| 
|
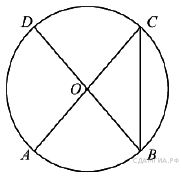
| 6. Величина центрального угла AOD равна 110°. Найдите величину вписанного угла ACB.
| 
|
| 7. Сторона ромба равна 26, а острый угол равен 60°. Высота ромба, опущенная из вершины тупого угла, делит сторону на два отрезка. Каковы длины этих отрезков?
| 
|
| 8. В равнобедренном треугольнике АВС с основанием АС внешний угол при вершине С равен 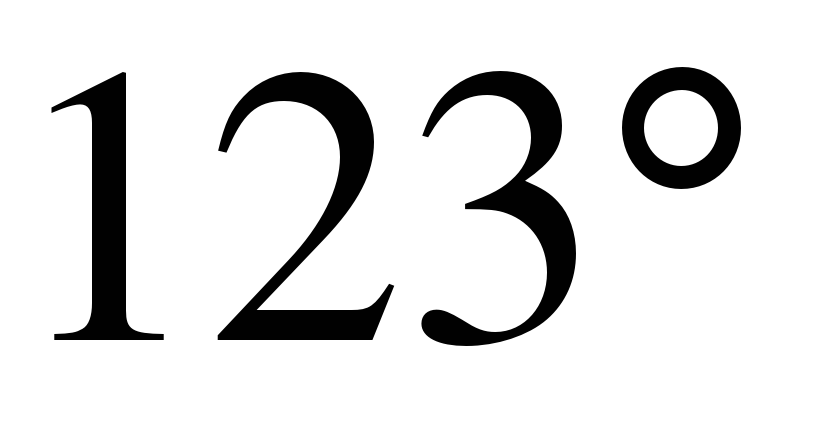 . Найдите величину угла ВАС. . Найдите величину угла ВАС. |
| 9. Найдите длину хорды окружности радиусом 13 см, если расстояние от центра окружности до хорды равно 5 см. Ответ дайте в см. |
| 10. В параллелограмме АВСD точка E — середина стороны AB. Известно, что EC=ED. Докажите, что данный параллелограмм — прямоугольник. |
| 11. В прямоугольном треугольнике ОАВ катет ОА равен 4, катет АВ равен 5. Найдите тангенс угла АОВ. |
| 12. Медианы ВК и ЕМ треугольника ВСЕ пересекаются в точке О. Докажите, что треугольники КОМ и ВОЕ подобны. |
| 13. Периметр равнобедренного тупоугольного треугольника равен 45 см, а одна из его сторон больше другой на 9 см.
Найдите боковую сторону треугольника. |
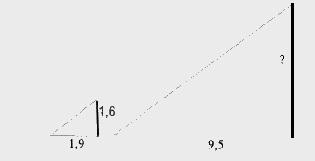
| 14. Длина тени громоотвода равна 9,5 м, в это же время вертикально воткнутый в землю кол высотой 1,6 м дает тень длиной 1,9 м. Найдите высоту громоотвода. Запишите ответ в виде целого числа или десятичной дроби.
| 
|
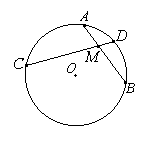
| 15. Хорды АВ и СD пересекаются в точке М, АМ = 4, ВМ = 6, МD = 2. Найдите CМ.
| 
|
| 16. В прямоугольном треугольнике АВС с прямым углом С известны катеты: АС=6, ВС=8. Найдите медиану СК этого треугольника. |
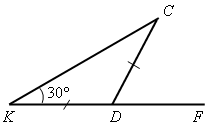
| 17. В равнобедренном треугольнике КDС угол СКD равен 30°. Найти внешний угол CDF.
| 
|
| 18. Основание АС равнобедренного треугольника АВС равно 12. Окружность радиуса 8 с центром вне этого треугольника касается продолжения боковых сторон треугольника и касается основания АС. Найдите радиус окружности, вписанной в треугольник АВС. |
| 19. В равнобедренной трапеции АВСD сторона АВ равна 4, высота ВН равна 2, угол ВАН равен 30°, основание ВС равно 6. Найдите площадь трапеции. |
| 20. Медианы ВК и ЕМ треугольника ВСЕ пересекаются в точке О. Докажите, что треугольники КОМ и ВОЕ подобны. |
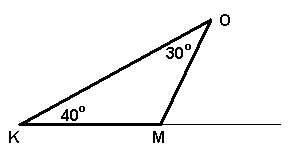
| 21. В треугольнике КОМ угол К равен 40°, угол О равен 30°. Найдите внешний угол при вершине М.
| 
|
| 22. Наклонная балка поддерживается тремя столбами, стоящими вертикально на равном расстоянии друг от друга. Длина двух меньших столбов 60см и 90см. Найдите длину большего столба. |
| 23. Прямоугольный газон обнесен изгородью длиной 30м. Площадь газона 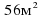 . Найдите длины сторон газона. . Найдите длины сторон газона. |
| 24. Вершина В ромба ABCD соединена с серединой стороны AD в точке К. Найдите площадь четырехугольника KBCD, если площадь ромба ABCD равна 28 см2. |
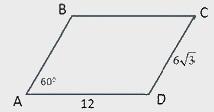
| 25. Найдите площадь параллелограмма АВСD, если угол А равен 60°, основание АD равно 12 см, а длина стороны DC равна 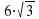 см. см.
| 
|
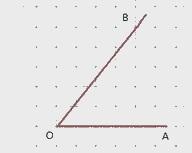
| 26. Найдите тангенс угла АОВ, изображенного на рисунке.
Найдите сумму градусных мер двух меньших углов этого треугольника.
| 
|
| 27. Из точки M, лежащей вне окружности, проведены две секущие МD и МВ. Длина ВА равна 16см, АМ - 2см, длина СМ равна 4см. Найдите длину секущей МD.
| 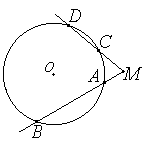
|
| 28. Треугольник АВС равнобедренный. ВF параллельна основанию треугольника АС. Докажите, что BF - биссектриса угла СВD.
|
|
| 29. В трапеции АВСD сторона АВ равна 5см, длина  равна 3см, длина основания ВС равна 6см, длина равна 3см, длина основания ВС равна 6см, длина  равна 4см. Найдите площадь трапеции АВСD. равна 4см. Найдите площадь трапеции АВСD. |
|
| 30. Найдите длину хорды окружности радиусом 13см, если расстояние от центра окружности до хорды равно 5см. |
| 31. Из точки А, лежащей вне окружности, проведены касательная АВ и секущая АD. Длина DC равна 9см, длина внешней части секущей СА равна 4см. Найдите длину касательной АВ.
|
|
| 32. В выпуклом четырехугольнике KLMN точки А, В, С, D - середины сторон KL, LM, MN, NK соответственно. Известно, что KL = 3. Отрезки АС и BD пересекаются в точке О. Площади четырехугольников KAOD, LAOB и NDOC равны соответственно 6, 6 и 9. Найдите площадь четырехугольника МСОВ. |