Задание 1. Тема и материал по теме

МИНОБРНАУКИ РОССИИ

Федеральное государственное бюджетное образовательное учреждение высшего образования

«Хакасский государственный университет им. Н.Ф. Катанова» (ФГБОУ ВО «ХГУ им. Н.Ф. Катанова»)

Институт естественных наук и математики

Кафедра математики, физики и информационных технологий

Направление подготовки 44.03.05 Педагогическое образование направленность (профили): математика, физика.

тема проекта:

ЯВЛЕНИЕ ИНТЕРФЕРЕНЦИИ

Выполнила: Овчиникова Виктория Сергеевна

Студент группы МФ-41, курс 4 Форма обучения очная

Абакан, 2024

Введение 3

1. Интерференция 5

1.2. Понятие когерентности 7

1.2.1. Временная когерентность 9

1.2.2. Пространственная когерентность 10

1.3. Интерференционная картина 11

1.3.2. Условия максимума и минимума 12

1.4. Интерференция в тонких пленках 14

Заключение 19

Библиографический список 20

Интерференция – одно из явлений волновой оптики, которое широко применяется в различных областях науки и техники.

Интерференция является фундаментальным физическим явлением, которое играет важную роль в оптике и создании оптических устройств.

Изготовление оптических фильтров и пленок с использованием интерференции позволяет получать материалы с точно заданными оптическими характеристиками, такими как спектральные характеристики, коэффициент пропускания или отражения света. Это открывает широкие возможности для создания новых оптических устройств с улучшенными свойствами и характеристиками.

Таким образом, изучение явления интерференции и его применения в изготовлении оптических фильтров и пленок представляет собой актуальную и перспективную тему, которая имеет большое значение для развития современных оптических технологий и их применения в различных областях науки и промышленности

В данной курсовой работе будет рассмотрено явление интерференции подробно, а также его применение в создании оптических фильтров и пленок.

Целью данной работы является анализ явления интерференции

Исследование данной темы позволит углубить знания в области оптики и оптических технологий, а также рассмотреть практическое применение интерференции в современных технологиях производства оптических устройств.

1. Интерференция

1. Открытие явления интерференции

Первый опыт по интерференции света наблюдал Гримальди. Опыт заключался в том, что на пути солнечного света установили экран с двумя близкими отверстиями (проделанные в ставне, закрывающие окно). Получаются два конуса световых пучков. Помещая экран там, где конусы накладываются друг на друга, Гримальди заметил, что в некоторых местах освещенность экрана меньше, чем если бы освещалось одним пучком. Из этого Гримальди сделал вывод о том, что не всегда сложение световых лучей будет увеличивать освещенность.

Другой опыт провел английский физик Роберт Гук. Изучая цвета мыльных пленок и тонких пластин слюды, он заметил, что цвета зависят от толщины мыльной пленки или слюдяной пластинки. Гук полагал, что свет - это колебательные движения, распространяющиеся в эфире, и что эти колебания являются поперечными. Явление интерференции света объяснялась тем, что световая волна, отражаясь от верхней и нижней поверхностей, например, мыльной пленки, попадает в глаз и производит ощущение различных цветов. Но у Гука не было представления о том, что такое цвет. Поэтому он не связывал цвет с частотой колебаний или длиной волны.

Следующий важный шаг в исследовании интерференции света в тонких пленках сделал Исаак Ньютон. Нужно измерять малые толщины порядка 1/10000мм, а устройств для этого тогда не было.

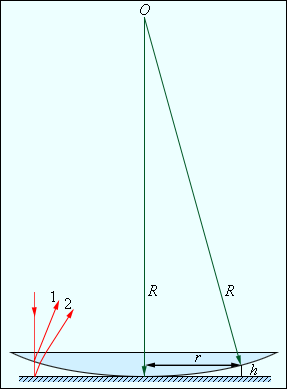
Рисунок 1. Установка Ньютона для интерференции света.

Обходя эту проблему, Ньютон кладет на плоскую стеклянную поверхность выпуклой стороной плоско выпуклую линзу (рис. 1). Тогда между нижней плоской и верхней выпуклой поверхностями образуется чрезвычайно тонкий слой воздуха, обнаруживающий яркие цвета; цветные кольца в белом свете и чередование одноцветных светлых и темных колец. За то, что интерференционная картина имела вид концентрических колец, она получила название колец Ньютона.

Самый знаменитый опыт по интерференции, он же и самый простой, это опыт Юнга по интерференции света от двух щелей. Юнг (1773—1829) понял, что нельзя ожидать интерференционных эффектов от двух независимых пучков света, и поэтому в 1807 г. он поставил следующий опыт. Он пропустил солнечный свет в темную комнату через отверстие, сделанное острой иглой, получив таким образом расходящийся пучок света. В середину пучка он поместил полоску бумаги шириной около миллиметра, которая разделила пучок на две части.

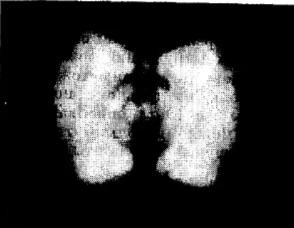
Рисунок 2. Интерференционные полосы, полученные способом Юнга.

Затем Юнг поместил на пути света экран и обнаружил на нем равноотстоящие полосы — в центре белую, а по краям окрашенные,— наложенные на френелеву дифракционную картину (рис.2). Когда он сдвигал полоску бумаги к краю первичного пучка, полосы исчезали. Юнг проделал и другие опыты, чтобы убедиться в том, что эффект возникает действительно вследствие расщепления первичного пучка [1].

Опыт Юнга стал доказательством справедливости волновой теории света. Также Юнг впервые ввел термин «интерференция».

1. Понятие когерентности

Интерференция света — явление, возникающее при сложении когерентных световых волн и состоящее в том, что интенсивность результирующей световой волны в зависимости от разности фаз складывающихся волн может быть больше или меньше суммы их интенсивностей, т. е. величин, пропорциональных квадратам амплитуд световых колебаний [2].

Итак, примем во внимание, что нужно различать два случая сложения двух колебаний одного периода:

1. Разность фаз колебаний сохраняется неизменной за время τ_ког, достаточное для наблюдений. Средняя энергия результирующего колебания отличается от суммы средних энергий

исходных колебаний и может быть больше или меньше неё в зависимости от разности фаз. В этом случае колебания называются когерентными. Сложение колебаний, при котором не имеет место суммирование интенсивностей, мы будем назвать интерференцией колебаний.

1. Разность фаз колебаний беспорядочно меняется за время наблюдения. Средняя энергия результирующего колебания равна сумме средних энергий исходных колебаний. Колебания в этом случае называются некогерентными. При их сложении всегда наблюдается суммирование интенсивностей, т.е. интерференция не имеет места.

Строго гармонические колебания одинаковой частоты всегда вполне когерентны между собой, ибо, поскольку они длятся, не обрываясь, имеющаяся у них разность фаз сохраняется без изменения долгое время. Поэтому при сложении таких гармонических колебаний всегда проявляется интерференция. [3]

Интерференция может происходить в случае негармонических колебаний, когда фаза каждого колебания является какой-то функцией времени, но их разность постоянна. Иными словами, возможно, что φ₁= φ₁(t), φ₂= φ₂(t), но φ1⁽t⁾– φ2⁽t⁾ = const. [4]

Условием интерференции одной и той же волн одной и той же частоты является их когерентность, т.е. сохранение неизменной разности фаз за время, достаточное для наблюдения. Способность когерентных волн к интерференции означает, что в любой точке, которой достигнут эти волны, имеют место когерентные колебания, которые будут интерферировать.

Когерентные световые волны можно получить, разделив (с помощью отражений или преломлений) волну, излучаемую одним источником, на две части. Если заставить эти две волны пройти разные оптические пути, а потом

наложить их одна на другую, наблюдается интерференция. Разность оптических длин путей, проходимых интерферирующими волнами, не должна быть очень большой, так как складывающиеся колебания должны принадлежать одному и тому же результирующему цугу волн (п. 1.2.1) [5].

Различают временную и пространственную когерентность.

1. Временная когерентность

Понятие временной когерентности можно связать с контрастом интерференционной картины, наблюдаемой в результате интерференции двух волн, исходящих из одной и той же точки поперечного сечения пучка (полученных методом деления амплитуд). Временная когерентность волны характеризует сохранение взаимной когерентности при временном отставании одного из таких лучей по отношению к другому. При этом мерой временной когерентности служит время когерентности — максимально возможное время отставания одного луча по отношению к другому, при котором их взаимная когерентность ещё сохраняется. Временная когерентность определяется степенью монохроматичности.

Временной аспект когерентности имеет исключительно важное значение при рассмотрении явлений взаимодействия электромагнитных волн ввиду того, что в строгом смысле на практике монохроматических волн и волн с абсолютно одинаковыми частотами не существует из-за статистического характера излучения электромагнитных волн. Монохроматические волны представляют собой бесконечный по продолжительности и локализации пространственно-временной процесс, что очевидно невозможно с точки зрения предположений о конечности энергии источников электромагнитных волн, а ввиду конечного времени излучения, его спектр также имеет ненулевую ширину.

Промежуток времени τ_ког, характеризующий допустимую временную задержку, в течение корой сохраняется когерентность, т.е. выполняется условие φ₁(t) - φ₂(t) = const, называется временем когерентности [4].

Можно сравнить фазы одного и того же колебания в разные моменты времени t₁ и t₂, разделённые интервалом τ_ког. Если негармоничность колебания проявляется в беспорядочном, случайном изменении во времени его фазы, то при достаточно большом τ_ког изменение фазы колебания может отклониться от гармонического закона. Это означает, что через время когерентности τ_ког гармоническое колебание «забывает» свою первоначальную фазу и становится некогерентным «само себе».

Для описания подобных процессов (а также процессов излучения конечной длительности) вводят понятие цуг волн — «отрезок» монохроматической волны, конечной длины. По истечении одного гармонического цуга он как бы заменяется другим с той же частотой, но другой фазой.

Для обычных (не лазерных) источников τ_ког равно по порядку величины 10^-9 – 10^-10 с.

Именно из такого значения τ_ког исходят при оценке очень важной физической величины – длины когерентности, т.е. расстояния L_ког = cτ_ког, на которое распространилась волна за время, пока её фаза и амплитуда оставались в среднем постоянными[4].

На практике монохроматические волны представляются в виде цугов конечной длительности по времени, представляющих собой гармонические во времени функции, ограниченные во времени и пространстве.

1. Пространственная когерентность

Пространственная когерентность — когерентность колебаний, которые совершаются в один и тот же момент времени в разных точках плоскости, перпендикулярной направлению распространения волны.

Понятие пространственной когерентности введено для объяснения явления интерференции (на экране) от двух разных источников (от двух точек удлиненного источника, от двух точек круглого источника и т. п.).

Так, при определённом расстоянии от источников разность оптического хода будет такой, что фазы двух волн будут отличаться. В результате этого приходящие волны от различных частей источника в центр экрана будут уменьшать значение мощности по сравнению с максимальным, которое имело бы место, если бы все волны имели одинаковую фазу. На расстоянии, где разность оптического хода приведёт к тому, что фазы двух волн будут различаться ровно на π, сумма двух волн будет минимальна.[6]

1. Интерференционная картина

Условия максимума и минимума. При наложении когерентных монохроматических световых волн происходит перераспределение светового потока в пространстве в виде закономерного чередования максимумов и минимумов интенсивности. Если на пути распространяющихся взаимодействующих лучей установить экран, то представленное чередование отразится на нем в виде интерференционной картины. Основные характеристики интерференционной картины — ширина полос интерференционной картины и видность.

Если сферические волны, идущие от двухточечных источников, взаимодействуют в дальнем поле, т. е. на большом расстоянии, то волны можно рассматривать как плоские. И интерференционная картина будет представлять собой параллельные (светлые и темные) полосы.

Если рассматривать взаимодействие волн в ближнем поле, то сферичностью волн пренебрегать нельзя. В этом случае, когда волны сферические, интерференционная картина будет представлять собой чередование темных и светлых концентрических окружностей.

Под оптической разностью хода двух лучей ∆ понимают разность оптических длин L₂ и L₁, проходимых этими лучами до точки наблюдения P. Так как

𝜔 2𝜋

с ⁼ с ⁼

2𝜋

,

𝜆₀

где 𝜔 = , λ₀ — длина волны в вакууме; с — скорость света в

𝑇

вакууме; T — период колебаний, то выражение для разности фаз имеет вид

2𝜋

δ = ∆ ,

𝜆₀

где ∆ = L₂ – L₁ — оптическая разность хода лучей.

Условие интерференционного максимума. Если оптическая (или геометрическая) разность хода лучей равна четному числу длин полуволн в вакууме

𝜆₀

Δ = ±2𝑚

2

⁽𝑚 = 0,1,2, … ⁾,

то разность фаз колебаний, приходящих в точку наблюдения, оказывается кратной 2π.

𝛿 = ±0,2𝜋, 4𝜋, … , 𝑚2𝜋 ⁽𝑚 = 0,1,2, … ⁾,

т. е. колебания в точке наблюдения от 2 источников будут происходить с одинаковой фазой. В этом случае суммарная интенсивность в точке наблюдения принимает значение

^{I = I1 + I2 + 2}√^{I1I2 .}

Условие интерференционного минимума. Если в оптической (или геометрической) разности хода лучей укладывается нечетное число полуволн в вакууме

∆ = ±(2m + 1) ^λ0

2

⁽m = 0,1,2, … ⁾,

то разность фаз колебаний оказывается кратной нечетному числу π

𝛿 = ±⁽2𝑚 + 1⁾𝜋.

В этом случае колебания в точке наблюдения находятся в противофазе.

Расстояние между интерференционными полосами — это расстояние между соседними максимумами (или минимумами).

Ширина интерференционной полосы — это расстояние между соседними минимумами интенсивности, которое имеет постоянное значение.

Зона интерференции — это область, в которой возникает система чередующихся максимумов и минимумов [2].

1. Интерференция в тонких пленках

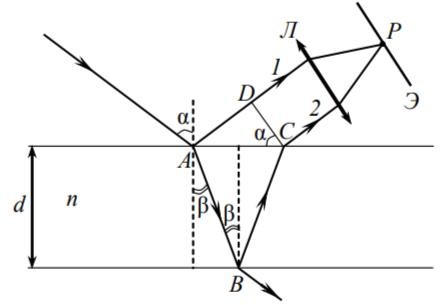
Рисунок 3. Интерференция в тонкой пленке (тонкой прозрачной пластинке).

Пусть на тонкую пленку (или на тонкую прозрачную пластинку) падает луч монохроматического света (рис. 3) под некоторым углом α. Падающий луч в точке падения А частично отражается и частично преломляется в пленке. Луч, отраженный от нижней поверхности пленки в точке В, выходит из пленки в точке С. Волновая поверхность CD перпендикулярна отраженным лучам 1 и 2. Эти лучи являются когерентными, поскольку образованы из одной световой волны. Лучи 1 и 2 фокусируются линзой Л на экране Э в точке P, в которой происходит интерференция. В результате интерференции в точке Р будет наблюдаться свет (если выполняется условие интерференционных максимумов) или темнота (если выполняется условие интерференционных минимумов). Результат интерференции можно наблюдать глазом. Поскольку лучи 1 и 2 параллельны друг другу, глаз должен быть аккомодирован в бесконечность. Оптическая разность хода лучей 1 и 2 равна:

∆ = 𝑛⁽AB + BC⁾ − AD − ^λ0,

2

где n – показатель преломления пленки, ^λ

2

– потеря полуволны при

отражении луча 1 от оптически более плотной среды.

При отражении световой волны от оптически более плотной среды фаза колебаний меняется на π радиан, что соответствует изменению разности хода

на ^λ . При этом в выражении для оптической длины пути следует добавить

2

(или вычесть) слагаемое ^λ . [2]

2

Из рис. 3 видно, что

𝐴𝐵 = 𝐵𝐶 =

𝑑

𝑐𝑜𝑠𝛽

; 𝐴𝐶 = 2𝑑 · 𝑡𝑔𝛽; 𝐴𝐷 = 𝐴𝐶 · 𝑠i𝑛𝛼 = 2𝑑 · 𝑡𝑔𝛽 · 𝑠i𝑛𝛼.

Тогда

∆= 𝑛

2𝑑

𝑐𝑜𝑠𝛽

λ₀

− 2𝑑 · 𝑡𝑔𝛽 · 𝑠i𝑛𝛼 −

2

2𝑑

= n

𝑐𝑜𝑠𝛽

2𝑑 · 𝑠i𝑛𝛽 · 𝑠i𝑛𝛼 λ₀

− − .

𝑐𝑜𝑠𝛽 2

Поскольку 𝑠i𝑛𝛼 = 𝑛 · 𝑠i𝑛𝛽, то

∆= 𝑛

2𝑑

𝑐𝑜𝑠𝛽

2𝑑 · 𝑛 · 𝑠i𝑛𝛽² λ₀

− −

𝑐𝑜𝑠𝛽 2

= 2d · n (

1 − 𝑠i𝑛𝛽² λ₀

cosβ ^{) −} 2

= 2d · n (

𝑐𝑜𝑠𝛽² λ₀

cosβ ^{) −} 2 ^.

Следовательно, оптическая разность хода лучей 1 и 2 равна

λ₀

∆= 2d · n · 𝑐𝑜𝑠𝛽 − ,

2

где d – толщина пленки, 𝛽 - угол преломления.

Учитывая, что 𝑐𝑜𝑠𝛽 = √1 − 𝑠i𝑛²𝛽, и выражая по закону преломления

s nβ = ^nα, получим ещё одну формулу для оптического разности хода лучей 1

n

и 2:

∆= 2𝑑^√𝑛² − 𝑠i𝑛²𝛼 − ^λ0.

2

Полосы равного наклона. На тонкую пленку толщиной d (d = const) падает рассеянный монохроматический свет (λ₀ = const). В рассеянном свете имеются лучи различных направлений, поэтому углы падения лучей

принимают значения от 0 до ^λ [7].

2

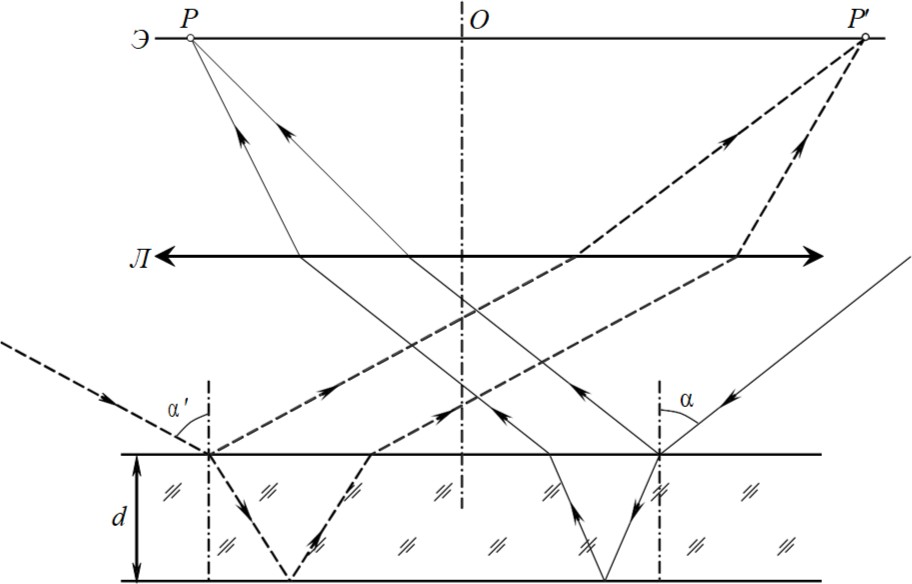
Рисунок 4. Интерференция рассеянного монохроматического света в тонкой пленке

с постоянной толщиной.

Покажем на чертеже (рис. 4) лучи, которые падают под некоторым углом 𝛼 и лежат в плоскости чертежа. Лучи, отраженные от верхней и от нижней поверхности пленки фокусируются собирающей линзой Л, в фокальной плоскости которой расположен экран Э. Освещенность в точке Р на экране будет определяться оптической разностью хода интерферирующих лучей. Лучи, которые идут в другой плоскости, но падают под тем же углом

𝛼, соберутся линзой в других точках экрана на таком же расстоянии от точки

О, что и точка Р. Таким образом, лучи рассеянного света, падающие под углом 𝛼, создадут на экране одну и ту же освещенность (по окружности или по дуге окружности с центром в точке О).

Лучи, падающие под другим углом 𝛼 , создадут на экране совокупность то- чек с другой освещенностью (т.к. оптическая разность хода интерферирующих лучей изменится).

Образуется окружность другого радиуса и другой освещенности. Для всей совокупности лучей на экране возникает система чередующихся светлых и темных круговых полос с центром в точке О. Интерференционная картина в этом случае называется полосами равного наклона, поскольку каждая полоса образована лучами, падающими на пленку под одинаковыми углами. В случае белого света интерференционная картина приобретает радужную окраску.[8]

Полосы равной толщины наблюдаются при интерференции света в случае отражения лучей от пленок переменной толщины или в клинообразных пластинках.

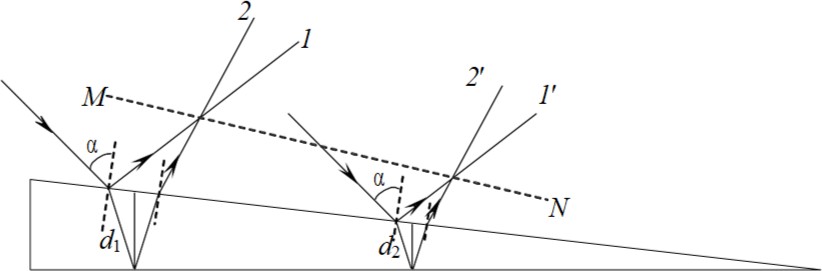
Рисунок 5. Интерференции монохроматического света в клинообразной пластинке.

Рассмотрим падение лучей монохроматического света на поверхность клинообразной пластинки под равными углами 𝛼 (рис. 5). Падающие лучи

частично отражаются от верхней поверхности клина, частично преломляются в клине и отражаются от его нижней поверхности, образуются когерентные лучи (лучи 1, 2 и 1′, 2′ на рис. 5). Разность хода лучей, интерферирующих в различных по толщине местах пленки, неодинакова. Эта разность остается постоянной вдоль линии, параллельной ребру клина, и убывает от основания к ребру. Отраженные лучи могут быть сфокусированы при помощи линзы, тогда на экране, расположенном в фокальной плоскости линзы, может наблюдаться интерференционная картина, которая представляет собой чередующиеся светлые и темные полосы. Каждая из таких полос образуется в результате отражения от участков клина с одинаковой толщиной d, поэтому интерференционная картина в этом случае называется полосами равной толщины

Контрольные вопросы.

1. При выдувании мыльного пузыря при некоторой толщине пленки он приобретает радужную окраску. Какое физическое явление лежит в основе этого наблюдения?

2. Какое выражение определяет понятие интерференции?

3. В данной точке среды возникает интерференционный максимум, если…

4. В данной точке среды возникает интерференционный минимум, если…

5. Интерференцию от двух ламп накаливания нельзя наблюдать, так как световые волны, излучаемые ими…

6. Две волны являются когерентными, если …

7. При каком времени запаздывания одного колебания по отношению к другому возникает максимальная результирующая интенсивность при их интерференции?

8. Два когерентных источника с длиной волны λ, расположены на разных расстояниях l1 и l2 от точки А В точке А наблюдается...

9. Две когерентные волны красного света λ = 760 нм достигают некоторой точки с разностью хода Δ = 2 мкм. Что произойдет в этой точке - усиление или ослабление волн?

10. Для просветления оптики на поверхность стекла с показателем преломления n1 наносят тонкую прозрачную пленку с показателем преломления n2. Каково соотношение между n1 и n2.

1. Г.Липтон. Великие эксперименты в физике. М., Мир, 1972

2. Оптика : учебное пособие / В. С. Акиньшин, Н. Л. Истомина, Н. В. Каленова, Ю. И. Карковский. — Санкт-Петербург : Лань, 2022. — 240 с. — ISBN 978-5-8114-1671-4. — Текст : электронный // Лань : электронно- библиотечная система. — URL: https://e.lanbook.com/book/211823 (дата обращения: 16.04.2024). — Режим доступа: для авториз. пользователей.

3. Ландсберг, Г. С. Оптика : учебное пособие / Г. С. Ландсберг. — 5-е изд., переработанное и дополненное. — Москва : «НАУКА», 1976. — 921 с.

4. Калитеевский, Н. И. Волновая оптика : учебное пособие / Н. И. Калитеевский. — 5-е изд. — Санкт-Петербург : Лань, 2022. — 480 с. — ISBN 978-5-8114-0666-1. — Текст : электронный // Лань : электронно- библиотечная система. — URL: https://e.lanbook.com/book/210113 (дата обращения: 16.04.2024). — Режим доступа: для авториз. пользователей.

5. Савельев, И. В. Курс общей физики : учебное пособие для вузов : в 5 томах / И. В. Савельев. — 6-е изд., стер. — Санкт-Петербург : Лань, 2022 — Том 4 : Волны. Оптика — 2022. — 252 с. — ISBN 978-5-8114-9198-8. — Текст : электронный // Лань : электронно-библиотечная система. — URL: https://e.lanbook.com/book/187737 (дата обращения: 17.04.2024). — Режим доступа: для авториз. пользователей.

6. Г. Колфилд. Оптическая голография = Handbook of Optical Holography (англ.) / С. Б. Гуревич. — М.: «Мир», 1982. — Vol. 1. [1] Архивная копия от 24 июня 2016 на Wayback Machine

7. Бутиков, Е. И. Оптика : учебное пособие / Е. И. Бутиков. — 3-е изд., доп. — Санкт-Петербург : Лань, 2022. — 608 с. — ISBN 978-5-8114-1190-0.

• Текст : электронный // Лань : электронно-библиотечная система. — URL: https://e.lanbook.com/book/210761 (дата обращения: 23.04.2024). — Режим доступа: для авториз. пользователей.

1. Рогачев, Н. М. Курс физики : учебное пособие / Н. М. Рогачев. — 3-е

изд., испр. и доп. — Санкт-Петербург : Лань, 2020. — 460 с. — ISBN 978-5-

8114-4076-4. — Текст : электронный // Лань : электронно-библиотечная система. — URL: https://e.lanbook.com/book/129235 (дата обращения: 23.04.2024). — Режим доступа: для авториз. пользователей.

1. Стафеев, С. К. Основы оптики : учебное пособие / С. К. Стафеев, К. К. Боярский, Г. Л. Башнина. — 2-е изд., испр. и доп. — Санкт-Петербург : Лань, 2022. — 336 с. — ISBN 978-5-8114-1495-6. — Текст : электронный // Лань : электронно-библиотечная система. — URL: https://e.lanbook.com/book/213251 (дата обращения: 24.05.2024). — Режим доступа: для авториз. пользователей.

2. Путилин, Э. С. Оптические покрытия : учебник / Э. С. Путилин, Л. А. Губанова. — Санкт-Петербург : Лань, 2022. — 268 с. — ISBN 978-5-8114- 2005-6. — Текст : электронный // Лань : электронно-библиотечная система.

• URL: https://e.lanbook.com/book/212309 (дата обращения: 27.05.2024). — Режим доступа: для авториз. пользователей.

1. Петров, В. М. Интерференция и дифракция для информационной фотоники : монография / В. М. Петров, А. В. Шамрай. — 2-е изд., стер. — Санкт-Петербург : Лань, 2020. — 460 с. — ISBN 978-5-8114-5151-7. — Текст

: электронный // Лань : электронно-библиотечная система. — URL: https://e.lanbook.com/book/133481 (дата обращения: 27.04.2024). — Режим доступа: для авториз. пользователей.

Калитеевский, Н. И. Волновая оптика : учебное пособие / Н. И. Калитеевский. — 5-е изд. — Санкт-Петербург : Лань, 2022. — 480 с. — ISBN 978-5-8114-0666-1. — Текст : электронный // Лань : электронно- библиотечная система. — URL: https://e.lanbook.com/book/210113 (дата обращения: 27.04.2024). — Режим доступа: для авториз. пользователей