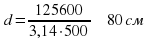МБОУ «Средняя общеобразовательная школа №44» Школьная научно-практическая конференция
школьников «Первые шаги»
Секция «Математика и информатика»
Загадочное число 
Автор работы: Киселева Татьяна Вадимовна,
ученица 7 «Б» класса Руководитель: Холодова Ирина Владимировна,
учитель математики.
Кемерово 2014
Содержание:
1. Введение……………………………………………………………………………………………………… 3
2. Как все начиналось? ………………………….................................................4
3. Загадочное число «Пи» ...................................................................................5
4. Каким приближением числа « Пи» владели люди? …………………………………..6
5. Вездесущность числа « Пи»………………………………………………………………………….9
6. Международный день числа «Пи»……………………………………………………………. 11
7. Практическое применение числа «Пи»..........................................................14
8. Заключение…………………………………………………………………………………………………. 16
9. Литература…………………………………………………………………………………………………… 17
2
Введение.
«Куда бы мы ни обратили свой взор, мы видим проворное и трудолюбивое число π : оно заключено и в самом простом колесике, и в самой сложной автоматической машине.»
Кымпан Ф.
Число π является одним из интереснейших чисел, встречающихся при изучении математики. Оно встречается и в других школьных дисциплинах. Нет в математике более загадочного и мистического числа, чем число "пи". Несмотря на то, что о нем было известно далеко в древности, но до сих пор оно будоражит умы не только ученых, но и простых людей. С этим числом связано множество интересных фактов и рекордов. В школьной программе это число применяется достаточно часто, но вряд ли кто - то из учеников серьезно задумывается над историей и над тайнами числа "пи". Эта работа даст возможность исследовать загадку числа "пи".
Основополагающий вопрос. Что это такое ?
?
Проблемные вопросы. В чем тайна числа  ?
?
Цель и задачи этой работы состоят в том, чтобы на историческом материале показать важность и необходимость проблемы вычисления числа , раскрыть вездесущность геометрического символа, а также показать огромное трудолюбие и работоспособность ученых, занимающихся этим вопросом в течение многих столетий. Расширить и углубить представление о практическом значении и применении математических понятий в окружающем нас мире.
, раскрыть вездесущность геометрического символа, а также показать огромное трудолюбие и работоспособность ученых, занимающихся этим вопросом в течение многих столетий. Расширить и углубить представление о практическом значении и применении математических понятий в окружающем нас мире.
Задачи:
а) Познакомиться с историей этого числа;
б) Узнать, сколько знаков имеет после запятой число π;
в) Отыскать материал о роли  в жизни человека.
в жизни человека.
г) Найти интересные факты о числе π.
д) Выяснить, как появился день числа π.
е) Решить задачи, связанные с числом 
Методы. Сбор, анализ, систематизация и обобщение полученной информации из литературы, интернет ресурсов.
Этому числу удавалось в течении тысячелетий держать в плену мысли и чувства не только математиков и астрономов, но и философов и художников.
3
1. Как все начиналось?
История числа. «В начале сотворил Бог небо и землю.» Бытие 1:1. «Он(Соломон) выстроил круглый бассейн из литого металла размерами десять мер от обода до обода (диаметр=10) и пять мер высотой. Это дало линию вокруг тридцать мер длиной». Письменная история числа начинается с египетского папируса, датируемого примерно 2000 годом до нашей эры, но оно было известно ещё древним людям. Число обратило на себя внимание людей ещё в те времена, когда они не умели письменно излагать ни своих знаний, ни своих переживаний, ни своих воспоминаний.
Открывателями числа π можно считать людей доисторического времени, которые при плетении корзин заметили, что для того, чтобы получить корзину нужного диаметра, необходимо брать прутья в 3 раза длиннее его. Найдены таблички из обожженной глины в Месопотамии, на которых зафиксирован данный факт. Как считают специалисты, число π было впервые открыто вавилонскими магами. Оно использовалось при строительстве знаменитой Вавилонской башни, история которой вошла в Библию. Однако недостаточно точное исчисление ими π привело к краху всего проекта. Считается также, что число π лежало в основе строительства знаменитого Храма царя Соломона.
Пи (π) - буква греческого алфавита, применяемая в математике для обозначения отношения длины окружности к диаметру. Это обозначение (вероятно, от греч. perijereia окружность, периферия) стало общепринятым после работы Л. Эйлера, относящейся к 1736, однако впервые оно было употреблено английским математиком) Уильямом Джонсом (1706). Как и всякое иррациональное число π представляется бесконечной непериодической десятичной дробью: π = 3,141592653589793238462643...
Теперь мы знаем многое об этом числе: оно иррациональное, т. е. его нельзя представить в виде отношения натуральных чисел – оно может быть выражено бесконечной десятичной непериодической дробью;
оно трансцендентно, т. е. не может быть корнем алгебраического уравнения с рациональными коэффициентами и натуральными показателями у переменной.
Число «Пи» в науках. Алгебра: π - иррациональное и трансцендентное число.
Тригонометрия: радианное измерение углов.
Планиметрия: длина окружности и её дуги; площадь круга и его частей.
4
Стереометрия: объем шара и частей; объем цилиндра, конуса и усеченного конуса; площадь поверхности цилиндра, конуса и сферы.
Физика: теория относительности; квантовая механика; ядерная физика.
Теория вероятностей: формула Стирлинга для вычисления факториала.
Кроме этого, в астрономии, космонавтике, архитектуре, навигации, электронике и мн.др.
2. Загадочное число «Пи».
Абсолютно все знают, что такое "пи". Но знакомое всем со школы число возникает во многих ситуациях, не имеющим никакого отношения к окружностям. Его можно встретить в теории вероятностей, в формуле Стирлинга для вычисления факториала, в решении задач с комплексными числами и прочих неожиданных и далеких от геометрии областях математики. Английский математик Август де Морган назвал как-то "пи" “…загадочным числом 3,14159…, которое лезет в дверь, в окно и через крышу.
14 марта 2011 года исполнилось ровно 250 лет с того дня, как немецкий физик и математик Иоганн Генрих Ламберт, отвлекшись от своих трактатов по оптике и астрономии, доказал, что Пи является иррациональным числом. Это значит, что не существует таких целых чисел p и q, для которых было бы верно равенство Пи = p/q.
На первый взгляд, что здесь такого важного? Рациональное число или иррациональное - какая разница? В практическом инженерном применении это ничего не меняет, потому что при конструкции любого цилиндра или хирургической иголки они все равно аппроксимируют Пи с погрешностью, допустимой для каждой конструкции. Это могли делать инженеры Римской империи почти так же успешно, как мы, оснащенные мощной компьютерной техникой. Теперь мы знаем, что число Пи иррационально – оно может быть выражено бесконечной десятичной непериодической дробью
Изучением числа Пи занимались многие математики всех времен и народов. Столь внимательное отношение к числу Пи не случайно. Это число играет важную роль в математике, физике, астрономии, технике и других науках, многих практических расчётах. Действительно, без знаний о числе Пи нельзя вычислить длину окружности, площадь круга, площади поверхностей
5
и объёмы круглых тел, выполнить многие расчёты в электротехнике и радиотехнике, астрономии и космонавтике. Можно с полной уверенностью утверждать, что по характеру и полноте знаний о числе Пи возможно судить о научно-техническом уровне развития данного общества.
3. Каким приближением числа π владели люди?
В истории математики считается, что первое вычисление на основе строгих теоретических рассуждений было выполнено выдающимся математиком древности Архимедом. В своём труде «Об измерении круга» он доказал, что 3 10/71
Примерно такое же представление о числе характерно для математиков древней Азии. В индийских “сутрах” (VII-V вв.до н.э.) принимается значение числа Пи, равное 3,008. Значительно позже Ариабхатта (Vв) и Бхаскара (XII в) в качестве Пи брали значение 62832/20000, т.е. 3,1416…, Брахмагупта (VI- VIIв), Магавира (IXв) и Сриддхара (XIв)- значение 3,162…; астроном Ван Фань (229-267 г.) считал , что Пи=142/45, т.е. 3,155…; Цзу Чун-чжи (428-499 г.) считал “точным” значением Пи=355/113.
Проблеме Пи-4000 лет. Исследователи древних пирамид установили, что частное, полученное от деления суммы двух сторон основания на высоту пирамиды, выражается числом 3,1416. В знаменитом папирусе Ахмеса приводится такое указание для построения квадрата, равного по площади кругу: «Отбрось от диаметра его девятую часть и построй квадрат со стороной, равной остальной части, будет эквивалентен кругу». Из этого следует, что у Ахмеса Пи≈3,1605. Так началась письменная история числа Пи.
В XV в. Иранский математик ал-Каши нашел значение Пи с 16-ю верными знаками. Адриан Ван Ромен ( из Бельгии ) в XVIв. С помощью 230 угольников получил 17 верных десятичных знаков , а голландский вычислитель-Лудольф ван-Цейлен( 1540-1610), вычисляя Пи получил 35 верных знаков. Учёный обнаружил большое терпение и выдержку, несколько лет затратив на определение числа Пи. В его честь современники назвали Пи-«Людольфово число ». Согласно завещанию на его надгробном камне было высечено найденное им значение Пи.
6
Самой важной, можно сказать, переломной датой в истории числа Пи был 1882 г., когда немецкий математик Карл Линдеман окончательно установил таинственный характер этого знака: число Пи не может быть корнем алгебраического уравнения с рациональными коэффициентами, т.е. оно трансцендентно.
Самым неутомимым вычислителем Пи был английский математик Уильям Шенкс. Более 20 лет жизни он посвятил вычислению 707 знаков числа Пи. К сожалению, он ошибся в 520-м знаке и все последующие цифры неверны. (Ошибку обнаружили лишь в 1945г).
С появлением ЭВМ значение числа Пи было вычислено с достаточно большой точностью. В США был получен результат с более 30млн. знаков. Вычисление такого числа знаков для Пи не имеет практического значения, а лишь показывает огромное преимущество и совершенство современных средств и методов вычисления по сравнению со старыми. Филипп Дж.Девис писал в своей книге: «Загадочное и чудесное Пи стало чем-то вроде покашливания, которым вычислительные машины прочищают горло».
Учёные Токийского университета сумели поставить мировой рекорд в вычислениях числа Пи до 1241триллионного знака. Для этого группе программистов и математиков, которую возглавлял профессор Ясумаса Канада, понадобилась специальная программа, суперкомпьютер и 400 часов машинного времени.
Погоня за знаками числа.
На протяжении всей истории изучения числа  , вплоть до наших дней, велась своеобразная погоня за десятичными знаками этого числа.
, вплоть до наших дней, велась своеобразная погоня за десятичными знаками этого числа.
• Леонардо Фибоначчи (около 1220г.) - три первых
точных знака числа
• Андриан Антонис -6 точных десятичных знаков (в XVI в.)
• Цзу Чун-чжи (Китай) – 7 десятичных знаков (V в.н.э.);
• Франсуа Виет – 9 десятичных знаков;
• Андриан ван Ромен – 15 десятичных знаков (1593г.);
• аль-Каши – 17 знаков после запятой (XV в.)
• Лудольф ван Цейлену – 32 десятичных знаков (1596г.);
• Авраам Шарп – 72 десятичных знаков
• Джон Мечин – 100 десятичных знаков (1706 г.)
• З. Дазе – 200 десятичных знаков (1844г.)
• Т. Клаузен – 248 десятичных знаков (1847г.) 7
Зачем они это делают? Во-первых, для очень точных вычислений какой-нибудь орбиты спутника желательно иметь этих знаков побольше, а то можно и в Луну не попасть. Да и для строительства плотин и гигантских мостов тоже нужна точность. А во-вторых, это число имеет собственную научную ценность. В процессе вычислений этих самых знаков было открыто множество разных методов и целых наук. Но самое главное в десятичной части числа Пи нет повторений, как в обычной периодической дроби, а число знаков после запятой у него бесконечно. На сегодняшний день проверено, что в 500млрд. знаков числа Пи повторений действительно нет. Есть основания полагать, что их нет вообще.
Три первые цифры числа = 3,14… запомнить совсем несложно. А для запоминания большего числа знаков существуют забавные поговорки и стихи. Например, такие:
- « Что я знаю о кругах» (3,1416 ) ; - «Это я знаю и помню прекрасно «пи» многие знаки мне лишни, напрасны»
(3,14159265358..) .
Значение первых чисел в числе Пи впервые правильно рассчитал одни из величайших математиков древнего мира, Архимед из Сиракуз (род.287 – ум.212 г. до н. э.). Он представил это число в виде нескольких дробей. По легенде, Архимед был настолько увлечён расчетами, что не заметил, как римские солдаты взяли его родной город Сиракузы. Когда римский солдат подошел к нему, Архимед закричал по-гречески: «Не трогай моих кругов!». В ответ на это солдат заколол его мечом. О чем в стихах сообщил нам замечательный писатель С.Бобров в своей книге «Волшебный Двурог».
| Гордый Рим трубил победу
Над твердыней Сиракуз;
Но трудами Архимеда
Много больше я горжусь. Чтобы нам не ошибаться, Надо правило прочесть: Три, четырнадцать, пятнадцать, Девяносто два и шесть. |
Надо только постараться И запомнить все как есть: Три, четырнадцать, пятнадцать, Девяносто два и шесть. Три, четырнадцать, пятнадцать, Девять, два, шесть, пять, три, пять. Чтоб наукой заниматься Это каждый должен знать. |
Для простого бытового использования этих знаков уже достаточно. Но неутомимые учёные продолжали и продолжали вычислять десятичные знаки числа Пи.
8
4. Вездесущность числа Пи.
О вездесущности числа Пи рассказывается в книге «Загадочная биография Земли». В этой книге рассказывается об идеях и исследованиях кандидата географических наук В. Пиотровского. Ему удалось установить, что в классификации рельефа можно выделить 15 порядков. Экспериментальным путем он установил, что все структуры земного рельефа от мелких до гигантских связаны между собой через число π.( три с небольшим). Анализируя контуры знаменитых скрипок Амати, Гварнери, Страдивари, он установил, что можно выделить некий объём воздуха в корпусе скрипки. Этот “шар” ровно 3 раза укладывается в двух резонаторах инструмента. Это оказалось верно для всех трёх мастеров. Конструируя скрипки, старые мастера делали их не меньше и не больше определенного размера: посредине “эталонный объём” и три таких объёма вправо и влево.
Опять три! Может 3,14? А вот для рояля, балалайки и гитары присутствие “тройки” не обнаружено. Но эти инструменты и звучат тихо: это камерные инструменты.
В.Пиотровский обратил внимание на эфы скрипки - отверстия в её верхней крышке, напоминающие по форме латинскую букву S. Именно эти отверстия дают выход звукам, рождающимся во внутреннем объёме скрипки. Они как бы снимают большую часть звуковой энергии. В гитаре и балалайке эту же роль выполняют круглые отверстия.
При изучении архитектуры церкви В.Пиатровский обнаружил, что объём купола храма примерно 3 раза укладывается во всём объёме храма. Самые звучные и певучие колокола отлиты русскими мастерами. Профиль контура русского колокола имеет вид равнобедренного треугольника. Пока только предполагают, что углы колокола близки по величине к радиану. А это- окружность, делённая на 2. И опять появляется это магическое число!
Оно впрямь магическое. Член - корреспондент А. И. Звонков отмечает интересную закономерность у всех растений с овальной формой листьев. Если мысленно разделить лист, например липы, по линии его наибольшей ширины, то левая часть составит примерно 1\3 всей длины. Кривая полета снаряда, зависимость скорости горения пороха от давления, распределение молекул газообразного кислорода в зависимости от различной температуры, пульсовые колебания стенок артерий – все эти явления подтверждают общую закономерность: на этих кривых линия наибольшего подьема делит их абсциссу в отношении 1:2. Не правда ли, интересные соотношения.
9
В процессе измерений размеров Великой пирамиды в Гизе оказалось, что она имеет такое же соотношение высоты к периметру своего основания, как радиус окружности к ее длине, то есть 1/2π.
Если рассчитать длину экватора Земли с использованием числа π с точностью до девятого знака, ошибка в расчетах составит около 6 мм.
Инопланетяне и число «Пи»
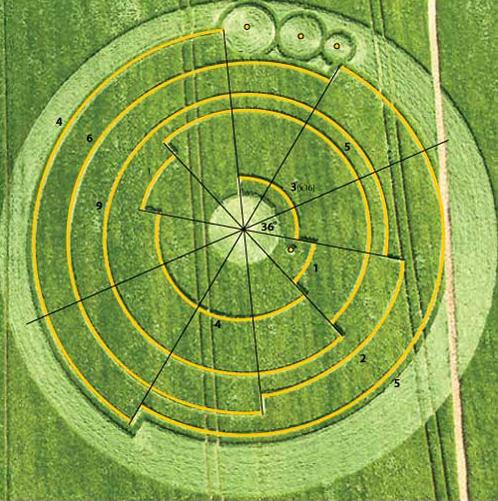
Вполне очевидно, что о роли числа «Пи» знают и представители высокоразвитых внеземных цивилизаций. Это может подтвердить случай, произошедший в 2009 году, когда примерно в 130 километрах от Лондона на полях в графстве Уилтшир (Wiltshire), около местечка Barbury Castle появились загадочные знаки.
Рядом с этим полем сохранились остатки построек древней доримской эпохи. На поле появился рисунок из полегших колосьев. Астрофизик из США Михаэль Рид (Michael Reed) смог прочитать этот узор и увидел, что в нем зашифровано число «Пи» с точностью до 9 знаков после запятой. Результат этой расшифровки просто очевиден и понятен и доступен даже людям, далеким от математики и геометрии.
10
Михаэль Рид вспоминает: «Сначала это показалось мне забавным. Я продолжил. За дугой из четырех секторов - после очередной ступеньки - оказалась дуга в один сектор. Затем в пять, в девять, в два, и так далее
В результате получилось 3.141592654 - это число "Пи" с точностью до девятого знака! И кому понадобилось об этом сообщить? Выходит, что инопланетяне дают нам знать о возможностях загадочного числа «Пи», лежащего в основе мироздания. Значит, даже они считают это число основой всей жизни во Вселенной.
Вычисления японского профессора Ясумаса Канада, который недавно определил число πи до 12411-триллионного знака после запятой, были тут же засекречены - с таким объемом данных не составляет труда воссоздать содержание любого секретного документа, правда этих данных недостаточно для определения местонахождения любого человека, для этого необходимо как минимум 236734-триллионов знаков после запятой. Многие аналитики предполагают, что такие работы сейчас ведутся в Пентагоне.
Вадим Косогоров на конференции в Абу-Даби озвучивает мысль о наличии интеллекта у числа π. Вот его слова: «Число π само себя контролирует, оно разумно! Каким образом число вообще может быть разумным? Да очень просто. Человеческий мозг содержит 100 млрд. нейронов, число знаков π после запятой вообще стремится к бесконечности, в общем, по формальным признакам оно может быть разумным».
Почему числу «Пи» уделяется такое внимание?
Считается, что если правильно просчитать все знаки числа, то откроется множество тайн мировоздания. Именно поэтому многие и интересуются числом «пи».
В одной книге говорится: «Число π захватывает умы гениев науки и математиков-любителей во всем мире». Некоторые даже считают его одним из пяти важнейших чисел в математике.
Число π появляется в формулах, используемых во многих сферах. Физика, электротехника, электроника, теория вероятностей, строительство и навигация - это лишь некоторые из них. И кажется, что подобно тому, как нет конца знакам числа π, так нет конца и возможностям практического применения этого полезного, неуловимого числа π.
11
5. Международный день числа Пи
День числа пи отмечается любителями математики 14 марта в 1:59:26.
Этот неофициальный праздник придумал в 1987 году физик из Сан-Франциско Ларри Шоу (Larry Shaw), который подметил, что в американской системе записи дат (месяц / число) дата 14 марта — 3/14 — и время 1:59:26 совпадает с первыми разрядами числа π = 3,1415926….
Обычно празднуют в 1:59:26 дня (в 12-часовой системе), но придерживающиеся 24-часовой системы считают, что в этот момент время 13:59, и предпочитают отмечать ночью.
В это время читают хвалебные речи в честь числа π, его роли в жизни человечества. Рисуют антиутопические картины мира без π. Пекут и едят «пи-рог» («pie») с изображением греческой буквы «пи» или с первыми цифрами самого числа. Пьют напитки и играют в игры, начинающиеся на «пи», решают математические головоломки и загадки, водят хороводы вокруг предметов, связанных с этим числом.
Популярность числу π придаёт и то, что оно совпадает с Днём рождения великого физика Альберта Эйнштейна.
Ещё одной датой, связанной с числом π, является 22 июля, которое называется «Днём приближённого числа Пи» (англ. Pi Approximation Day), так как в европейском формате дат этот день записывается как 22/7, а значение этой дроби является приближённым значением числа π.
Существуют и Пи-клубы, члены которого, являясь фанатами загадочного математического феномена, собирают все новые сведения о Пи и пытаются разгадать его тайну. Чтобы вступить в него, для начала надо вызубрить наизусть как можно большее количество чисел Пи после запятой.
Выход нового диска Кейт Буш "Aerial" заставил сердца математиков забиться сильнее. В 2005 году певица Кейт Буш выпустила песню « Пи». В ней прозвучали 124 цифры из знаменитого числового ряда 3,141…. Хотя Кейт Буш вряд ли примут в клуб фанатов Пи. В ее песне неправильно названо 25-е число последовательности, да и потом исчезли куда-то целых 22 цифры.
Пи заворожило не только Кейт Буш. Германский король Фридрих Второй был настолько очарован этим числом, что посвятил ему… целый дворец Кастель дель Монте, в пропорциях которого можно вычислить Пи. Сейчас волшебный дворец находится под охраной ЮНЕСКО. 12
Рекорд запоминания числа Пи принадлежит украинцу Андрею Слюсарчуку, который запомнил 30 миллионов знаков числа после запятой. Поскольку простое перечисление этого заняло бы целый год, то судьи проверяли Слюсарчука следующим образом - они просили его назвать произвольные последовательности числа Пи с любого из 30 миллионов знака. Сверялся ответ по 20-томной распечатке.
В 1998 году режиссером Дарреном Арновски был снят психологический триллер, который так и назывался - "Pi ".В фильме рассказывается про таланливого математика, который пытался найти и расшифровать универсальный цифровой код, согласно которому изменяются все биржевые сводки.
В Лейпциге было обнаружено таинственное яйцо с нанесенными на нем 2345 цифрами числа пи.
Аромат духов назван в честь загадочного числа «пи». Этот аромат был создан под руководством Александра МакКуина - коренного англичанина, жившего в Париже.
Флакон аромата - отдельное произведение искусства. Он был создан знаменитым дизайнером Сержем Мансо и представляет собой прозрачную пирамиду с вытесненными геометрическими узорами.
13
7. Практическое применение числа Пи.
1. Числовой фокус китайского астронома Цю-Шунь-Ши.
Напишем по два раза три нечетных числа:
1, 1, 3, 3, 5, 5.
Три последних числа сделаем числителем, а три первых знаменателем дроби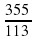 Эта дробь позволяет вычислить
Эта дробь позволяет вычислить  с точностью до седьмого знака.
с точностью до седьмого знака.
2. Задача:
Колесо на расстоянии 1256 м сделало 500 оборотов.
Найдите диаметр колеса (π ≈ 3,14).
Ответ дайте в сантиметрах
Решение: 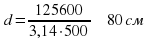
3. Число π в литературе
Геометрия знает немало поучительных и необычных задач. Одна из них описана в романе Жюля Верна, герой которого подсчитывал, какая часть его тела прошла более длинный путь за время его кругосветных странствий – голова или ступни ног.
Приведём решение этой задачи.
Ноги прошли путь 2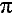 R, где R – радиус земного шара. Верхушка же головы прошла при этом 2
R, где R – радиус земного шара. Верхушка же головы прошла при этом 2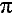 (R + 1,7), где 1,7 м – рост человека. Разность путей равна 2
(R + 1,7), где 1,7 м – рост человека. Разность путей равна 2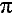 (R + 1,7) - 2
(R + 1,7) - 2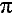 R = 2
R = 2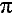 • 1,7 = 10,7 м. Итак, голова прошла путь на 10,7 м больше, чем ноги.
• 1,7 = 10,7 м. Итак, голова прошла путь на 10,7 м больше, чем ноги.
Любопытно, что в окончательный ответ не входит величина радиуса земного шара. Поэтому результат получится одинаковый и на Земле, и на Юпитере, и на самой мелкой “планетке”. Вообще, разность длин двух концентрических окружностей не зависит от их радиусов, а только от расстояния между ними.
Прибавка одного сантиметра к радиусу земной орбиты увеличила бы ее длину ровно настолько, насколько удлинится от такой же прибавки радиуса окружность пятака.
На этом геометрическом парадоксе и основана любопытная задача: “Если обтянуть земной шар по экватору проволокой и затем прибавить к ее длине 1 м, то сможет ли между проволокой и землей проскочить мышь?”
Обычно отвечают, что промежуток будет тоньше волоса: что значит один метр по сравнению с 40 миллионами метров земного экватора! В действительности же величина промежутка равна 100см/2 π приблизительно 16см. Не только мышь, но и крупный кот проскочит в такой промежуток!
14
4. Диаметр циферблата Кремлевских курантов 6,12 м. Длина минутной стрелки 2,54 м. Найдите площадь циферблата.
Решение: R = 6,12 : 2 = 3,06 ; r = 2,54 ; S = πR2- πr2 = π(R2 – r2); S ≈ 9м2
5. Спутник вращается по круговой орбите на высоте 100км от поверхности Земли. Какова длина пути, проходимого спутником за 8 оборотов вокруг Земли?
Решение: радиус Земли - 6371км, R = 6371+100 = 6471; C = 2πR ; C = 2× 3,14× 6471×8≈ 325104 ; C=325103км.
6. Задача. Контур нижней части этой вазы образован дугой в 3/4 окружности диаметром 10см. Верхняя половина ограничена тремя четвертушками той же окружности. Как быстро можно назвать с точностью до последнего десятичного знака длину стороны квадрата, имеющего площадь, равную площади этой фигуры?
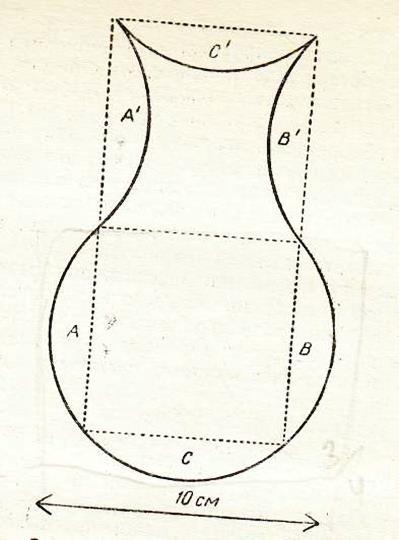
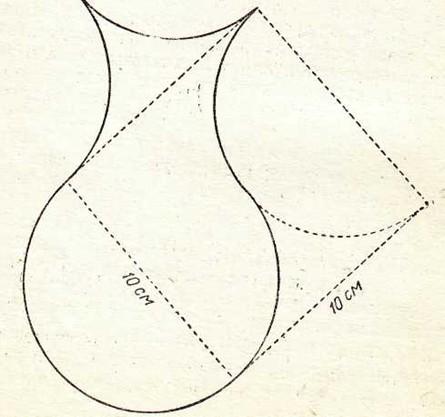
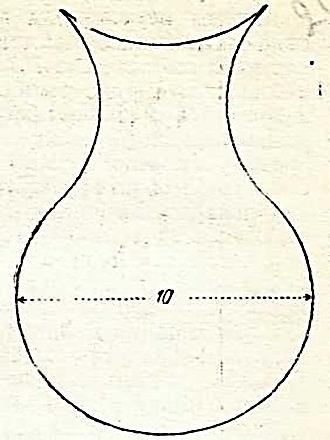
Рис 1 рис 2 рис 3
Ответ: сторона квадрата также равна 10см. Если пунктирные линии провести так, как показано на рисунке, то станет видно, что сегментами А, В, и С можно заполнить «лунки» А1, В1 и С1, при этом образуются два квадрата общей площадью 100см2. На рисунке показано, как разрезать вазу всего лишь на три части так, чтобы из них можно было сложить квадрат 10×10 см.
15
8. Заключение.
В своей работе я подробнее познакомилась с числом π – одной из вечных ценностей, которой человечество пользуется уже много веков. Узнала некоторые аспекты его богатейшей истории. Загадка таинственного числа π не разрешена вплоть до сегодняшнего дня, хотя по-прежнему волнует ученых. Проанализировав все эти данные, я поняла, что число “Пи” одно из интереснейших чисел в математике. Являясь темой изучения в школах, университетах, академиях и прочих учебных заведениях, оно также незаменимо в жизни. Изучив теоретический материал, я узнала много нового о числе Пи. Например, то что у числа Пи есть свой день, который считают днём рождения. Я познакомилась с неутомимыми учёными, которые потратили огромное количество сил, времени и терпения на определение количества знаков после запятой в записи числа Пи.
Любой школьник сегодня должен знать, что обозначает и чему приближенно равно число «пи». Ведь у всех первое знакомство с числом π, использование его при вычислении длины окружности, площади круга происходит в 6 классе. Но, к сожалению, эти знания остаются для многих формальными и уже через год – два мало кто помнит не только то, что отношение длины окружности к её диаметру одно и то же для всех окружностей, но даже с трудом вспоминают численное значение числа, равное 3,14. В своей работе я попробовала приподнять завесу богатейшей истории числа, которым человечество пользуется уже много веков. Моя работа оказалась увлекательной и познавательной, и самое главное, столько еще неизведанного, неизвестного о числе π, что работу можно продолжать.
16
9. Литература.
1. Жуков А. В. Вездесущее число π. 2004.
2. Энциклопедический словарь юного математика.
3. Друянов В. Загадочная биография Земли.
4. Математика. «Первое сентября» №27-28, 1993; №8,1997.
5. Глейзер Г. История математики в школе. 1982.
Интернет ресурсы
http://encyclopedia.dekanat.ru
http://www.lexicon.org.ua/ojegov/p/95493.html
http://www.school.mipt.ru/Default.asp?Root=156
http://planetatain.ru/bloq/misticheskoe chislo pi/2013-09-20-6144#ixzz2sGWOiDaB
http:// ukrday.com/zhizn/
http:// Wikipedia.org
17








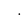

 Эта дробь позволяет вычислить
Эта дробь позволяет вычислить