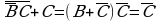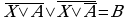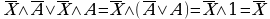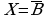8 класс Тема 1. 2. Законы логики Общая цель урока: сформулировать законы математической логики, научиться преобразовывать логические выражения, используя логические законы.
Опорные понятия, используемые в процессе урока:
- логика, логические операции, логические выражения
Новые понятия, используемые в процессе урока:
- законы логики, формализация.
Решаемые учебные задачи:
- Познакомить учащихся с законами математической логики; сформулировать правила преобразования логических выражений;
- научить учащихся приводить логическое выражение к нормальной форме;
- Развитие логического мышления.
Средства ИКТ, используемые на уроке:
• персональный компьютер (ПК) учителя, мультимедийный проектор, экран;
• ПК учащихся.
Методика проведения урока:
Формирование проблемы урока
Задание на соответствие: Даны 2 столбца: «Определения» и «Понятия» Установите между ними соответствие.
| ОПРЕДЕЛЕНИЕ | ПОНЯТИЕ |
| -показывает, какие значения принимает сложное высказывание при всех сочетаниях (наборах) значений входящих в него простых высказываний | Простое высказывание |
| - это выражение, содержащее одну или несколько переменных, соединенных знаками логических операций и скобками и превращающихся в высказывания при подстановке вместо этих переменных простых суждений | Логическая переменная |
| - повествовательное предложение, относительно которого можно сказать истинно оно или ложно | Сложное высказывание |
| - буквы, обозначающие высказывания (А, В,...), ими можно заменить любые высказывания (с любым содержанием). | Таблица истинности |
| - способ построения сложного высказывания из данных высказываний, при котором значение истинности сложного высказывания полностью определяется значениями истинности исходных высказываний. | Логическая функция
|
Объявление темы и цели урока
Сегодня на уроке мы будем строить таблицы истинности, и решать логические задачи с помощью законов математической логики.
Учебные материалы:
Для связи между мыслями используются логические операции, для которых существуют основные законы формальной логики. Таковыми являются законы тождества, коммуникативный, ассоциативный, дистрибутивный.


С целью упрощение сложных высказываний их можно заменить на равносильные на основе законов алгебры высказываний с целью получения высказываний более простой формы. Рассмотрим примеры упрощений.
Пример 1. Требуется упростить: А & В v A & НЕ (В).
По закону дистрибутивности и вынесем А за скобки:
А & В v А & НЕ (В) = А & (В v НЕ(В)) = А & 1 = А.
Пример 2. Требуется упростить: (A v В) & (A v HE (В)).
Применим закон дистрибутивности:
(A v В) & (A v НЕ (В)) = A v (В & НЕ (В)) = A v 0 = А.
Пример 3. Требуется упростить: НЕ(НЕ(Х) ИЛИ НЕ(Y)).
Применим закон де Моргана:
НЕ(НЕ(Х) ν НЕ(У))=НЕ(НЕ(Х)) & НЕ(НЕ(У))=Х & У
Задания для учащихся:
Задание 1.
Найти среди перечисленных сложных суждений противоречащие и эквивалентные:
1. А знает В, но В не знает А.
2. А и В не знают друг друга.
3. Неверно, что А и В не знают друг друга.
4. Тогда как В знает В, А не знает В.
5. Если А знает В, то В знает А.
6. Неверно, что В знает А только тогда, когда А знает В.
7. Неверно, что А знает В или В знает А.
8. А не знает В или В не знает А.
Задание 2.
Пусть а - истинное высказывание, b - ложное высказывание. Определить значение истинности следующих сложных высказываний:
1. (a v b) ⊃ a
2. (a & b) ⊃ a
3. a ⊃ (a & b)
4. a ⊃ (a v b)
5. (a ⊃ b) ⊃ a
6. a ⊃ (b ⊃ a)
7. ~a ⊃ ~(a v b)
8. ~(a ⊃ a & b)
9. (a & ~a) ⊃ b
10. (a ⊃ (b & ~b)) ⊃ ~a
Задание 3.
Упростите логические выражения. Правильность упрощения проверьте с помощью таблиц истинности для исходных и полученных логических формул.
a) A v (НЕ(А)&.В);
б) А &(НЕ(A) v В);
в) (А v В)&( НЕ(В) v А)&(НЕ(С) v В)
г) (1 v (A =B))v((A v C)&1)
Задание 4.
И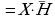
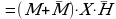
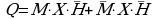 спользуя законы логики упростить выражение:
спользуя законы логики упростить выражение:
1)
2) (AB)+B= A+B+B = A+B
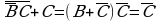
3)
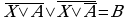
4) Найдите X, если
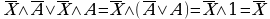
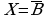
Задание 5.
Какое логическое выражение равносильно выражению ¬ (A / B) / ¬C?
1)¬A / B / ¬C 2)(¬A / ¬B) / ¬C 3)(¬A / ¬B) / C 4)¬A / ¬B / ¬C
Задание 6.
"Прогноз погоды". На вопрос, какая завтра будет погода, синоптик ответил:
-
Если не будет ветра, то будет пасмурная погода без дождя.
-
Если будет дождь, то будет пасмурно и без ветра.
-
Если будет пасмурная погода, то будет дождь и не будет ветра.
Так какая же погода будет завтра?
Решим эту задачу средствами алгебры логики.
Решение:
1. Выделим простые высказывания и запишем их через переменные:
A – «Ветра нет»
B – «Пасмурно»
С – «Дождь»
2. Запишем логические функции (сложные высказывания) через введенные переменные:
Если не будет ветра, то будет пасмурная погода без дождя:
A → B & C
Если будет дождь, то будет пасмурно и без ветра:
С → B & A
Если будет пасмурная погода, то будет дождь и не будет ветра
B → C &
Запишем произведение указанных функций:
F=(A→ B & C) & (C→B & A) & (B→ C & A)
Упростим формулу (используются законы де Моргана, переместительный закон, закон противоречия):
F=(A→ B & ¬C) & (C→B & A) & (B→ C & A)
= (¬A v B & ¬C) & (¬C v B&A) & (¬B v C&A) =
= (¬A v B & ¬C) & (¬B v C&A) & (¬C v B&A) =
= (¬A &¬ B v B&¬C&¬B v ¬A&C&A v B&¬C&C&A) & (C v B&A)=
= ¬A & ¬B &(C v B&¬A) =A&¬B&C v¬ A&¬B&B&¬A =
= ¬A&¬B&¬C
3. Приравняем результат единице, т.е. наше выражение должно быть истинным:F = ¬A &¬ B & ¬C = 1 и проанализируем результат:
Логическое произведение равно 1, если каждый множитель равен 1.
¬A = 1; ¬B = 1; ¬C = 1.значит: A = 0; B = 0; C = 0;
Ответ: погода будет ясная, без дождя, но ветреная.
Задание 7.
«Поход в кино». Рустам, Аня и Мээрим решили пойти в кино. Каждый из них высказал свои пожелания по поводу выбора фильма.
Рустам сказал: «Я хочу посмотреть французский боевик».
Мээрим сказала: «Я не хочу смотреть французскую комедию».
Аня сказала: «Я хочу посмотреть американскую мелодраму».
Каждый из них слукавил в одном из двух пожеланий. На какой фильм пошли ребята?
Решение:
1. Выделим простые высказывания и запишем их через переменные:
А — «Французский фильм»
В — «Боевик»
С — «Комедия»
2. Запишем логические функции (сложные высказывания). Учтем условие о том, что каждый из ребят оказался прав в одном предположении:
а) «Французский боевик» ¬A&B˅A&¬B
б) «Американскую мелодраму» ¬¬A&¬B˅¬ А &¬¬В
в) «Нефранцузская комедия» ¬¬A&C˅¬A&¬C
3. Запишем произведение:
(¬A&B˅A&¬B) & (¬¬A&¬B˅¬ А&¬¬В)&( ¬¬A&C˅¬A&¬C)=1.
Упростим формулу: (¬A&B˅A&¬B) & (¬¬A&¬B˅¬ А&¬¬В)&( ¬¬A&C˅¬A&¬C)=
(¬A&B˅A&¬B) & (A&¬B˅¬ А&В)&( A&C˅¬A&¬C)=
=(¬A&B& A&¬B˅ A&¬B& A&¬B˅¬A&B &¬А&В˅ A&¬B&¬A&B)&( A&C˅¬A&¬C)=
=(A&¬B ˅¬A&B)&( A&C˅¬A&¬C)= A&¬B& A&C˅¬A&B& A&C˅ A&¬B&¬A&¬C˅¬A&B&¬A&¬C= ¬A&B&¬C˅ A&¬B&C =1
6. Составим таблицу истинности для выражения:
¬A&B&¬C˅ A&¬B&C:
| А | В | С | ¬A&B&¬C˅A&¬B&C |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 0 |
|
| 1 | 1 | 1 | 0 |
|
7. Найдем по таблице значения переменных, для которых F=1.
А)
8. Проанализируем результат:
Результат Б) не является решением, т.к. в ответе Мээрим оба утверждения оказываются неверными, что противоречит условию задачи.
Результат А) полностью удовлетворяет условию задачи и поэтому является верным решением.
Ответ: ребята выбрали американский боевик.
Задания из учебника

Решение:
Введем следующие обозначения:
«Это сосуд греческий» — G;
«Это сосуд финикийский» — F;
«Сосуд изготовлен в III веке» — V3;
«Сосуд изготовлен в IV веке» — V4;
«Сосуд изготовлен в V веке» — V5.
Формализуем задачу, записав в данных обозначениях условия задачи.
Со слов учителя следует, что Индира права только в чем-то одном: или G = 1, или V5 = 1.
Таким образом, тождественно истинным будет высказывание: G¬V5 v¬GV5.=1
Аналогично, из слов Эмиля и учителя следует: F¬V3 v ¬FV3 = 1,
а из слов Лены и учителя: ¬G¬V4 v GV4 = 1.
Кроме того, ясно, что сосуд может быть изготовлен только в одном из веков и только в одной из стран. Эти условия можно записать так:
V3¬V4¬V5 ˅ ¬V3V4¬V5 ˅ ¬V3¬V4V5 = 1,
F¬G v ¬FG = 1.
Итак, мы получили пять тождественно истинных высказываний. Их нужно логически перемножить. Результат должен быть также тождественно истинным высказыванием:
1 = (G¬V5 v ¬GV5) & (F¬V3 v ¬FV3) & (¬G¬V4 v GV4) & (F¬G v ¬FG) &(V3¬V4¬V5 ˅ ¬V3V4¬V5 ˅ ¬V3¬V4V5) =
(упростим: сначала перемножим первую и третью скобки и вторую и четвертую скобки)
=(G¬V5¬G¬V4˅¬GV5¬G¬V4 ˅ G¬V5GV4 ˅ ¬GV5 GV4)&( F¬V3F¬G˅¬FV3 F¬G˅ F¬V3 ¬FG ˅ ¬FV3¬FG) & (V3¬V4¬V5 ˅ ¬V3V4¬V5 ˅ ¬V3¬V4V5) =
учитывая, что, G¬G = 0, GG = G,¬ G¬G =¬ G, упростим выражения в первой и второй скобках:
=(¬GV5¬V4 ˅ ¬V5GV4 ) &( ¬FV3G ˅¬V3 F¬G)& (V3¬V4¬V5 ˅ ¬V3V4¬V5 ˅ ¬V3¬V4V5) =
(перемножим первую и вторую скобки и упростим полученное выражение)
(¬GV5¬V4 ¬FV3G˅¬V5GV4¬FV3G˅¬GV5¬V4 ¬V3 F¬G ˅ ¬V5GV4¬V3F¬G) & (V3¬V4¬V5 ˅ ¬V3V4¬V5 ˅ (¬V3¬V4V5)=(¬V5V4¬FV3G˅¬GV5¬V4 ¬V3 F) & (V3¬V4¬V5 ˅ ¬V3V4¬V5 ˅ ¬V3¬V4V5)= ¬GV5¬V4 ¬V3 F¬GV5¬V4 ¬V3 F=1, если ¬G=1, V5=1, ¬V4 =1, ¬V3=1, F=1
Ответ: сосуд финикийский и изготовлен в V веке.
Подведение итогов.
Рефлексия.
-
Какова была цель нашего урока?
-
Достигли ли мы этой цели?
-
Если нет, что помешало?
-
Если да, то, что помогло?








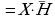
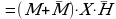
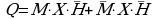 спользуя законы логики упростить выражение:
спользуя законы логики упростить выражение: