Занятие №53 Решение простейших тригонометрических уравнений.

Тригонометрические уравнения

sin x=a, cos x=a, tg x=a, ctg x=a

http://aida.ucoz.ru

Девиз : « Не делай никогда того, чего не знаешь , но научись всему, что следует знать» Пифагор

С помощью тригонометрической окружности найти все значения из промежутка [-2 π ; 2 π ] для следующих выражений

arcsin 0 ,

arcsin

Верно ли равенство

Имеет ли смысл выражение :

Определение .

• Уравнения вида f ( x ) = а , где а – данное число, а f ( x ) – одна из тригонометрических функций, называются простейшими тригонометрическими уравнениями.

Решение простейших тригонометрических уравнений.

Чтобы успешно решать простейшие

тригонометрические уравнения нужно

1) уметь отмечать точки на числовой

окружности ;

2) уметь определять значения синуса, косинуса,

тангенса и котангенса для точек числовой

окружности ;

3) знать свойства основных

тригонометрических функций ;

4) знать понятие арксинуса, арккосинуса,

арктангенса, арккотангенса и уметь отмечать их

на числовой окружности.

17.01.21

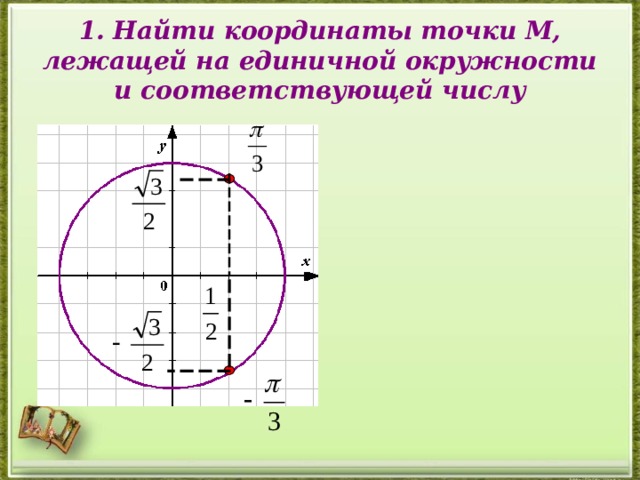
1. Найти координаты точки М, лежащей на единичной окружности и соответствующей числу

2. Дана точка М с абсциссой ½. Найдите ординату этой точки; укажите три угла поворота, в результате которых начальная точка (1;0) переходит в точку М

М

3. Дана точка М с абсциссой - ½. Найдите ординату этой точки; укажите три угла поворота, в результате которых начальная точка (1;0) переходит в точку М

М

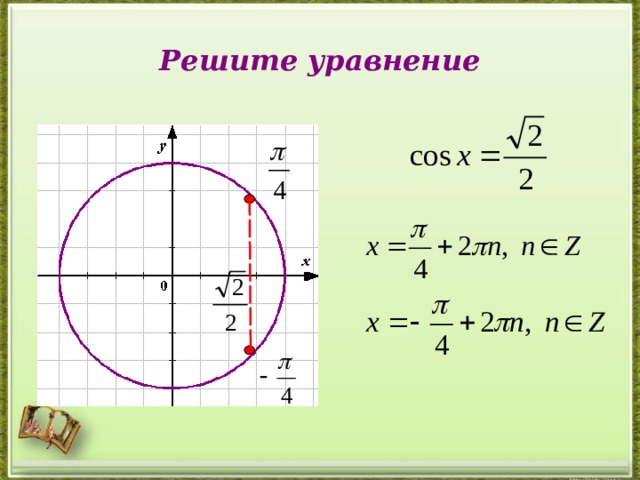
Решите уравнение

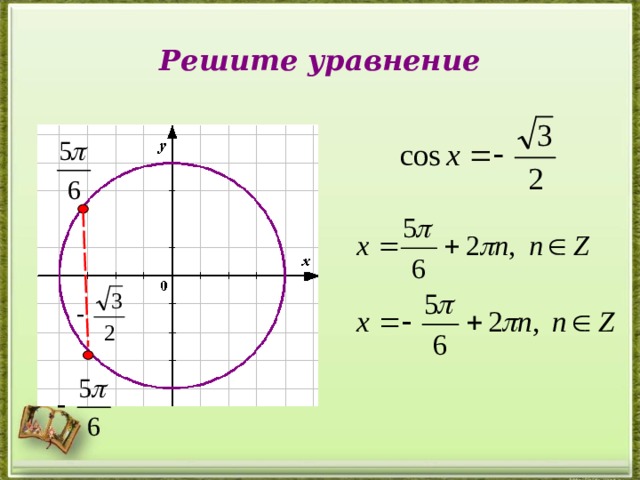
Решите уравнение

у

Арккосинусом числа а называют такое число из промежутка

[0 ; π ] , косинус которого равен а

1

π - arccos a

arccos а

х

0

а

- а

0

π

-1

arccos (-a)= π - arccos a

Решим при помощи

числовой окружности

уравнение cos х = a .

1)

Нет точек пересечения с окружностью.

Уравнение не имеет решений.

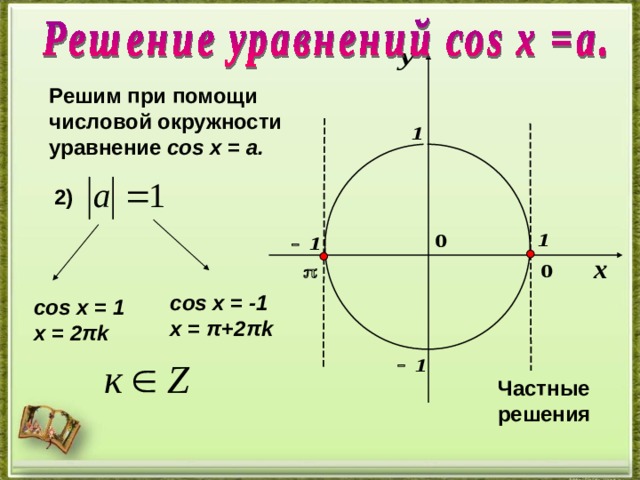
Решим при помощи

числовой окружности

уравнение cos х = a .

2 )

cos х = -1

х = π +2 π k

cos х = 1

х = 2 π k

Частные решения

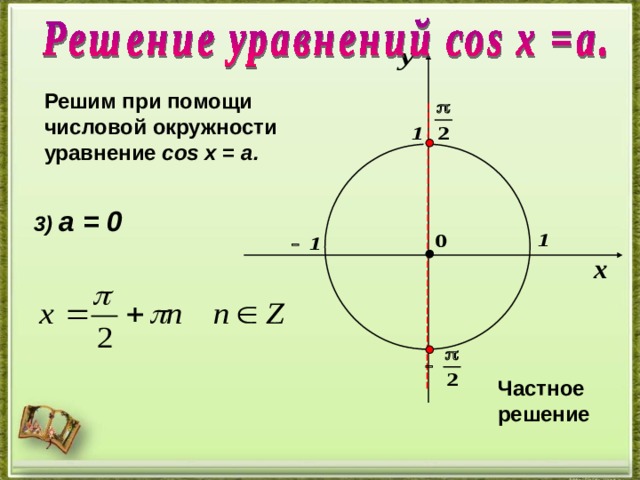
Решим при помощи

числовой окружности

уравнение cos х = a .

3) а = 0

Частное решение

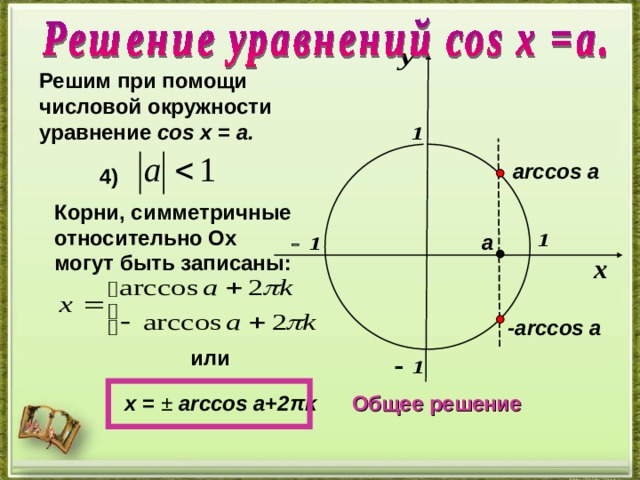
Решим при помощи

числовой окружности

уравнение cos х = a .

arccos а

4 )

Корни, симметричные относительно О x могут быть записаны :

а

- arccos а

или

х = ± arccos a+2 π k

Общее решение

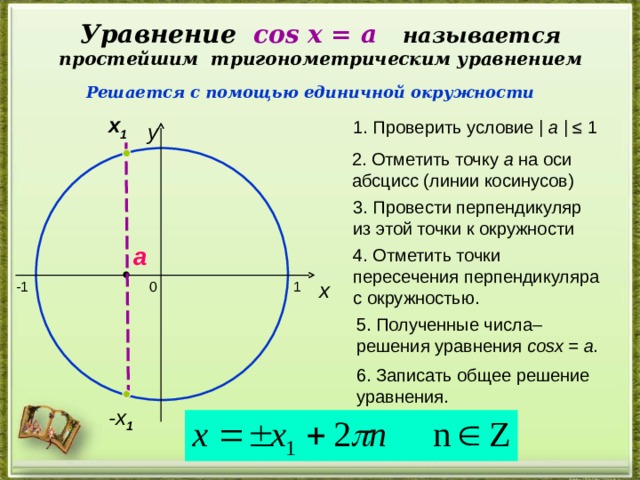
Уравнение cos х = a называется простейшим тригонометрическим уравнением

Решается с помощью единичной окружности

х 1

1 . Проверить условие | a | ≤ 1

y

2 . Отметить точку а на оси абсцисс (линии косинусов)

3 . Провести перпендикуляр из этой точки к окружности

a

4 . Отметить точки пересечения перпендикуляра с окружностью .

x

0

-1

1

5 . Полученные числа– решения уравнения cos х = a.

6 . Записать общее решение уравнения .

- х 1

1 и a " width="640"

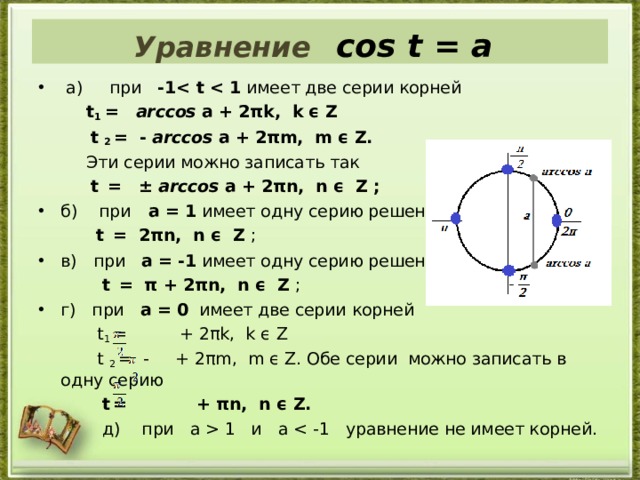
Уравнение cos t = a

• a ) при -1 t имеет две серии корней

t 1 = ar с cos a + 2πk, k ϵ Z

t 2 = - ar с cos a + 2πm, m ϵ Z.

Эти серии можно записать так

t = ± ar с cos a + 2πn, n ϵ Z ;

• б) при а = 1 имеет одну серию решений

t = 2 πn , n ϵ Z ;

• в) при а = -1 имеет одну серию решений

t = π + 2 πn , n ϵ Z ;

• г) при а = 0 имеет две серии корней

t 1 = + 2 πk , k ϵ Z

t 2 = - + 2 πm , m ϵ Z . Обе серии можно записать в одну серию

t = + πn , n ϵ Z .

д) при а 1 и a

Решите уравнение

1) cos х =

2 ) cos х = -

Решите уравнение

3) cos 4x = 1

4x = 2πn, n ϵ Z

4)

Решите уравнение

.

5)

1 и a уравнение не имеет корней. " width="640"

Уравнение sin t = a

• a ) при -1 t имеет две серии корней

t 1 = ar с sin a + 2πn, n ϵ Z

t 2 = π - ar с sin a + 2πn, n ϵ Z.

Эти серии можно записать так

t = ( -1) k ar с sin a + πk , k ϵ Z ;

• б) при а = 1 имеет одну серию решений

t = + 2 πn , n ϵ Z

• в) при а = -1 имеет одну серию решений

t = - + 2 πn , n ϵ Z ;

• г) при а = 0 имеет две серии корней

t 1 = 2 πk , k ϵ Z ,

t 2 = π + 2 πm , m ϵ Z .

Обе серии можно записать в одну серию

t = πn , n ϵ Z ;

• д) при а 1 и a уравнение не имеет корней.

Решите уравнение

,

,

• sin х =

+ πk , k ϵ Z .

x = ( -1) k

( -

;

Решите уравнение

,

;

,

2) sin х = -

x = ( -1) k +1

x = ( -1) k ( -

+ πk , k ϵ Z

+ πk , k ϵ Z

Задание 2. Найти корни уравнения:  

1) a) sin x =1 б ) sin x = - 1 в ) sin x = 0

г ) sin x =1,2 д ) sin x = 0,7

2) а) б)

в) г)

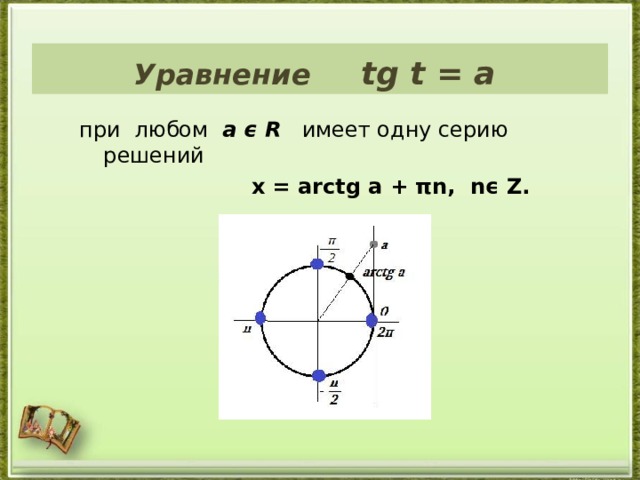
Уравнение tg t = a

при любом а ϵ R имеет одну серию решений

х = а rctg a + πn, nϵ Z.

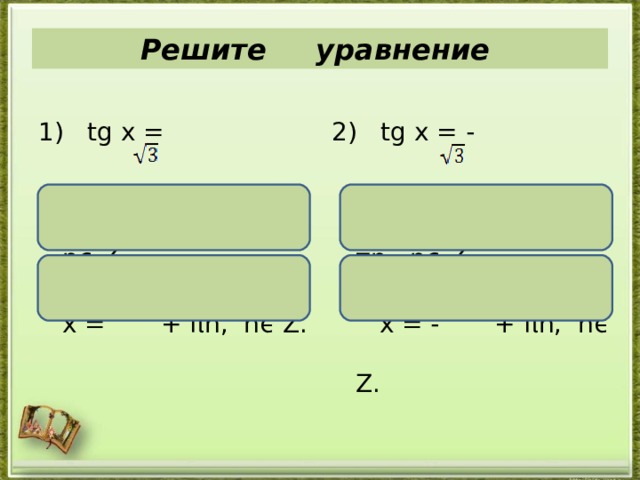
Решите уравнение

2) tg x = -

х = а rctg (- ) + πn, nϵ Z,

x = - + πn , nϵ Z .

1 ) tg x =

х = а rctg + πn, nϵ Z.

x = + πn, nϵ Z.

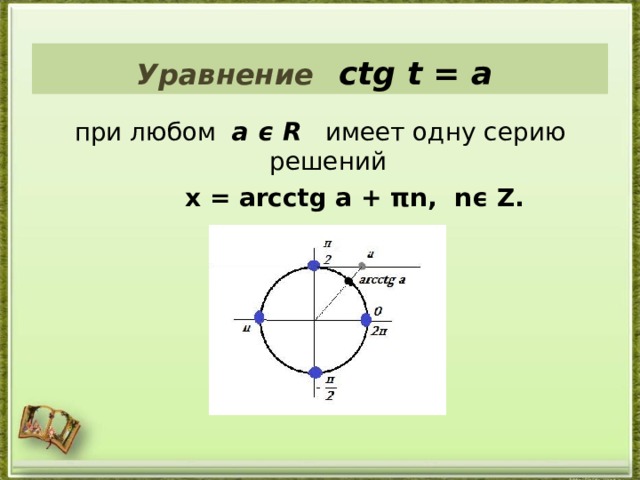
Уравнение ctg t = a

при любом а ϵ R имеет одну серию решений

х = а rcctg a + πn, nϵ Z.

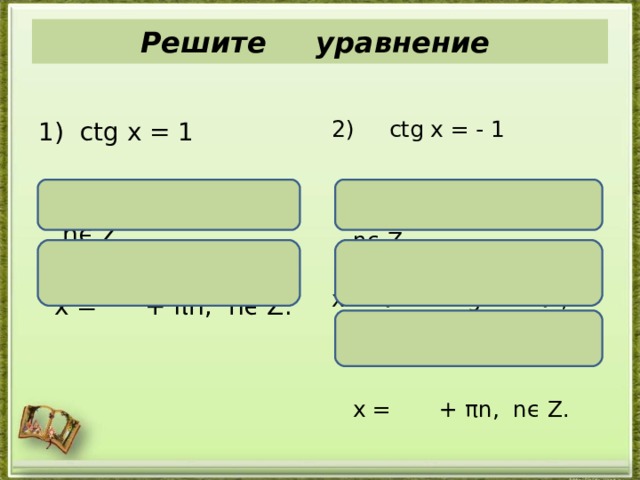
Решите уравнение

1) ctg x = 1

 

х = а rcctg 1 + πn, nϵ Z,

х = + πn , nϵ Z .

2) ctg x = - 1

х = а rcctg ( -1) + πn , nϵ Z

х = π - а rcctg 1 + πn , nϵ Z

х = + πn , nϵ Z .

1 | a|Ø sin x = a tg x = a x=±arccos a+2 π n a =1 Ø ctg x = a x=arctg a + π n x=(-1)ⁿarcsin a+ π n x=2 π n a = -1 x= π +2 π n x=arcctg a + π n x=arctg a + π n x= π/2+ 2 π n a = 0 x=- π/2+ 2 π n x= π/ 4 +π n x=arcctg a + π n x= π/2+π n x= π/ 4 +π n x=- π/ 4 +π n x= π n x=3 π/ 4 +π n x= π n x= π/2+π n " width="640"

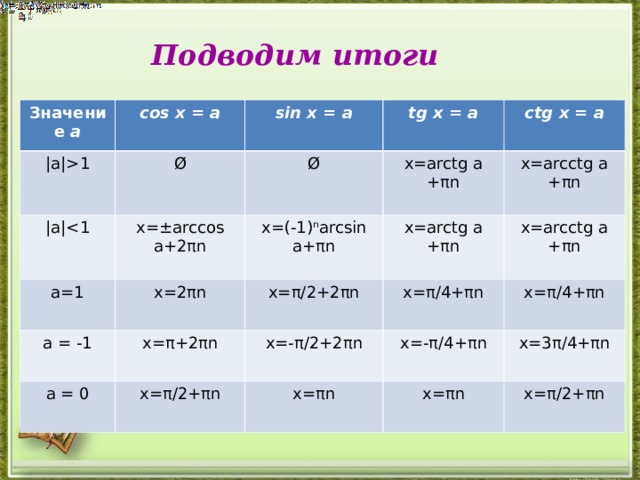
Подводим итоги

Значение а

cos x = a

| a|1

| a|

Ø

sin x = a

tg x = a

x=±arccos a+2 π n

a =1

Ø

ctg x = a

x=arctg a + π n

x=(-1)ⁿarcsin a+ π n

x=2 π n

a = -1

x= π +2 π n

x=arcctg a + π n

x=arctg a + π n

x= π/2+ 2 π n

a = 0

x=- π/2+ 2 π n

x= π/ 4 +π n

x=arcctg a + π n

x= π/2+π n

x= π/ 4 +π n

x=- π/ 4 +π n

x= π n

x=3 π/ 4 +π n

x= π n

x= π/2+π n

Вы молодцы!

Каждый из вас «научись тому, что следует знать».

Спасибо за урок !