| № и название этапа | Деятельность учителя | Деятельность учащихся |
| 1.Организационный этап | -Здравствуйте, ребята. Сегодня замечательный день. Светит солнце, улыбается нам, и вы улыбнитесь друг другу. У нас сегодня гости, они желают вам всего хорошего, активной работы и верных решений. Садитесь. | Ребята готовы к уроку, садятся. |
| 2. Актуализация знаний | Давайте проверим домашнее задание. У кого возникли вопросы? Какой номер вызвал затруднение? Проверим решение. Графики каких функций получились в первом задании? 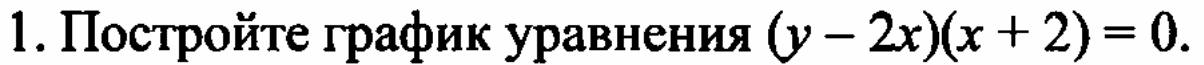 Назовите ответ второго задания 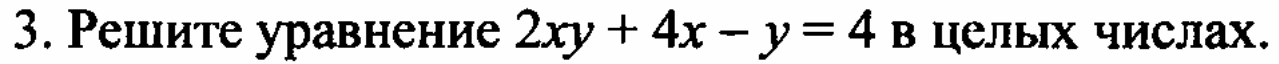
| Отвечают на вопрос
У = 2х, х = -2
(0;-4), (1;0) |
| 3. Основной этап | -Давайте вспомним, что мы делали на предыдущем уроке? -А что значит решить уравнение?
-Как записывается ответ при решении уравнений с двумя переменными? -В каких темах курса алгебры вы решали вопрос о нахождении значения двух переменных, которые удовлетворяют заданным условиям? - Именно так звучит тема нашего урока. Откройте тетради, запишите число, тема урока «Системы уравнений». (записывает на доске) | -Решали уравнения с двумя переменными -Найти его корни или доказать, что корней нет -В виде пары значений
-решение систем уравнений
Делают записи в тетради
|
| Целепологание | - Системы уравнений вам знакомы с 7 класса. И ваши знания расширялись с появлением новых видов уравнений. Тогда какова цель нашего сегодняшнего урока?
| - Вспомнить методы решения систем уравнений. Учиться выбирать рациональный метод |
|
| -Начнем вспоминать. 1. Определение (на слайде) -Как называют такую пару чисел? -Что значит решить систему уравнений? -Также можно говорить и о системах с любым количеством уравнений. Тогда решение будут тройки, четверки и т.д., удовлетворяющие каждому уравнению -Чтобы говорить о решении системы, давайте посмотрим, что система состоит из уравнений, а решая уравнение мы переходим к более простому с помощью равносильных преобразований. -Значит, стоит говорит и о равносильности систем. -Как вы думаете, какие системы называются равносильными? (слайд)
-Какие методы решения систем уравнений вы знаете? -Все эти методы приводят к равносильным системам, но если в процессе решения уравнений вы использовали неравносильные преобразования, то требуется проверка. |
-решением системы -ответ
-переход к более простому
-системы, которые имеют одни и те же решения или не имеют их
-Метод сложения, подстановки, геометрический, замены переменных |
| Решение задач | Перейдем к решению. Работать будем в парах. У каждого на парте лежит конверт, в нем 8 систем уравнений. Ваша задача рассортировать эти системы по методу решения и наметить план. Работаем 3 минуты.
-Время вышло. Приступим к обсуждению методов и решению систем. -С какого метода начнем?
-Давайте вспомним алгоритм использования данного метода.
Какая пара готова продемонстрировать решение системы, для которой данный метод рациональнее остальных? Как выполнить проверку?
Аналогичная работа проводится для каждого метода | Работают в паре, осуществляют сортировку.
Называют метод решения системы уравнений Перечисляют шаги (появляется слайд с алгоритмом)
Один учащийся показывает решение
Подставить значения в каждое уравнение |
| Физкультминутка (после решения первой системы) | Учитель проводит динамическую паузу. Упражнения для глаз, рук, ног, туловища (После зарядки) Итак. Еще раз. Система уравнений может содержать 2 и более уравнений, решением является пара, тройка и т.д. чисел. При решении выбирается рациональный метод: сложения, подстановки, замены переменных, графический. В конце выполняется проверка.
| Выполняют упражнения. |
| Проблемная ситуация | 
Обсудите решение в паре. (1 минута)
-Огласите ваши идее по решению. (если затрудняются задаются наводящие вопросы) -Сколько раз каждая переменная входит в систему? Какой метод можно применить? -какое выражение получится, если применить метод сложения для всех уравнений?(выполните в тетрадях) -Что сделаем дальше?
-Можно ли выделить эту группу слагаемых в каждом уравнении? -Выполните замену | Обсуждают решение
Называют возможные способы решения
-Сложения
4х+4у+4z = 8
Сократим на 4 Получится x+y+z = 2
-да x+2 = 1, x = -1 2+y = 3, y = 1 2+z = 4, z = 2 (-1,1,2) |
| 4. Подведение итогов, домашнее задание, рефлексия | - Обратимся к цели урока. Вспомнить методы решения систем уравнений. Учиться выбирать рациональный метод решения
- Как вы считаете, она достигнута?
-Запишите домашнее задание (4 уравнения, на разные методы решения) №59.1а, 59.3а, 59.5а, 59.8а
-Если вы покидаете класс с хорошим настроением - похлопайте в ладоши, а если с плохим - потопайте |
-Ответы детей.
Записывают домашнее задание в дневник
Демонстрируют свое настроение |


















