№ 3 для 9-А Объем тела. Свойства прямоугольного параллелепипеда

7.04.20. 9 –А класс Урок № 3

Тема: Объем тела. Свойства прямоугольного параллелепипеда

Цели: повторить понятие площади, ввести понятие объема тела, изучить основные свойства объемов и прямоугольного параллелепипеда; познакомиться с принципом Кавальери.

Скачивайте файл, чтобы не терять данные

1. Организационный урок

Здравствуйте, продолжаем изучение основ стереометрии. Читаем, рисуем, конспектируем

2. Актуализация

Повторяем  понятие площади плоской фигуры:

(площадью фигуры называется положительная величина, определённая для каждой фигуры так, что:

1) равные фигуры имеют равные площади;

2) если фигура состоит из двух частей, то её площадь равна сумме площадей этих частей).

Еще раз идем по ссылке: смотрим, вспоминаем, задаем вопросы:

https://www.yaklass.ru/ЯКЛАСС дистанционный тренинг для школьников до темы Пирамида.

https://www.youtube.com/watch?v=BHd7XLjAbro 10 класс, 30 урок, Призма
https://www.youtube.com/watch?v=WJ71Vrs1U-M Призма | Геометрия 7-9 класс #119 | Инфоурок

https://www.youtube.com/watch?v=khl8j_F8Ytg Геометрия 10 кл Призма
https://www.youtube.com/watch?v=QbpZp0ecmFM Математика 5 класс. Прямоугольный параллелепипед
https://www.youtube.com/watch?v=OAF9Xv3oRYk 9 класс, 37 урок, Параллелепипед

ПРОВЕРЯЕТСЯ. Сможете ли вы решить данную проверочную? Хватит ли у вас знаний, если возникнуть проблемы, напишите, какая тема вам оказалась не под силу. Почему?

1. Найдите объём куба, со стороной 4 см.

2. Найдите общую длину рёбер куба, если длина одного его ребра равна 17 дм.

3. Найдите площадь поверхности прямоугольного параллелепипеда, если его измерения равны 2 см, 7 см, 8 см.

4. Бассейн, имеющий форму прямоугольного параллелепипеда, имеет длину 6 м, ширину 2 м и высоту 1 м. Бассейн наполнен водой до его высоты. Найдите объём воды, налитой в бассейн.

5.Общая длина рёбер прямоугольного параллелепипеда 712 см. Первое ребро на 18 см больше второго, а второе в два раза больше третьего. Найдите рёбра параллелепипеда.

3. Изучение нового материала.

Понятие объема тела вводится по аналогии с понятием площади плоской фигуры. За единицу измерения объемов примем куб, ребро которого равно единице измерения отрезков. Куб с ребром 1 см называется кубическим сантиметром и обозначается так: 1 см³. Аналогично определяются кубический метр (м³), кубический миллиметр (мм³) и т. д.

Прочитать по учебнику текст (с. 306 и 307) и записать в тетрадях основные свойства объемов:

1) Равные тела имеют равные объемы.

2) Если тело составлено из нескольких тел, то его объем равен сумме объемов этих тел (рис. 347):

V = V₁ + V₂.

Разобрать по рисунку учебника (рис. 348) принцип Кавальери.

Когда мы говорим о размерах комнаты, имеющей форму прямоугольного параллелепипеда, то обычно употребляем слова «длина», «ширина» и «высота», имея в виду длины трех ребер с общей вершиной. В геометрии эти три величины объединяются общим названием: измерения прямоугольного параллелепипеда (рис. 349, с. 317 учебника).

У прямоугольника два измерения – длина и ширина. При этом, как мы знаем, квадрат диагонали прямоугольника равен сумме квадратов двух его измерений (по теореме Пифагора для прямоугольника). Оказывается, что аналогичным свойством обладает и прямоугольный параллелепипед: квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений. (Используя рисунок 349, провести доказательство этого свойства).

Доказательство записывать в тетрадях:

АС₁² = АС² + СС₁²;

АС² = АВ² + АD²;

СС₁ = ВВ₁ = АА₁,

следовательно, АС₁² = АВ² + АD² + АА₁².

Еще одно свойство прямоугольного параллелепипеда. Мы знаем, что площадь прямоугольника равна произведению его измерений. Аналогично объем прямоугольного параллелепипеда равен произведению трех его измерений.

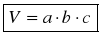
Для доказательства этого утверждения воспользуемся принципом Кавальери (прочитать доказательство по учебнику на с. 317–319, используя рисунок 350).

В прямоугольном параллелепипеде с измерениями a, b, c, изображенном на рисунке учебника (рис. 350, б), площадь S основания равна ас, а высота h равна боковому ребру: h = b.

Поэтому формулу V = a ∙ b ∙ c можно записать в виде

,

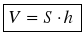то есть объем прямоугольного параллелепипеда равен произведению площади основания на высоту.

Закрепление. Делаем записи в тетради

1. Решить задачу № 1193 (б; в).

№ 1193 (в) в тетрадях.

Решение

a = 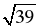 ; b = 7; с = 9. Найти диагональ d.

d² = a² + b² + c²

(свойство диагонали прямоугольного параллелепипеда).

d² = (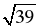 )² + 7² + 9² = 39 + 49 + 81 = 169;

d =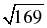 = 13.

Ответ: 13.

2.Решить задачу № 1193 (б) .

Решение

а = 8; b = 9; с = 12. Найти d.

d² = a² + b² + c²

d ²= 8² + 9² + 12² = 64 + 81 + 144 = 289;

d₁ =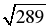 = 17;

d₂ = –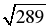 = –17 не удовлетворяет условию задачи.

Ответ: 17.

3. Решить задачу № 1194 в тетрадях.

Решение

Ребро куба равно а. Найти диагональ этого куба.

d² = a² + a² + a² = 3a²;

d = 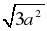 = a .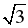

Ответ: a .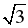

Решение

4. Разобрать по учебнику решение задачи № 1198 (с. 323, используя рис. 357).

Записать в тетрадях: «Объем призмы равен произведению площади основания на высоту».

.

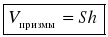5. Решить задачу № 1197.

.

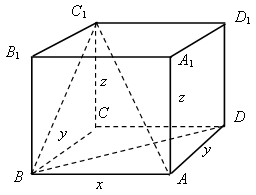
Решение

АС₁ = 13 см; ВD = 12 см; ВС₁ = 11 см.

Обозначим измерения прямоугольного параллелепипеда x, y, z.

Применим теорему Пифагора:

1) Для Δ АВD имеем

х² + y² = 12². (1)

2) Для Δ ВСС₁ имеем

y² + z² = 11². (2)

3) По свойству диагонали прямоугольного параллелепипеда имеем

х² + у² + z² = 13². (3)

4) Подставим в равенство (3) равенство (1), получим 12² + z² = 13²,

отсюда z² = 13² – 12²,

тогда z =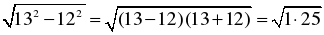 = 5;

z = 5.

5) Подставим в равенство (2) значение z = 5, найдем

y² + 5² = 11²;

у² = 121 – 25 = 96;

_;

_{= .}

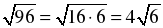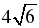6) Подставим значение y² = 96 в равенство (1), получим

х² + 96 = 144;

х² = 144 – 96 = 48;

;

.

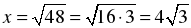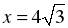7) Найдем объем

V = x ∙ y ∙ z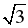 = 4 ∙ 4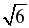 ∙ 5 = 80 =
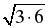= 80= 80= 240(см³).

Ответ: 240см³.

4. Домашняя работа.

п. 122–123; сделать чертеж (рис. 357) и записать в тетрадях решение задач № 1193 (а), 1196, 1198.